- Research Article
- Open access
- Published:
Multiresolution Source/Filter Model for Low Bitrate Coding of Spot Microphone Signals
EURASIP Journal on Audio, Speech, and Music Processing volume 2008, Article number: 624321 (2008)
Abstract
A multiresolution source/filter model for coding of audio source signals (spot recordings) is proposed. Spot recordings are a subset of the multimicrophone recordings of a music performance, before the mixing process is applied for producing the final multichannel audio mix. The technique enables low bitrate coding of spot signals with good audio quality (above 3.0 perceptual grade compared to the original). It is demonstrated that this particular model separates the various microphone recordings of a multimicrophone recording into a part that mainly characterizes a specific microphone signal and a part that is common to all signals of the same recording (and can thus be omitted during transmission). Our interest in low bitrate coding of spot recordings is related to applications such as remote mixing and real-time collaboration of musicians who are geographically distributed. Using the proposed approach, it is shown that it is possible to encode a multimicrophone audio recording using a single audio channel only, with additional information for each spot microphone signal in the order of 5 kbps, for good-quality resynthesis. This is verified by employing both objective and subjective measures of performance.
1. Introduction
Multichannel audio offers significant advantages regarding music reproduction when compared to two-channel stereo audio. (In the following, when we are referring to stereo audio, we always mean two-channel stereo.) The use of a large number of channels around the listener results in a more realistic acoustic space, adding more sound directions, and thus immersing the listener into the acoustic scene. By using a higher number of channels than in stereo systems, multichannel audio recordings require higher datarates for transmission. Stereo and multichannel audio coding methods attempt to significantly reduce the datarates of audio recordings for networked audio applications or for relaxing their storage requirements. This paper focuses on reducing the transmission (and storage) requirements of spot microphone signals (before those are mixed into the final multichannel audio mix), by exploiting the similarities between such signals of the same multimicrophone recording.
MPEG-1 audio coding [1, 2] (including the popular Layer III also known as MP3 audio coding), MPEG-2 AAC (advanced audio coding) [3–5], and Dolby AC-3 [6, 7] are some well-known audio coding methods for stereo and multichannel audio content. These methods mainly exploit the masking property of the human auditory system for shaping the quantization noise so that it will be inaudible. In addition to reducing the intrachannel redundancies and irrelevancies, these methods also include algorithms for exploring the interchannel redundancies, irrelevancies, more specifically mid/side coding [8], for frequencies below 2 kHz, and intensity stereo coding [9] above 2 kHz. M/S codes the sum and difference signals instead of the actual channels, operating in an approximate Karhunen-Loeve (K-L transform) manner. Intensity stereo is based on coding only the sum signal of the channels, as well as the time envelopes for each channel as side information, given that these envelopes are adequate for synthesizing the spatial image at the decoder. A useful introduction to several technologies for the more general area of audio compression can be found in [10]. More recently, exact KLT methods have been derived (e.g., [11]), while intensity stereo has been generalized for the entire frequency spectrum by MPEG Surround [12].
With the exception of MPEG Surround, the above-mentioned multichannel audio coding algorithms result in datarates which remain highly demanding for many practical applications when the available channel bandwidth is low. This is especially important given the fact that possibly future multichannel audio systems will require more than the 5.1 channels of currently popular formats [13] and thus even higher datarates. In MPEG Surround, the concept of spatial audio coding (SAC) has been introduced with the objective of further taking advantage of interchannel redundancies and irrelevancies in multichannel audio recordings. Under this approach, the objective is to decode an encoded downmix (monophonic) channel of audio using some additional (side) information, so as to recreate the spatial rendering of the original multichannel recording. The side information is extracted during encoding and includes the cues which are necessary for synthesizing the spatial image of the uncompressed multichannel audio recording. MPEG Surround is based on combining two theoretical approaches on SAC, namely, binaural cue coding (BCC) and parametric stereo (PS). In BCC [14, 15], the side information contains the per subband interchannel level difference, time difference, and correlation. The resulting signal contains one channel of audio (downmix) only, along with the side information with bitrate in the order of few kbps per channel. Parametric stereo (PS) [16], operates in very similar philosophy.
At a point where MPEG Surround achieves coding rates for 5.1 multichannel audio that are similar to MP3 coding rates for 2-channel stereo, it seems that the research in audio coding might have no future. However, this is far from the truth. Current multichannel audio formats will eventually be substituted by more advanced formats. Future audiovisual systems will not distinguish between whether the user will be watching a movie or listening to a music recording; audiovisual systems of the future are envisioned to offer a realistic experience to the user who will be immersed into the content. Thus immersive audio focuses on applications where the environment of the listener will be seamlessly transformed into the environment of his/her desire. Immersive audio, as opposed to multichannel audio, is based on providing the listener the option to interact with the sound environment. This interactivity can be accomplished when the content can be dynamically modified, which in practice is possible only when the decoder has access to the microphone signals and locally creates the final mix (remote mixing). We note that these microphone signals are the recordings captured by the various microphones that are placed in a venue for recording a music performance. The number of these microphone signals is usually higher than the available loudspeakers, thus a mixing process is needed when producing a multichannel audio recording. As mentioned, remote mixing is imperative for immersive audio applications, since it offers the amount of freedom for the creation of the content that is needed for interactivity. Consequently, in this paper, the focus is on the spot microphone signals of a multimicrophone recording, before those that are mixed into the final multichannel audio mix. In Section 2, useful information about the recording process for multichannel audio and about the particular type of those signals that are examined here (spot signals) is given.
In order to better explain the emphasis on remote mixing, we briefly mention some possible immersive audio applications, such as (network-based) telepresence of a user in a concert hall performance in real time, where interactivity would translate into him/her being able to move around in the hall and appreciate the hall acoustics. In practice, (when the user is not an experienced audio engineer) this could be accomplished by storing at the decoder a number of predefined mixing "files" that have been created by experts for each specific recording. Another application of interest is virtual music performances, where the musicians are located all around the world. Consider for simplicity a scenario where half members of an orchestra are located in one venue and half at another venue. For producing the multichannel audio mix, the spot signals must be first transmitted to a central location where the audio engineer will have access to all individual recordings. More generally, access to spot signals is important in remote collaboration of geographically distributed musicians, which is a field of significance with extensions to music education and research. Current experiments have shown that high datarates are needed so that musicians can perform and interact with minimal delay [17]. Remote mixing is also a central component in collaborative environments for the production of music, which is of importance in the audio engineering community.
The model proposed in this paper is a source/filter representation of spot microphone signals, allowing for transmission of the multiple microphone signals of a music performance with moderate datarate requirements. This would allow for transmission through low bandwidth channels such as the current Internet infrastructure or wireless networks for broadcasting. The proposed model is tailored towards the transmission of the various microphone signals of a performance before they are mixed and thus can be applied to applications such as remote mixing and distributed performances. Our approach relaxes the current bandwidth constraints of these demanding applications, enabling their widespread usage and more clearly revealing their value. Our method operates in similar philosophy as spatial audio coding, that is, it reduces a multichannel recording into a single audio channel (which can be a sum of the multiple microphone signals) and some side information of the order of few kbps per channel. However, the focus on spot signals instead of the audio channels after the mixing process is a clear distinction between these two methods. In SAC, the side information can be used to recreate the spatial rendering of the various channels. In our method, the side information focuses on encoding the microphone signals of the multichannel recording. This is due to the fact that, for audio mixing (remote or not), not only the spatial image (as in SAC, including the "flexible rendering" approach of BCC) but the actual content of each (monophonic) microphone recording must be encoded, so that the audio engineer will have full control on the available content. Our algorithm results in bitrates of the same order with SAC, while being able to encode an approximate version of each mono spot signal. We note that, as in SAC, the single wideband audio channel, that needs to be transmitted for our algorithm, can be encoded using any existing method of monophonic audio compression (e.g., using perceptual audio coders). We also note our focus in low bitrate coding applications. Our objective is to obtain subjective results above 3.0 perceptual grade compared to the original recording, which can be considered a good performance for low bitrate coding applications.
The remainder of this paper is organized as follows. In Section 2, a brief overview is given on how recordings are made for multichannel rendering, with emphasis on concert hall performances. In Section 3, the theoretical background for the model used and the motivation behind the choice of this particular model are provided. In Section 4, it is explained how the derived model parameters can be encoded for transmission, based on previous work of [18] derived for coding of speech LSF parameters. In Section 5, objective and subjective results are provided for both the model and coding performance (emphasis on the modeling rather than the coding method), which show that the proposed algorithm can produce good-quality audio resynthesis with rates of only 5 kbps per microphone signal. Finally, concluding remarks are made in Section 6.
2. Recording for Multichannel Audio
Before proceeding to the description of the proposed method, a brief description is given of how the multiple microphone signals for multichannel rendering are recorded. In this paper, we mainly focus on live concert hall performances, although this does not result in a loss of generality of our methods as we show in Section 5. A number of microphones are used to capture several characteristics of the venue, resulting in an equal number of microphone signals (stem recordings). These signals are then mixed and played back through a multichannel audio system. Our objective is to design a system based on available microphone signals, that is able to recreate all of these target microphone signals from a smaller set (or even only one, which can be the sum of all microphone signals) of reference microphone signals at the receiving end. The result would be a significant reduction in transmission requirements, while enabling remote mixing at the receiving end. In our previous work [19], we were interested to completely synthesize the target signals using the reference signals, without any additional information. Here we propose using some additional information for each microphone for achieving good-quality resynthesis (above 3.0 perceptual grade compared to the original), with the constraint that this additional information requires minimal datarates for transmission. By examining the acoustical characteristics of the various stem recordings, the distinction of microphones is made into reverberant and spot microphones.
Spot microphones are microphones that are placed close to the sound source. Because the source of sound is not a point source but rather distributed such as in an orchestra, the recordings of these microphones depend largely on the instruments that are near the microphone and not so much on the hall acoustics. Resynthesizing the signals captured by these microphones, therefore, involves enhancing certain instruments and diminishing others, which in most cases overlap in the time and frequency domains. Reverberant microphones are the microphones placed far from the sound source, that mainly capture the reverberation information of the venue. In our earlier work [19], we showed that the reverberant recordings can be resynthesized from a reference recording using specially designed LTI filters. Here we focus on the spot microphone signals. Our objective is to design a system that recreates these signals from a smaller subset of the microphone recordings, with minimal error. We note that the methods proposed in this paper are based on our previous work in multichannel audio synthesis [20] and resynthesis [19].
In order to achieve audio compression, especially in low bitrate applications which is the case in this paper, it is generally accepted to introduce an amount of distortion to the coded signals. Here, the distortion corresponds to an amount of crosstalk that is introduced during encoding. We consider that in many applications, a small amount of crosstalk is more acceptable than a considerable degradation in quality. As we showed in later sections, the amount of crosstalk introduced by our methods is small, while the quality remains good for low bitrate applications. In order to better explain the nature of the introduced crosstalk, a simple example is given. If a microphone was placed, for example, near the chorus of an orchestra, then the main objective of the microphone placement is to capture a recording of the music where the chorus sounds as the most prevailing part with respect to the remaining parts of the orchestra. If this microphone signal is substituted by a different (i.e., resynthesized) one, which again contains the same performance and the chorus is the prevailing part of the new signal, this is considered as a signal that retains the "objective" of the initial microphone signal. Crosstalk refers to the case when in the resynthesized signal, apart from the chorus, other parts of the orchestra might be now more audible than in the initial signal. Subjectively, this will have the effect that the new signal sounds as if it was captured by a microphone that was placed farther from the chorus compared with the microphone placement of the original recording. However, given that the amount of crosstalk is small, the chorus will remain the most prominent part in the recording and the resynthesized signal will still sound as if it was made with a microphone placed close to the chorus. The crosstalk is introduced since in our model all spot signals are resynthesized based on a single reference recording.
3. Spot Signals Modeling
The proposed methodology, which is based on a multiband source/filter representation of the multiple microphone signals, consists of the following steps. Each microphone signal is segmented into a series of short-time overlapping frames using a sliding window. For each frame, the audio signal is considered approximately stationary, and the spectral envelope is modeled as a vector of linear predictive (LP) coefficients, using autocorrelation analysis [21]. The resulting vector contains the coefficients of an all-pole filter that approximates the spectral envelope of the audio signal at the particular frame. The modeling error is the result of inverse filtering the audio frame with the estimated LP filter. Below, a brief review of the mathematical background for the source/filter model is given, which will be useful for explaining our approach later in this section. For this purpose, we view the source/filter model from a spectral estimation perspective. Thus we start by considering a single audio frame and its spectrum is modeled by a vector of few coefficients, for reducing the information flow of the audio signal. Linear predictive analysis is employed, resulting in an all-pole filter, practically with much less coefficients than the samples of the audio frame. Under the source/filter model, the signal  at time
at time  is related to the
is related to the  previous signal samples by the following autoregressive (AR) equation
previous signal samples by the following autoregressive (AR) equation

where  is the modeling error, and
is the modeling error, and  is the AR filter order. In the frequency domain, this relation can be written as
is the AR filter order. In the frequency domain, this relation can be written as

where  and
and  denote the power spectrum of signals
denote the power spectrum of signals  and
and  respectively.
respectively.  denotes the frequency response of the AR filter, that is,
denotes the frequency response of the AR filter, that is,

The  th-dimensional vector
th-dimensional vector  is the low-dimensional representation of the signal spectral properties. If
is the low-dimensional representation of the signal spectral properties. If  is an AR process, the noise
is an AR process, the noise  is white, thus
is white, thus  completely characterizes the signal spectral properties. In the general case, the error signal (or residual signal) will not have white noise statistics and thus cannot be ignored. In this general case, the all-pole model that results from the LP analysis gives only an approximation of the signal spectrum, and more specifically the spectral envelope. For the particular case of audio signals, the spectrum contains only the frequency components that correspond to the fundamental frequencies of the recorded instruments and all their harmonics. (For simplicity, at this point we consider only harmonic sounds. The proposed model is tested for complex music signals in Section 5.) The AR filter for an audio frame will capture its spectral envelope. The error signal is the result of the audio frame filtered with the inverse of its spectral envelope. Thus we conclude that the error signal will contain the same harmonics as the audio frame, but their amplitudes will now have significantly flatter shape in the frequency spectrum.
completely characterizes the signal spectral properties. In the general case, the error signal (or residual signal) will not have white noise statistics and thus cannot be ignored. In this general case, the all-pole model that results from the LP analysis gives only an approximation of the signal spectrum, and more specifically the spectral envelope. For the particular case of audio signals, the spectrum contains only the frequency components that correspond to the fundamental frequencies of the recorded instruments and all their harmonics. (For simplicity, at this point we consider only harmonic sounds. The proposed model is tested for complex music signals in Section 5.) The AR filter for an audio frame will capture its spectral envelope. The error signal is the result of the audio frame filtered with the inverse of its spectral envelope. Thus we conclude that the error signal will contain the same harmonics as the audio frame, but their amplitudes will now have significantly flatter shape in the frequency spectrum.
Consider now two microphone signals of the same music performance, which have been placed close to two different groups of instruments of the orchestra. Each of these microphones mainly captures that particular group of instruments but also captures all the other instruments of the orchestra. For simplification, consider that the orchestra consists of only two instruments, that is, a violin and a trumpet. Microphone 1 is placed close to the violin and microphone 2 close to the trumpet. It is true in most practical situations, that microphone 1 will also capture the trumpet, in much lower amplitude than the violin and vice versa for microphone 2. In that case, the signal  from microphone 1 and the signal
from microphone 1 and the signal  from microphone 2 will contain the fundamentals and corresponding harmonics of both instruments, but they will differ in their spectral amplitudes. Consider a particular frame for these 2 signals, which corresponds to the exact same music part (i.e., some time alignment procedure will be necessary to align the two microphone signals). Each of the two audio frames is modeled by the source/filter model:
from microphone 2 will contain the fundamentals and corresponding harmonics of both instruments, but they will differ in their spectral amplitudes. Consider a particular frame for these 2 signals, which corresponds to the exact same music part (i.e., some time alignment procedure will be necessary to align the two microphone signals). Each of the two audio frames is modeled by the source/filter model:

From the previous discussion it follows that the two residual signals  and
and  will contain the same harmonic frequency components. If the envelope modeling was perfect, then it follows that they would also be equal (differences in total gain are of no interest for this application), since they would have flat magnitude with exactly the same frequency components. In that case, it would be possible to resynthesize each of the two audio frames using only the AR filter that corresponds to that audio frame and the residual signal of the other microphone. The final signal is resynthesized from the audio frames using the overlap-add procedure. If, similarly, the source/filter model was used for all the spot microphone signals of a single performance, it would be possible to completely resynthesize these signals using their AR vector sequences (one vector for each audio frame) and the residual error of only one microphone signal. This would result in a great reduction of the datarate of the multiple microphone signals.
will contain the same harmonic frequency components. If the envelope modeling was perfect, then it follows that they would also be equal (differences in total gain are of no interest for this application), since they would have flat magnitude with exactly the same frequency components. In that case, it would be possible to resynthesize each of the two audio frames using only the AR filter that corresponds to that audio frame and the residual signal of the other microphone. The final signal is resynthesized from the audio frames using the overlap-add procedure. If, similarly, the source/filter model was used for all the spot microphone signals of a single performance, it would be possible to completely resynthesize these signals using their AR vector sequences (one vector for each audio frame) and the residual error of only one microphone signal. This would result in a great reduction of the datarate of the multiple microphone signals.
3.1. Multiresolution Analysis
The AR model is very useful in speech synthesis and transformations but not as efficient for audio signals. In this section, we are interested to derive an AR-based model which can be successfully applied to audio signals based on multiresolution analysis. It is of interest to investigate the reasons why the AR model is not sufficient for audio as opposed to speech signals. The explanation is based on the nature of audio signals which differ from speech signals in two ways: (a) audio signals cover the frequency range 0–20 kHz, while speech signals are mostly concentrated below 10 kHz and (b) audio signals are richer in their frequency content than speech signals since typically they contain a collection of harmonic signals (i.e., instruments and singing), while speech typically refers to only one harmonic source (one voice only). At the same time, for the application examined in this paper, it must be taken into consideration that the AR filter is not an exact representation of the spectral envelope of the audio frame, and the residual signals for the two microphone signals will not be equal. All these issues are addressed in our manuscript by the use of the multiresolution AR model. The spectrum of the audio signals is divided into frequency bands, and LP analysis is applied in each band separately (subband signals are downsampled). A small AR filter order for each band can result in much better estimation of the spectral envelope than a high-order filter for the full frequency band. The multiband source/filter model achieves a flatter frequency response for the residual signals. Then one of them can be used for resynthesizing the other microphone signals, in the manner explained in the previous paragraph. In fact, it has been theoretically shown that the prediction error (residual) signal obtained using linear prediction in subbands is flatter in the frequency domain than the prediction error obtained using fullband linear prediction (for the same AR filter order) [22]. This is equivalent to the fact that subband LP is superior to fullband LP. In the example of Figure 1, the power spectral density (PSD) of a particular audio frame is shown, in the frequency region 0–700 Hz (the plot is limited within this range for improved frequency resolution). The audio frame used in this figure is extracted from the audio signals used later in our simulations. The solid line corresponds to the original PSD of the audio signal, while the dashed line corresponds to the AR spectrum using subband analysis (10th order AR filter, 4 subbands used). The dashed-dotted line corresponds to the fullband AR spectrum for the same filter order. It is clear from the figure that subband LP is far superior to the fullband LP, which translates into a flatter frequency spectrum for the prediction error signal of the subband LP. The combined AR subband PSD can be obtained from the subband analysis by upsampling and filtering the subband correlations, as explained in [22]. It is of interest to note that for equal LP order, the fullband and subband LP result in exactly the same number of LP vectors for a particular recording; this is due to the multiresolution analysis and to the critical subsampling for each band (combined with different frame rate for each subband). Thus in terms of bitrate, same prediction order for the fullband and the subband LP can be considered equivalent. This is more clearly explained in Section 5, when specific examples for the number of bands and frame rate per band are discussed.
3.2. Crosstalk Issue
In practice, the prediction error signals cannot be made exactly flat (and thus equal), thus the resynthesized signals will not sound exactly the same as the originally recorded signals. Additionally, if the reference signal is the sum of the various spot signals (which is necessary when the various microphone signals do not contain common information), frequency components will appear in the downmix that should not be included in the residual of all spot signals. These issues will result in the introduction of crosstalk in the spot recordings that was discussed in Section 2. We claim that the use of the multiband source/filter model results in audio signals of good quality which retain the "objective" of the initial recordings (i.e., the main music part of the recording remains prominent), with only a small amount of crosstalk. In other words, the "main" instrument that is captured still remains the prominent part of the microphone signal, while other parts of the orchestra might be more audible in the resynthesized signal than in the original microphone signal (crosstalk). Returning to the example of the two microphones and the two instruments, if the residual of microphone 1 is used in order to resynthesize the signal of microphone 2, then in the result the violin will most likely be more audible than in the original microphone 2 signal. This happens because some information of the first microphone signal remains in the error signal, since the spectral envelope modeling is not perfect. However, the trumpet will still be the prominent of the two instruments in the resynthesized signal for microphone 2, since we used the original spectral information of that microphone signal. It is also of interest to note the fact that the amount of crosstalk and the final audio quality of the multiband source/filter model depends on the following parameters: (1) the duration of the audio frames for each band, (2) the AR order for each band, (3) the percentage of frame overlapping, (4) the total number of bands, and (5) the filterbank used. By changing these parameters we can achieve various datarates with the corresponding varying audio quality. However, a particular choice for all these parameters can be found experimentally to achieve the best possible modeling performance (example values are given in Section 5 for the particular waveforms we used for testing the method).
3.3. Model Overview
Based on the analysis of the previous paragraphs, at this point a brief overview is given of the overall encoding/decoding scheme. At the coding side, we are interested to encode the various microphone signals (Recordings 1-N in Figure 2), of a given multimicrophone recording. For example, in this paper (Section 5), parts of a 16 microphone recording of a particular concert hall performance are used. Each of the 16 microphone signals is to be processed independently under the proposed scheme. One of the microphone signals is chosen to be the reference recording (Recording 1 in Figure 2). This signal is encoded as a single audio channel, that is,using a perceptual audio coder. The remaining 15 microphone signals are processed using an analysis filterbank, followed by linear prediction in each of the subbands. Only the AR parameters for each band are encoded (corresponding to the spectral envelopes of the short-time spectra), while the residual signals are discarded. At the decoder, the inverse procedure is followed. The reference signal is obtained using the decoder of the perceptual audio coder. From the reference signal, the residual is extracted, which is to be used to resynthesize the subband signals of the 15 remaining microphone signals along with the corresponding AR decoded parameters. This procedure is followed by the synthesis filterbank, which produces the final resynthesized microphone signals of the multimicrophone recording.
Diagram of the proposed encoding approach. Each of the microphone signals of the multimicrophone recording is processed by an analysis filterbank. Each of the subband signals is modeled using the source/filter model, and for each microphone signal, only the AR parameters are encoded. Recording 1 corresponds to the reference signal, which is encoded as a single audio channel; the residual of the reference signal will be used to resynthesize the remaining microphone signals at the receiving end.
As mentioned in Section 1, given that the remaining microphone signals require minimal rates for encoding (in the order of 5 kbps), our approach is to encode the various microphone signals before those are mixed; thus mixing can take place at the receiving end. We note that the residual of the reference signal will be used to resynthesize all the remaining microphone signals, so the reference signal must be carefully chosen. For the example of concert hall performances, empirically, it is best if this signal corresponds to a microphone location that is in some distance from the orchestra so that it contains the instruments with equal weight. At the same time, it is important that this microphone is not placed in a large distance from the orchestra, so that it does not capture a large degree of the hall reverberation. In that case, the resynthesized signals will sound more reverberant than the original recordings, since the short-time spectral whitening we perform cannot capture a long-term effect such as reverberation. The choice of the reference signal is an open question, and it is a problem that depends on the properties of the particular recording to be encoded. We remind the reader the fact that the reference signal can be a sum of all microphone signals, and the practical implications of this latter approach are examined in Section 5.
In Section 5, it is verified experimentally that our claims hold for other cases of harmonic signals, such as speech signals. It should be noted that some specific types of microphone signals, such as percussive instruments and signals from microphones far from the source, present different challenges that were considered in our previous work [19]. The method proposed in this paper focuses on the large class of audio signals that can be modeled using a short-time analysis approach with emphasis on their spectral envelope (as opposed to the residual signal).
4. Spot Signals Coding
The next step in the proposed algorithm is to quantize the spectral envelopes for each of the microphone signals. This is done separately for each of the frequency bands in which we divide the microphone signals. The quantization scheme of [18] is followed here, which was developed for vector quantization of speech line spectral frequencies (LSFs). The AR coefficients of each microphone signal are transformed to LSFs, since LSFs are more resistant to quantization errors. Next, the LSF sequence that is obtained from each microphone signal is modeled with the use of a Gaussian mixture model (GMM)

where  is the normal multivariate distribution with mean vector
is the normal multivariate distribution with mean vector  and covariance matrix
and covariance matrix  ,
,  is the number of clusters, and
is the number of clusters, and  is the prior probability that the observation
is the prior probability that the observation  has been generated by cluster
has been generated by cluster  . The LSF vector order is denoted as
. The LSF vector order is denoted as  (i.e.,
(i.e.,  th order linear prediction). GMMs are suitable for this problem since they have been shown to model successfully the statistics of spectral vectors of both speech [18, 23] and audio signals [19]. The Karhunen Loeve transform (KLT) is adopted for the LSFs decorrelation. KLT is especially fit for GMM-modeled parameters since it is the optimal transform for Gaussian signals in a minimum-distortion sense. Using GMMs, each LSF vector is assigned to one of the Gaussian classes using some classification measure, thus is considered as approximately Gaussian and can be best decorrelated using the KLT.
th order linear prediction). GMMs are suitable for this problem since they have been shown to model successfully the statistics of spectral vectors of both speech [18, 23] and audio signals [19]. The Karhunen Loeve transform (KLT) is adopted for the LSFs decorrelation. KLT is especially fit for GMM-modeled parameters since it is the optimal transform for Gaussian signals in a minimum-distortion sense. Using GMMs, each LSF vector is assigned to one of the Gaussian classes using some classification measure, thus is considered as approximately Gaussian and can be best decorrelated using the KLT.
Using the GMM modeling of the spectral parameters, it holds for the covariance matrix of each class that it can be diagonalized using the eigenvalue decomposition as

where  and
and  . In other words,
. In other words,  is the diagonal matrix containing the eigenvalues, and
is the diagonal matrix containing the eigenvalues, and  is the matrix containing the corresponding set of orthogonal eigenvectors of
is the matrix containing the corresponding set of orthogonal eigenvectors of  , for the
, for the  th Gaussian class of the model. Then KLT substitutes each spectral vector for time segment
th Gaussian class of the model. Then KLT substitutes each spectral vector for time segment  ,
,  , with another vector of decorrelated components
, with another vector of decorrelated components 

Similarly, the inverse KLT procedure (IKLT) reconstructs  from
from  using the inverse relation
using the inverse relation

A nonuniform quantizer is achieved by a combination of a compressor, a uniform quantizer, and an expander. The decorrelated vectors are processed using a logarithmic compression function, quantized by a uniform quantizer, and expanded using the inverse of the compression function. The companding method of [24] was used, since this function resulted in robust quantization in our experiments. A bit allocation scheme for the uniform quantizer is needed in order to allocate the total available bits (denoted by  and specified by the user) for quantizing the source, among the various clusters of the GMM. Let
and specified by the user) for quantizing the source, among the various clusters of the GMM. Let  be the bits for quantizing cluster
be the bits for quantizing cluster  , and
, and  the quantity
the quantity

where  is the dimensionality of the LSF vector.
is the dimensionality of the LSF vector.
4.1. Fixed Rate Coding
In the fixed rate bit allocation scheme, the length of the codewords is fixed and can be easily found to satisfy the constraint  . Subject to this constraint, the optimal bit allocation which minimizes the total average mean square distortion is given by [18]
. Subject to this constraint, the optimal bit allocation which minimizes the total average mean square distortion is given by [18]

4.2. Variable Rate Coding
In the variable rate bit allocation scheme, some of the total bits (denoted  ) are used for the cluster identification. Thus the variable rate constraint becomes
) are used for the cluster identification. Thus the variable rate constraint becomes  where
where  . In a variable rate quantizer, the average rate of the quantizer is fixed, which translates into the constraint
. In a variable rate quantizer, the average rate of the quantizer is fixed, which translates into the constraint  . Subject to the above constraints, the optimal bit allocation which minimizes the total average mean square distortion is given by [18]
. Subject to the above constraints, the optimal bit allocation which minimizes the total average mean square distortion is given by [18]

After the evaluation of the cluster allocated bits, the bit allocation among the cluster dimensions is given by

where  is the allocated bits to the
is the allocated bits to the  th component of the
th component of the  th cluster and
th cluster and  is the
is the  th eigenvalue of cluster
th eigenvalue of cluster  . In our implementation we rounded
. In our implementation we rounded  in the nearest integer number for more accurate bit allocation.
in the nearest integer number for more accurate bit allocation.
To summarize, the procedure for coding the LSF vectors of each frequency band is as follows.
4.2.1. Cluster Quantization
The quantization of an LSF vector with the parameters of  th cluster (Figure 3) consists of the following stages:
th cluster (Figure 3) consists of the following stages:
-
(i)
the LSF vector
 is mean-subtracted, using the mean
is mean-subtracted, using the mean 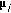 of the cluster
of the cluster  ;
;
(ii)the resultant vector is decorrelated using the matrix  ;
;
-
(iii)
the vector's components are passed through a nonuniform quantizer (compressor, uniform quantizer, expander);
-
(iv)
the correlated version of the quantized vector is reconstructed using the matrix
 ; and
; and -
(v)
finally, the cluster mean
 is added to obtain the quantized value of
is added to obtain the quantized value of  by the
by the  th cluster,
th cluster, 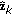 .
.
Overall quantization scheme, for each frequency band. Each LSF vector is mean normalized and decorrelated, using parameters of the GMM class that the vector was classified to. Decorrelation is followed by nonuniform quantization of the vector components, and this procedure is inverted to obtain the quantized LSF vector.
4.2.2. Overall Quantization
A specific LSF vector  is quantized with the use of every cluster of the GMM as described. In order to choose the GMM cluster that best models a particular LSF vector, the relative distortion value is computed for the vector, and the one with the minimum distortion is chosen (Figure 4). Here the log spectral distortion (LSD) is employed as a measure of distance as in [18]
is quantized with the use of every cluster of the GMM as described. In order to choose the GMM cluster that best models a particular LSF vector, the relative distortion value is computed for the vector, and the one with the minimum distortion is chosen (Figure 4). Here the log spectral distortion (LSD) is employed as a measure of distance as in [18]

where  is the sampling rate,
is the sampling rate,  ,
,  are, respectively, the LPC power spectra corresponding to the original vector
are, respectively, the LPC power spectra corresponding to the original vector  and the quantized vector
and the quantized vector  , for each cluster
, for each cluster  . The bitwise representation of
. The bitwise representation of  , corresponding to the cluster of minimum LSD, is transmitted. At the receiver, the quantized LSF vector is converted into its corresponding LPC value which is used to resynthesize the audio signal of the
, corresponding to the cluster of minimum LSD, is transmitted. At the receiver, the quantized LSF vector is converted into its corresponding LPC value which is used to resynthesize the audio signal of the  th frame.
th frame.
5. Results
For our experiments, we use microphone signals obtained from a US orchestra hall by placing 16 microphones at various locations throughout the hall. (Provided by Professor Kyriakakis of the University of Southern California.) Our objective is to indicate that the model and the coding method we propose result in a good-quality recording with low datarate requirements. For this purpose, we use two of these microphone signals, where one of the microphones mainly captures the male voices of the chorus of the orchestra, while the other one mainly captures the female voices. These recordings are very easy to distinguish acoustically. In Section 5.2, some additional sound signals are used for examining the scenario when the reference signal might be a sum of the various spot recordings. The efficiency of the proposed algorithm is tested via objective and subjective tests.
5.1. Modeling Performance
In this section, we show that the use of the proposed method results in a modeled signal that is objectively and subjectively very close to the original recording. For this purpose, we use the two microphone recordings of the male and female voices of the chorus, as mentioned. The objective is to resynthesize one of these recordings using its corresponding low-dimensional model coefficients along with the residual of the other recording.
From initial listening tests, it has been clear that using a number of bands around 8 for our model produced high-quality resynthesis without loss of the objective of the initial recording. For example, we have been able to resynthesize the male voices recording based on the residual from the female voices. On the other hand, without the use of a filterbank, the resulting quality of the resynthesized signal greatly deteriorated with an introduction of a large degree of crosstalk to the recording. In order to show this objectively, we measured the distance between the residual signals of the two recordings, using the normalized mutual information as a distance measure. The intuitive claim, as explained in Section 3, is that decreasing the distance of the two residuals will increase the quality of the resynthesized recording. Our listening tests indicated that increasing the number of subbands in our model, and consequently improving the model accuracy, resulted in much better quality of the resynthesized signals. While several measures were tested, the normalized mutual information proved to be very consistent in this sense.
The use of mutual information  as a distance measure between random variables
as a distance measure between random variables  and
and  is very common in pattern comparison. By definition, the mutual information of two random variables
is very common in pattern comparison. By definition, the mutual information of two random variables  and
and  with joint probability density function (pdf)
with joint probability density function (pdf)  and marginal pdfs
and marginal pdfs  and
and  is the relative entropy between the joint distribution and the product distribution, that is,
is the relative entropy between the joint distribution and the product distribution, that is,

It is easy to prove that

where  is the entropy of
is the entropy of  and
and  is the conditional entropy. The mutual information is always positive. Since our interest is in comparing two vectors
is the conditional entropy. The mutual information is always positive. Since our interest is in comparing two vectors  and
and  (
( being the desired response), it is useful to use a modified definition for the mutual information, the normalized mutual information (NMI)
being the desired response), it is useful to use a modified definition for the mutual information, the normalized mutual information (NMI)  which can be defined as (see also [25, page 47])
which can be defined as (see also [25, page 47])

for which it can be shown that  . The NMI obtains its minimum value when
. The NMI obtains its minimum value when  and
and  are statistically independent and its maximum value when
are statistically independent and its maximum value when  . The NMI does not constitute a metric since it lacks symmetry, however it is invariant to amplitude differences [26], which is very important when comparing audio waveforms.
. The NMI does not constitute a metric since it lacks symmetry, however it is invariant to amplitude differences [26], which is very important when comparing audio waveforms.
In Figure 5 we plot the NMI between the power spectra of the two residual signals with reference to the number of different subbands used, for different orders of the Daubechies wavelet filters, which were used for our tree-structured filterbank [27]. As a result, our filterbank has the perfect reconstruction property, which is essential for an analysis/synthesis system, and also octave frequency-band division. For our implementation, the parameters that produced the best perceptual quality (32nd order LP filter for a 1024 sample frame, corresponding to about 23 milliseconds for 44.1 kHz sampling rate) were used for the full-band analysis. For the subband analysis, we used an 8th order filter for each band, with a constant frame rate of 256 samples for each band (thus varying frame in millisecond, given that the wavelet filterbank is followed by critical subsampling). The amount of overlapping for best quality was found to be 75% for all cases. These parameters were chosen for best perceptual quality while keeping the total number of transmitted coefficients for the resynthesized recording the same for both the fullband and the subband cases. (These parameters are used throughout Section 5, while the number of subbands varies in the experiments.) For the particular choice of parameters mentioned, the total number of coefficients used for the resynthesis is eight times less than the total number of audio samples. The coefficients that we intend to code for each microphone signal are the line spectral frequencies (LSFs) given their favorable quantization properties.
The NMI values in Figure 5 are median values of the segmental NMI between the power spectra of the two residual signals using an analysis window of 6 milliseconds. The residual signals are obtained using an overlap-add procedure so that they can be compared using the same analysis window. Our claim, that using a subband analysis with a small LP order for each band will produce much better modeling results than using a high LP order for the full frequency band, is justified by the results shown. For the full band analysis, we obtain an NMI value of 0.0956 while for an 8-band filterbank the median NMI is 0.5720 (40th order wavelet filters). In Figure 5 we plot the median NMI for different orders of the Daubechies filters. We can see that increasing the filter order results in slightly better results. Intuitively this was expected; an increase in the filter order results in better separation of the different bands, which is important since we model each subband signal independently of the others. In a similar experiment, we compared the residual signals in the time domain and found that the median NMI doubles when using the 8-band system when compared to the full-band case. The results for both the frequency and time domains are similar regardless of the analysis window length for obtaining the NMI segmental values. When increasing the window size, the NMI drops, which is expected since more data are compared. The decrease is similar for the various numbers of bands we tested.
In order to test the performance of our method in terms of crosstalk , we also employed subjective (listening) tests, in which a total of 17 listeners participated (individually, using good-quality headphones—Sennheiser HD 650). We used the two concert hall recordings from the same performance as mentioned earlier (one capturing the male voices and one capturing the female voices of the chorus). We chose three parts of the performance (about 10 seconds each, referred to as Signals 1–3 here) where both parts of the chorus are active so that the two different microphone signals can be easily distinguished. For each signal we designed an ABX test, where A and B correspond to the male and female chorus recording (in random order), while each listener was asked to classify X as being closer to A or B regarding as to whether the male or female voices prevail in the recording.
For this test, as well as all the listening tests employed for the results of this manuscript (both ABX and DCR tests explained in the following paragraphs), the sound level of all waveforms was normalized so that they sound as having equal level (or else the loudness level could have affected the results). This normalization was achieved by dividing each signal with its maximum absolute value, and in practice this procedure proved to be sufficient for all signals to sound as having the same sound level; the reader is referred to the authors' website mentioned in Section 5.2 for listening to the audio waveforms that were used in the listening tests. For both the ABX and DCR tests, a simple computer-based graphical user interface (GUI) was designed for the convenience of the listeners. The GUI consisted of a series of three buttons for the ABX test (two buttons for the DCR test), each button triad (or dyad for the DCR test) corresponding to the same part of a music recording. By clicking to a button in the screen using the mouse, the listener could listen to the corresponding audio file. As is common in these tests, the listener was encouraged to listen to audio clips as many times as desired and in any order preferred.
We tested 4 different types of filterbanks (3 wavelet-based and 1 MDCT-based), namely, 8-band with filters db40 (ABX-1 test) and db4 (ABX-2), 2-band with db40 (ABX-3) and 32-level MDCT-based with KBD window (ABX-4). For each of these 4 tests, we used all three of the chosen signals, thus a total of 12 ABX tests was conducted per listener. The results are given in Table 1. We can conclude that the objective results, as well as the various claims made in the previous sections regarding the model, are verified by the listening tests. It is clear that the 8-level wavelet-based filterbank (ABX-1) produces good results when aliasing is limited (i.e., db40 case), although there is certainly room for improvement and further enhancements to our model are currently examined. On the other hand, when aliasing is high (ABX-2) or when the number of bands (and thus the modeling accuracy) drops (ABX-3), the performance of the proposed method greatly deteriorates, not only in the sense of enhancing the male voices, but also regarding the final quality (which most listeners noticed during the experiments). Crosstalk is increased (but quality remains good) in the case of the MDCT-based filterbank as well (ABX-4). In other words, we noticed that octave filterbanks produce results far superior when compared to equally spaced filterbanks, which could be attributed to the fact that the LP algorithm is especially error-prone in lower-frequency bands. At this point we note that in our informal tests the Laplacian pyramid, which is a different type of octave-spaced filterbank [28], produced results comparable to the wavelet case. This filterbank was used only for verifying the importance of octave-spacing in the filterbank and it is not a viable alternative to wavelets for our method since it is not critically subsampled. The choice of filterbank and whether octave-spaced filterbanks are indeed better from equal-spaced for our model is a subject of our ongoing research.
We also conducted degradation category rating-based (DCR) listening tests for evaluating the quality of the resynthesized signals using a 5-grade scale in reference to the original recording (5 corresponding to being of same quality, and 1 to the lowest quality, when compared with the original male chorus recording). This test is often performed for speech coding [29]. The 17 subjects (the same who participated at the ABX test), listened to the three sound clips (Signals 1–3), where the resynthesized signals were obtained using the best modeling parameters (8-level db40 wavelet-based). The results are depicted in Figure 6, where graphical representations of the 95% confidence interval are shown (the x's mark the mean value and the vertical solid lines indicate the confidence limits). These results show clearly that the resynthesized signals are of good quality and the model does not seem to introduce any serious artifacts.
Results from the 5-grade scale DCR-based listening tests that give a performance indication regarding the resulting quality of the proposed model. Graphical representations of the 95% confidence interval are shown (the x's mark the mean value and the vertical solid lines indicate the confidence limits).
5.2. Donwmix Subjective Tests
In this section, the focus is on testing whether resynthesis of the various spot signals from a downmix sum signal is a viable scenario. This is important in cases when spot signals do not contain common content, which is often the case in studio recordings. As in the previous section, we are again interested to test the amount of crosstalk that is introduced, and whether there are implications regarding the quality of the resynthesized signals. It is expected that it will be more difficult to resynthesize good-quality spot signals from the sum signal compared to the reference signal that was used in the previous section since the sum signal will contain frequency components which were not at all present in some spot signals. Also, crosstalk will be more audible in separate track recordings.
The following recordings were used, each containing a separate instrument recording:
-
(i)
bass singer,
(ii)soprano,
-
(iii)
trumpet,
(iv)harpsichord,
(v)violin,
(vi)rock singer,
(vii)rock guitar,
(viii)male speech, and
(ix)female speech.
Signals (i)–(v) are excerpts from the EBU SQAM (Sound Quality Assessment Material) test disc and were obtained from (http://sound.media.mit.edu/mpeg4/audio/sqam/). These are stereo recordings, and only one of the 2 channels was used in our experiments. Signals (vi)-(vii) are a courtesy of rock band "Orange Moon." Signals (viii)-(ix) were obtained from the VOICES corpus (http://www.cslu.ogi.edu/corpora/voices/), available by OGIs CSLU [30]. All signals are 16-bit 44.1 kHz signals, except from the speech signals which are 22 kHz signals. The modeling parameters used for the experiments of this section correspond to the parameters of ABX-1 test of the previous section, which gave the best objective and subjective results, with the exception of LP order per band which was 16 (instead of 8). In the speech files, though, due to the use of different sampling rate, only 4 subbands were used (instead of 8).
The listening tests employed are ABX and DCR tests. 14 volunteers participated in these tests, and sound was presented using good-quality headphones. Each sound file used was a sum of two original recordings, and more specifically the following signals were created:
-
(1)
bass plus soprano,
(2)guitar plus rock singer,
(3)harpsichord plus violin,
(4)female plus male speech,
(5)trumpet plus violin,
(6)violin plus guitar, and
(7)violin plus harpsichord.
These seven signals correspond one-to-one to the Tests (1)–(7) in the ABX resuls, and to Signals (1)–(7) in the DCR results.
The instrument that is referred first in the above list is the instrument that we wanted to resynthesize from the sum signal. In the ABX test, each listener was presented with the original two instrument recordings that were used to obtain the sum signal as signals A and B (in random order), as well as the resynthesized signal (Signal X), and was asked to associate X with A or B depending on which instrument prevails in the recording. In the DCR tests, each listener was asked to grade the resynthesized signal compared to the original recording that we wanted to obtain (regardless to whether the listener recognized that this was indeed successful in the ABX test). The audio files that were used in these tests can be found in (http://www.ics.forth.gr/~mouchtar/originals/tests.html), which includes the classical music recording of the previous section. These sound files include the separate recordings as well as the sum signal.
The results of the ABX test are given in Table 2. The ABX results clearly show that the amount of crosstalk is small, when considering which instrument prevails in the resynthesized recording, which is a very encouraging result. The total ABX score for all files is 97%. Figure 7 shows the DCR results for the seven test signals. Each listener was asked to grade the resynthesized signal with respect to the original signal we want to model. From the results of the figure we can make the following conclusions.
(i)While singing voices were graded best among the various test signals, speech received one of the lowest grades.
-
(ii)
As expected, when attempting to resynthesize the violin using a sum with the harpsichord, the DCR result is very low. On the other hand, when attempting to obtain the harpsichord from the same sum signal, the DCR result is much better. This is due to the fact that percussive sounds cannot be adequately modeled by their spectral envelope, and significant information remains in the residual. Thus it is a difficult task to diminish the percussive signal when resynthesizing another spot signal, but the opposite is not as hard.
-
(iii)
The same conclusion holds for the vocals and the guitar signals, but to a lesser degree, given that in our tests the guitar has a percussive nature but not to the same degree as the harpsichord.
Given the SQAM waveforms, we also derived some test audio files for illustrating some interesting aspects of the proposed modeling approach. One subject of interest is to show that the residual signal of the reference channel is needed for good-quality synthesis, as opposed to using a synthetic error signal such as white noise or a randomly chosen segment from the actual error signal of the target signal. As is true for speech signals as well, white noise cannot be used as an error signal for synthesizing high-quality audio signals. In fact, in speech processing the problem of producing the best model error signal for achieving best audio quality has been an important issue both in text-to-speech synthesis (TTS) and speech coding alike. This problem is even more important in music applications as the one examined in the text, where quality is of extreme importance. It is thus necessary to note the fact that using white noise as model error, even with the correct energy scaling for each time frame, will not produce high-quality synthesis in our application, nor in speech synthesis and coding. The same is true for more carefully designed synthetic error signals (e.g., for speech an impulse train can be generated based on the estimated pitch, although this in practice is not possible for polyphonic music). The reason is that the whitening process is not perfect and important information remains in the error signal. This information cannot be approximated by white noise or any other synthetic signal but can be approximated by a similar error signal (obtained from the reference signal). The general practice in the speech processing domain is to use the error from actually recorded speech signals (e.g., phonemes, as in concatenative speech synthesis). Similarly in our case, the error signal is not synthesized but it is obtained from actually recorded signals (the reference recording), and this is possible only for the case that we examine here, that is, for various spot signals of a multichannel recording, which have similar content. If the various spot signals were not correlated, the proposed method would fail (unless a downmix signal was derived as a reference signal), since the model error signals must be very similar in order to use one error signal for synthesizing all spot signals.
The other issue that we wish to illustrate at this point using the SQAM waveforms is that the creation of a downmix signal is necessary for the case when the reference and target signals become uncorrelated. For simplification, let us consider one reference and one spot signal. The proposed method assumes that the two microphone signals have similar content, in the sense that the microphones capture the same instruments with different weights (e.g., one microphone captures mostly the male voices of the chorus but the female voices are also present in the recording, and vice versa for the other microphone). In principle, the whitening process of removing the AR spectrum (improved by multiresolution analysis) will result in two error signals with the same content. This, as explained in the manuscript, is due to the fact that the two error signals will contain the same frequencies (harmonics) with equal amplitude (due to whitening). This concept is central in the proposed method. When the reference and target signals are not correlated, or are weakly correlated, the proposed method will result in poor quality (the two error signals will contain different harmonics even in the ideal case of perfect whitening).
In order to show examples of the resulting audio quality that is obtained in the above described cases, we have derived the audio waveforms that can be found in our previously mentioned website, in subdirectory named "Incorrect Error Synthesis Examples." In these test audio files, we have included an experiment where we use the violin and trumpet recordings from the SQAM dataset. Our objective is to resynthesize the trumpet signal using only its multiband AR spectrum and (i) white noise scaled using the correctly extracted variance (i.e., obtained from the corresponding subband and time frame of the trumpet error signal), (ii) from a randomly selected frame of the trumpet signal (different one for each subband), again scaled with the "correct" variance of each frame, and (iii) using the error signal from the violin recording. The above experiments were derived so that we can verify our claims regarding the fact (a) that random noise or an irrelevant error signal cannot produce high-audio quality (experiments (i) and (ii)) and (b) that the downmix process is necessary for introducing correlation between the reference and target signals. The listener can easily verify these claims by comparing the resynthesis result from the downmix signal which can be found in the aforementioned link ("Trumpet-violin" subdirectory).
As a general conclusion, resynthesis from a sum signal is a more challenging task than from a signal which originally contains common information with all spot signals (as is the case in USCs classical music recordings). However, as we also note later in Section 5.3, the DCR results obtained do not necessarily indicate the quality of the resynthesized signals alone. The fact that in the resynthesized signals there is an amount of crosstalk which is not present in the original recording affects the DCR tests, although the actual audio quality of the signal might not be distorted. This can be seen if we compare the results of this section with the results of Section 5.1. As opposed to Section 5.1, in this section, the actual separate recordings were available and were used for testing. Consequently, the ABX results obtained for the sum scenario were much better since it is easier to identify the target recording than in Section 5.1. On the other hand, since now the original recordings contain separate instruments, in the DCR test the effect of crosstalk is much more evident and is considered more important by the listeners than in Section 5.1. In other words, the DCR results in this section are more related with the crosstalk issue rather than the resulting quality. We invite the reader to judge on the performance of the proposed model by visiting our aforementioned website.
5.3. Coding Results
Regarding the coding scheme proposed, our initial listening tests indicated that the final quantized version is acoustically close in quality compared to the recorded signal, for bitrates as low as 5 kbps. Again, it is mentioned that the objective in this paper is to obtain subjective results above 3.0 grade, which can be considered a good performance for low bitrate coding applications. First, we give some objective results using the LSD measure. The audio data used for the LSD results correspond to about 1 minute of the male and female chorus classical music recordings that have been used in Section 5.1. Classical music signals 1–3 that were used in the listening tests of Section 5.1 (and are used for the listening tests of this section as well) are part of this 1 minute testing dataset. The sampling rate for the audio data is 44.1 kHz; we divide the frequency range into 8 octave subbands using  th order Daubechies wavelet filters. The model parameters are those that gave the best quality in the modeling (objective and subjective) results of the previous section, that is, 8th order LP, 256 samples frame with 75% overlapping.
th order Daubechies wavelet filters. The model parameters are those that gave the best quality in the modeling (objective and subjective) results of the previous section, that is, 8th order LP, 256 samples frame with 75% overlapping.
Before proceeding to the description of the results, we give some details regarding the GMM training procedure. A training audio dataset of about 136 000 LSF vectors (approximately 3 minutes of audio) was used to estimate the parameters of a 16-class GMM. The training database consists of recordings of the same performance as the data we encode (but a different part of the recording than the one used for testing). In practice, it may not be possible to obtain a training set that corresponds to the same data that are coded. In these cases, it is possible to use a training database which contains a large number of music recordings, which translates into a large degree of variability in the LSF parameters. It is also possible to use only a subset of the large database which is closer in content to the content that will be coded.
For obtaining this LSF vector training dataset, we applied to the audio data the same wavelet-based filterbank that is used for the modeling/encoding procedure (8-bands, critical subsampling, same window length in samples for each band). In this manner, we collected all the subband vectors into one set of 136 000 LSF vectors; with this set we trained a single GMM that was used for decorrelating all subband vectors during the coding procedure. While this approach was followed in this paper, it is important to note that a problem arises regarding the lack of training vectors in the lower subbands. More specifically, under these model parameters, the number of vectors in the  th band is double the number of vectors in the
th band is double the number of vectors in the  th and so forth. Consequently, the training dataset contains more vectors from—and is thus more accurate for—the higher-frequency bands than the lower-frequency bands. In turn, during coding, the lower bands demand more bits/frame for achieving the same LSD with the higher-frequency bands. On the other hand, this does not significantly increase the total bitrate since the critical subsampling results in far less data in the lower bands. Nevertheless, we attempted to resolve this issue by using the same frame rate in millisecond (varying in samples) for each band during training, which results in the same number of training vectors per band. We trained a model using the vectors from all bands as one training set. We also trained a different model, by creating 8 training sets (different GMM for each band), given that in this case there are enough vectors in all subbands for training a different GMM per band. Both of these latter approaches produced much higher LSD than our initial approach, mostly in the lower-frequency bands. This can be possibly attributed to the fact that the training and testing conditions are different (in our case the analysis/synthesis frame rate for each band). In turn, this results in a mismatch between the training and testing vectors, which is evident in terms of LSD.
th and so forth. Consequently, the training dataset contains more vectors from—and is thus more accurate for—the higher-frequency bands than the lower-frequency bands. In turn, during coding, the lower bands demand more bits/frame for achieving the same LSD with the higher-frequency bands. On the other hand, this does not significantly increase the total bitrate since the critical subsampling results in far less data in the lower bands. Nevertheless, we attempted to resolve this issue by using the same frame rate in millisecond (varying in samples) for each band during training, which results in the same number of training vectors per band. We trained a model using the vectors from all bands as one training set. We also trained a different model, by creating 8 training sets (different GMM for each band), given that in this case there are enough vectors in all subbands for training a different GMM per band. Both of these latter approaches produced much higher LSD than our initial approach, mostly in the lower-frequency bands. This can be possibly attributed to the fact that the training and testing conditions are different (in our case the analysis/synthesis frame rate for each band). In turn, this results in a mismatch between the training and testing vectors, which is evident in terms of LSD.
Using the aforementioned parameter values, and with varying choice of bitrate, we obtain the values of Table 3 (variable rate coding). Fixed rate results are not given here due to space limitations, and since it is well known that variable rate coding is more efficient than fixed rate in terms of LSD. In these tables, the LSD value given is the average LSD over all bands. The percentage of the LSD values that are within the 2–4 dB interval and for those that are greater than 4 dB is also given. These values correspond to the total number of quantized vectors and are not averages of the subband percentages (i.e., all subband vectors are considered as one set for deriving the percentage values). In Table 3, the bits/frame used are the same for all subbands except in the first two cases (for 5 and 10 kbps). For the 5 and 10 kbps cases, a different number of bits/frame is used for each band (for the 5 kbps case the number of bits/frame is given in Table 4). In these latter cases, the number of allocated bits per band is skewed towards the lower-frequency bands, which is a more efficient approach given the lack of training data for the lower bands as mentioned. This explains the fact that in Table 3, the LSD for the 10 kbps is lower than the 15 kbps respective results, which might seem contradictory at first.
We should note that the LSD values given in all the tables of this section offer an objective performance measure which is not trivial to correlate with the acoustic tests that follow later in this section. This is in contrast to speech coding, where it is generally accepted that an average LSD value of 1 dB (combined with less than 2% of LSD values in the region 2–4 dB) will result in speech of high perceptual quality. In our case, there are two issues that prohibit at this point such a generalization. These are (i) the fact that LSF coding for audio signals has not been used in the past for good-quality audio coding, and consequently extensive tests are required and (ii) the use of filterbanks, which raises the issue that for the same average (over all subbands) LSD value, we can achieve a wide range of LSD values per band. The latter remains an open question for our future research, that is, to determine how the LSD per band measure that we use correlates with subjective quality. From our tests, it has been clear that the listeners have different tolerance in the coding error for each subband, which is related to psychoacoustic principles. In our future research, we intend to examine whether a minimum LSD value per band can be derived, similarly to the aforementioned principles in speech coding research.
In order to test the performance of the coding procedure, we conducted DCR-based listening tests, using the aforementioned (in Section 5.1) 5-grade scaling procedure. Twenty-two volunteers listened to three sound clips (originally recorded versus coded classical music Signals 1–3 similarly to Section 5.1). In this case, the coded signals were obtained using the best modeling parameters (8-level db40 wavelet-based), while coded using the variable rate coding scheme with 16 GMM classes. Regarding the bits/frame used for each band, we encoded the audio signals using the following bitrates: (i) 5 kbps with varying bits/frame for each band, (ii) 10 kbps with varying bits/frame for each band, (iii) 15 kbps using 22 bits/frame for each band, and (iv) 20 kbps with 29 bits/frame for each band. The choice of these four bitrate values, for each of the three sound clips mentioned, resulted in a total of 12 DCR tests. The signals 1–3 that were used in the listening tests are part of the 1-minute audio signals that were used to derive the LSD values in this paper.
The results of the DCR tests are depicted in Figure 8, where the 95% confidence interval are shown (the vertical lines indicate the confidence limits). In general, we can deduce from the results of the figure that the quality of the coded audio signals is good and the overall proposed algorithm offers very encouraging performance. Regarding the individual results for each of the 4 different bitrates used for coding, we can see that the 10 and 20 kbps rates result in good-quality coding for all three signals. The 5 kbps rate can be verified to be the minimum rate that can be used so that the coded signals can be considered of acceptable quality (no significant degradation). For Signal-3 especially, the quality of the 5 kbps coded signal is perceived to be lower than the other three coded signals, but still remains acceptable. It is of interest to note that all listeners in our test did not have previous experience in such tests. Thus, although instructed to do otherwise, they seemed to have taken into consideration the fact that the original and coded signals did not sound exactly the same (due to the introduced crosstalk during the modeling procedure). While the crosstalk is important perceptually, it is not related to the quality of the coding procedure, thus the DCR results of both Figures 6 and 8 (as well as of Figure 7 as explained in Section 5.2) indicate a lower signal quality than the one actually achieved. It is also of interest to note that the majority of the listeners found it very hard to distinguish between the various sound clips (corresponding to the various bitrates for coding and the original recordings), which is also an indication that the coding algorithm performed very well even in the very low bitrate cases.
At this point, it is of interest to mention that for the results described in this paper, the residual signal is derived from a PCM coded recording, using 16 bits/sample and a 44.1 kHz sampling rate. In practice, as mentioned, the coding scheme we propose is based on coding a single audio channel (from which the residual is derived) and using side information in the order of 5 kbps for each of the remaining microphone recordings. The single audio channel can be encoded using any monophonic coding scheme, such as perceptual audio coders. In informal listening tests, we used the residual of an MP3 coded signal with 64 kbps rate, for resynthesizing Signals 1–3 using 5 kbps bitrate. The resulting perceptual quality was similar to the quality of the signals used in the listening tests of Figure 8.
6. Conclusions
We proposed a multiresolution source/filter model for immersive audio applications, which can lead to good quality (above 3.0 perceptual grade compared to the original) low bitrate coding. More specifically, we showed that it is possible to encode the multiple microphone signals of a multichannel audio recording into a single audio channel, and additional information in the order of 5 kbps for each microphone signal. The approach followed is focused towards encoding the microphone signals before those are mixed into the final multichannel mix and is thus suitable for immersive applications such as remote mixing and distributed musicians' collaboration. Our objective and subjective results demonstrate that our algorithm offers a viable approach for very low bitrate audio coding, with audio quality that is acceptable for many practical applications.
References
ISO/IEC JTC1/SC29/WG11 (MPEG) International Standard ISO/IEC 11172-3, “Coding of moving pictures and associated audio for digital storage media at up to about 1.5 Mbit/s”, 1992.
Noll P: MPEG digital audio coding. IEEE Signal Processing Magazine 1997,14(5):59-81. 10.1109/79.618009
ISO/IEC JTC1/SC29/WG11 (MPEG) International Standard ISO/IEC 13818-7, “Generic coding of moving pictures and associated audio: advanced audio coding”, 1997.
Bosi M, Brandenburg K, Quackenbush S, et al.: ISO/IEC MPEG-2 advanced audio coding. Proceedings of the 101st Convention of the Audio Engineering Society (AES '96), November 1996, Los Angeles, Calif, USA paper no. 4382
Brandenburg K, Bosi M: ISO/IEC MPEG-2 advanced audio coding: overview and applications. Proceedings of the 103rd Convention of Audio Engineering Society (AES '97), September 1997, New York, NY, USA paper no. 4641
ATSC Document A/52 Digital Audio Compression Standard
Davis M: The AC-3 multichannel coder. Proceedings of the 95th Convention of the Audio Engineering Society (AES '93), October 1993, New York, NY, USA paper no. 3774
Johnston JD, Ferreira AJ: Sum-difference stereo transform coding. Proceedings of IEEE International Conference on Speech, Acoustics and Signal Processing (ICASSP '92), March 1992, San Francisco, Calif, USA 2: 569-572.
Herre J, Brandenburg K, Lederer D: Intensity stereo coding. Proceedings of the 96th Convention of Audio Engineering Society (AES '94), February 1994, Amsterdam, The Netherlands 1-10. paper no. 3799
Painter T, Spanias A: Perceptual coding of digital audio. Proceedings of the IEEE 2000,88(4):451-512. 10.1109/5.842996
Yang D, Ai H, Kyriakakis C, Kuo C-CJ: High-fidelity multichannel audio coding with Karhunen-Loève transform. IEEE Transactions on Speech and Audio Processing 2003,11(4):365-380. 10.1109/TSA.2003.814375
Breebaart J, Herre J, Faller C, et al.: MPEG spatial audio coding /MPEG surround: overview and current status. Proceedings of the 119th Convention of the Audio Engineering Society (AES '05), October 2005, New York, NY, USA paper no. 6599
ITU-R BS.1116 : Methods for the subjective assessment of small impairments in audio systems including multichannel sound systems. 1994.
Baumgarte F, Faller C: Binaural cue coding—part I: psychoacoustic fundamentals and design principles. IEEE Transactions on Speech and Audio Processing 2003,11(6):509-519. 10.1109/TSA.2003.818109
Faller C, Baumgarte F: Binaural cue coding—part II: schemes and applications. IEEE Transactions on Speech and Audio Processing 2003,11(6):520-531. 10.1109/TSA.2003.818108
Breebaart J, van de Par S, Kohlrausch A, Schuijers E: Parametric coding of stereo audio. EURASIP Journal on Applied Signal Processing 2005,2005(9):1305-1322. 10.1155/ASP.2005.1305
Sawchuk A, Chew E, Zimmermann R, Papadopoulos C, Kyriakakis C: From remote media immersion to distributed immersive performance. Proceedings of the ACM SIGMM Workshop on Experiential Telepresence (ETP '03), November 2003, Berkeley, Calif, USA 110-120.
Subramaniam AD, Rao BD: PDF optimized parametric vector quantization of speech line spectral frequencies. IEEE Transactions on Speech and Audio Processing 2003,11(2):130-142. 10.1109/TSA.2003.809192
Mouchtaris A, Narayanan SS, Kyriakakis C: Virtual microphones for multichannel audio resynthesis. EURASIP Journal on Applied Signal Processing 2003,2003(10):968-979. 10.1155/S1110865703304032
Mouchtaris A, Narayanan SS, Kyriakakis C: Multichannel audio synthesis by subband-based spectral conversion and parameter adaptation. IEEE Transactions on Speech and Audio Processing 2005,13(2):263-274.
Haykin S: Adaptive Filter Theory. Prentice-Hall, Englewood-Cliffs, NJ, USA; 1996.
Rao S, Pearlman WA: Analysis of linear prediction, coding, and spectral estimation from subbands. IEEE Transactions on Information Theory 1996,42(4):1160-1178. 10.1109/18.508839
Reynolds DA, Rose RC: Robust text-independent speaker identification using Gaussian mixture speaker models. IEEE Transactions on Speech and Audio Processing 1995,3(1):72-83. 10.1109/89.365379
Bucklew J, Gallagher N Jr.: A note on the computation of optimal mean-squared error quantizers. IEEE Transactions on Communications 1982,30(1, part 1):298-301. 10.1109/TCOM.1982.1095374
Cover TM, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Shekhar C, Chellappa R: Experimental evaluation of two criteria for pattern comparison and alignment. Proceedings of the 14th International Conference on Pattern Recognition (ICPR '98), August 1998, Brisbane, Queensland, Australia 1: 146-153.
Strang G, Nguyen T: Wavelets and Filter Banks. Wellesley-Cambridge, Wellesley, Mass, USA; 1996.
Burt P, Adelson E: The Laplacian pyramid as a compact image code. IEEE Transactions on Communications 1983,31(4):532-540. 10.1109/TCOM.1983.1095851
Kleijn WB, Paliwal KK (Eds): Speech Coding and Synthesis. Elsevier Science, Amsterdam, The Netherlands; 1995.
Kain A: High resolution voice transformation, Ph.D. thesis. OGI School of Science and Engineering, Oregon Health and Science University, Portland, Ore, USA; 2001.
Acknowledgments
The authors wish to thank the listening tests volunteers, Christos Tzagkarakis for helping organize the listening tests, Andre Holzapfel and his rock group "Orange Moon" for providing the rock music test files, and Professor Kyriakakis of the University of Southern California for providing the classical music test files as well as for his overall support of the project. This work has been cofunded by a Marie Curie Transfer of Knowledge (TOK) Grant within the 6th European Community Framework Program and by the European Social Fund and Greek Government National Resources.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mouchtaris, A., Karadimou, K. & Tsakalides, P. Multiresolution Source/Filter Model for Low Bitrate Coding of Spot Microphone Signals. J AUDIO SPEECH MUSIC PROC. 2008, 624321 (2008). https://doi.org/10.1155/2008/624321
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/624321


 is mean-subtracted, using the mean
is mean-subtracted, using the mean 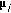 of the cluster
of the cluster  ;
; ; and
; and is added to obtain the quantized value of
is added to obtain the quantized value of  by the
by the  th cluster,
th cluster, 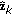 .
.




