- Research Article
- Open access
- Published:
Integrated Phoneme Subspace Method for Speech Feature Extraction
EURASIP Journal on Audio, Speech, and Music Processing volume 2009, Article number: 690451 (2009)
Abstract
Speech feature extraction has been a key focus in robust speech recognition research. In this work, we discuss data-driven linear feature transformations applied to feature vectors in the logarithmic mel-frequency filter bank domain. Transformations are based on principal component analysis (PCA), independent component analysis (ICA), and linear discriminant analysis (LDA). Furthermore, this paper introduces a new feature extraction technique that collects the correlation information among phoneme subspaces and reconstructs feature space for representing phonemic information efficiently. The proposed speech feature vector is generated by projecting an observed vector onto an integrated phoneme subspace (IPS) based on PCA or ICA. The performance of the new feature was evaluated for isolated word speech recognition. The proposed method provided higher recognition accuracy than conventional methods in clean and reverberant environments.
1. Introduction
In the case of distant (hands-free) speech recognition, system performance decreases sharply due to the effects of reverberation. To solve this problem, there have been many studies carried out on feature extraction, model adaptation, and decoding. Our proposed method focuses on the feature extraction domain.
The Mel-Frequency Cepstrum Coefficient (MFCC) is a widely used speech feature. However, since the feature space of a MFCC obtained using Discrete Cosine Transform (DCT) is not directly dependent on speech data, the observed signal with noise does not show good performance without utilizing noise suppression methods. There are other methods for feature extraction: RASTA-PLP [1, 2], normalization [3, 4], Principal Component Analysis (PCA) [5–7], Independent Component Analysis (ICA) [8, 9], and Linear Discriminant Analysis (LDA) [10] based methods.
In [5, 6], the subspace method based on PCA was applied to speech signals in the time domain for noisy speech enhancement, and cepstral features from enhanced speech showed robustness in noisy speech recognition. ICA in [9] was applied to speech data in the time or time-frequency domain, and gave good performance in phoneme recognition tasks. In [10], LDA that was applied to speech data in the time-frequency domain showed better performance than combined linear discriminants in the temporal and spectral domain in continuous digit recognition task. Comparative experiment results using data-driven methods based on PCA, ICA, and LDA in phoneme recognition tasks were described in [11].
The effectiveness of these subspace-based methods has been confirmed in speech recognition or speech enhancement experiments, but it remains difficult to recognize observed speech in reverberant environments (e.g., [12–14]). If the impulse response of a room is longer than the length of short-time Discrete Fourier Transform (DFT), the effects of reverberation are both additive and multiplicative in the power spectrum domain [15]. Consequently, it becomes difficult to estimate the reverberant effects in the time or frequency domain. In [7], PCA was applied to speech signals in the logarithmic mel-frequency filter bank domain, and this approach showed robustness in distorted speech recognition. Therefore, we propose a new data-driven speech feature extraction method that we call the "Integrated Phoneme Subspace (IPS) method", which is based on [16] in the logarithmic mel-frequency filter bank domain.
Our method differs from conventional methods in that the proposed method attempts to incorporate phonemic information into the feature space. We apply PCA to estimate phoneme subspaces that are selected based on the Minimum Description Length (MDL) principle. Next, PCA or ICA is applied to integrate these phoneme subspaces. Speech feature vectors are obtained by transforming features linearly using a time-invariant transform matrix generated by our method. To evaluate our method, isolated word speech recognition experiments were performed. The proposed method provided higher recognition accuracy than conventional methods in clean and reverberant environments.
The content of this paper is as follows. In Section 2, we propose a new feature extraction method based on the subspace method, MDL-based subspace selection, and ICA. In Section 3, we describe our speech recognition experiments using the proposed method and discuss the results. Finally, conclusions are drawn in Section 4.
2. Proposed Method
Figure 1(a) is a block diagram that illustrates the speech feature extraction methods of MFCC and the proposed speech feature. The proposed feature is obtained by applying an IPS transform instead of DCT in the logarithmic mel-frequency filter bank domain. The IPS transform consists of two transforms: the projection onto phoneme subspaces and integration of phoneme subspaces, as shown in Figure 1(b). These two transforms are conducted by multiplying the feature vector by linear transform matrices.
2.1. Base Feature Extraction
To estimate the IPS transform matrix, we use logarithmic mel-frequency filter bank (called LogMFB) coefficients. As shown in Figure 1(b), speech signals are pre-emphasized by using a first-order FIR filter, and a stream of speech signals is segmented into a series of frames, with each frame windowed by a Hamming window. Next, applying FFT to each frame, the power spectra of time-series are obtained. The power spectra are filtered using a mel-frequency filter whose center frequency is spaced in mel scale and whose coefficients are weighted according to a triangular shape. Finally, the logarithms of MFB components are then computed based on the fact that the human auditory system is sensitive to speech loudness in the logarithmic scale.
2.2. Phoneme Subspaces Using PCA
To extract phonemic information from speech signals, we use the subspace method with Principal Component Analysis (PCA). PCA is defined as an orthogonal linear transformation that transforms data to a new coordinate system. This is also usually used for dimensionality reduction and decorrelation of feature coefficients. By applying PCA to each clean phoneme feature set, as shown in Figure 2, each respective phoneme subspace is obtained.
PCA is applied to each phoneme data matrix  that is a set of
that is a set of  -dimensional LogMFB vectors,
-dimensional LogMFB vectors,  , and those are randomly sampled from the frame set for each phoneme. The eigenvectors
, and those are randomly sampled from the frame set for each phoneme. The eigenvectors  that make the new coordinate system are computed by eigenvalue decomposition of the covariance matrix
that make the new coordinate system are computed by eigenvalue decomposition of the covariance matrix  as follows:
as follows:

Here  and
and  are a mean vector and an eigenvalue corresponding to the
are a mean vector and an eigenvalue corresponding to the  , respectively.
, respectively.
When an unknown vector  is inputted, by projecting the
is inputted, by projecting the  onto the
onto the  th phoneme subspace
th phoneme subspace  with
with  eigenvectors corresponding to the
eigenvectors corresponding to the  largest eigenvalues, a feature vector
largest eigenvalues, a feature vector  is defined, ignoring the constant term as follows:
is defined, ignoring the constant term as follows:

In the next subsection, the method of selecting the optimal dimension  of each phoneme subspace is described.
of each phoneme subspace is described.
Finally, the super-vector  is obtained by concatenating
is obtained by concatenating  as follows:
as follows:

Here,  indicates the number of phonemes and
indicates the number of phonemes and  is the matrix of the whole phoneme subspace defined as
is the matrix of the whole phoneme subspace defined as 
 . The dimensionality of
. The dimensionality of  ,
,  , is
, is

When a frame  of reverberant speech is inputted, the clean speech portion is projected onto subspace
of reverberant speech is inputted, the clean speech portion is projected onto subspace  . Then the reverberant portion projected onto
. Then the reverberant portion projected onto  , (complementary space of
, (complementary space of  ) is reduced as in [7]. The phoneme subspace estimate scheme is represented in Figure 2.
) is reduced as in [7]. The phoneme subspace estimate scheme is represented in Figure 2.
2.3. Optimal Phoneme Subspace Selection Based on MDL
The determination of the dimension for each phoneme subspace,  , requires the use of a truncation criterion. In [5], the MDL criterion was applied to the subspace selection problem in the case of noisy speech enhancement. Assuming that the redundancy of clean speech is additive white Gaussian in the logarithmic domain, the MDL criterion could be applied to clean speech data as follows:
, requires the use of a truncation criterion. In [5], the MDL criterion was applied to the subspace selection problem in the case of noisy speech enhancement. Assuming that the redundancy of clean speech is additive white Gaussian in the logarithmic domain, the MDL criterion could be applied to clean speech data as follows:

where  ,
,  , and
, and  are the dimension parameter, the selectivity of MDL, and the number of free parameters, respectively. We set
are the dimension parameter, the selectivity of MDL, and the number of free parameters, respectively. We set  then the optimal
then the optimal  is obtained as follows:
is obtained as follows:

This criterion provides both consistent and automatic phoneme subspace estimates.
2.4. Integration of Phoneme Subspaces
We made optimal phoneme subspaces and obtained feature vectors that enhance phonemic information from input speech signals. It should be noted that the aforementioned feature vectors are large dimension vectors (sum of each optimal phoneme subspace dimension), and some base vectors may correlate. It is efficient to reduce the dimension of the feature vector and to decorrelate components for speech recognition. For this purpose, we apply PCA or ICA to a set of feature  so that the integration matrix
so that the integration matrix  is obtained, as shown in Figure 3. This integration matrix is time-invariant and linear under the assumption that phoneme structures are time-invariant and are composed linearly of decorrelated components. Using the integration matrix
is obtained, as shown in Figure 3. This integration matrix is time-invariant and linear under the assumption that phoneme structures are time-invariant and are composed linearly of decorrelated components. Using the integration matrix  , our proposed speech feature vectors
, our proposed speech feature vectors  are generated as follows:
are generated as follows:

In our experiments, for a Hidden Markov Model (HMM)-based recognizer, we normalized  to zero mean and added the time derivatives to those normalized mean values so that the final dimensionality is
to zero mean and added the time derivatives to those normalized mean values so that the final dimensionality is  .
.
2.4.1. Integration Using PCA
As stated previously, PCA is able to reduce dimension and to decorrelate the components. Using eigenvalue decomposition of a covariance matrix of the data matrix  , eigenvalues and eigenvectors are obtained, nd by utilizing eigenvectors corresponding to the largest eigenvalues, we are able to construct an integration matrix
, eigenvalues and eigenvectors are obtained, nd by utilizing eigenvectors corresponding to the largest eigenvalues, we are able to construct an integration matrix  .
.
2.4.2. Integration Using ICA
Independent component analysis is a method for separating mutually independent source signals from mixed signals. In [9], ICA was used for speech feature extraction and phoneme recognition resulting in good recognition performance, and it is shown that the filter obtained by applying ICA to a speech data set in the time domain from a single microphone worked like a band-pass filter. Here, we use ICA for integrating phoneme subspaces.
A generative model of ICA is linear,  , where
, where  ,
,  , and
, and  are the observed data vector, mixing matrix, and source vector, respectively. By assuming that only the components of the source vector are mutually independent, an unmixing matrix
are the observed data vector, mixing matrix, and source vector, respectively. By assuming that only the components of the source vector are mutually independent, an unmixing matrix  (ideally
(ideally  ) and independent components
) and independent components  are estimated as follows
are estimated as follows  . The unmixing matrix
. The unmixing matrix  is estimated by maximizing the statistical independence of the estimated components. The statistical independence is usually represented by negentropy or kurtosis that is fourth-order cumulant, and maximization of statistical independence is implemented in a gradient algorithm or fixed-point algorithm.
is estimated by maximizing the statistical independence of the estimated components. The statistical independence is usually represented by negentropy or kurtosis that is fourth-order cumulant, and maximization of statistical independence is implemented in a gradient algorithm or fixed-point algorithm.
In this paper, we used FastICA [8] which is based on a fixed-point iteration scheme that maximizes negentropy. The FastICA algorithm for finding one  that derives one independent component is as follows.
that derives one independent component is as follows.
-
(1)
Center the data to make its mean zero.
-
(2)
Whiten the data to give
 .
. -
(3)
(3)Choose an initial (e.g., random) vector
 of unit norm.
of unit norm. -
(4)
Let
 where
where 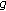 is the function that gives approximations of negentropy.
is the function that gives approximations of negentropy. -
(5)
Let
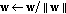 .
. -
(6)
If it is not converged, go back to step (4).
To estimate more independent components, different kinds of decorrelation schemes should be used; please refer to [8] for more information.
Applying ICA to the data matrix  , the independent components among phonemes are extracted and the dimensionality is compressed. The obtained unmixing matrix
, the independent components among phonemes are extracted and the dimensionality is compressed. The obtained unmixing matrix  is used for the integration matrix. The PCA integration matrix decorrelates the components, and the ICA integration matrix makes the components mutually independent.
is used for the integration matrix. The PCA integration matrix decorrelates the components, and the ICA integration matrix makes the components mutually independent.
3. Experiments
3.1. Experimental Conditions
In order to confirm the efficiency of the proposed method, the speech data were extracted from the A-set of the ATR Japanese database and the room impulse response was extracted from the RWCP sound scene database [17]. The total number of speakers was 10 (5 males and 5 females). The training data was composed of 2,620 utterances per speaker, and 1,000 clean or reverberant utterances made by convolving impulse responses [17] were used for testing each speaker. Table 1 shows the reverberant conditions.
Speech signals were digitized into 16 bits at a sampling frequency of 12 kHz. For spectral analysis, an ST-DFT was performed on 32-ms windowed and 8-ms shifted frames. Next, a 24-channel mel-frequency filter bank (MFB) analysis was performed on the aforementioned components. The logarithms of MFB components were then computed.
The experiments were conducted to compare 6 features, MFCC, PCA, ICA, LDA, IPS1, and IPS2, as follows.
-
(i)
MFCC: DCT to LogMFB vector
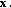
-
(ii)
PCA: apply PCA to a phoneme balanced set of LogMFB vectors.
-
(iii)
ICA: apply ICA to a phoneme balanced set of LogMFB vectors.
-
(iv)
LDA: apply LDA to a set of phoneme data matrices concurrently.
-
(v)
IPS1: apply PCA to a each phoneme data matrix
 and apply PCA to the data matrix
and apply PCA to the data matrix 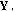
-
(vi)
IPS2: apply PCA to a each phoneme data matrix
 and apply ICA to the data matrix
and apply ICA to the data matrix 
Each phoneme data matrix  consisted of LogMFB vectors that were randomly selected and were less than 100 frames per speaker. In the case of PCA and ICA, the LogMFB vector set consisted of 5,072 frames that were equally extracted from the above phoneme data matrices. For IPS1 and IPS2, the sample size of
consisted of LogMFB vectors that were randomly selected and were less than 100 frames per speaker. In the case of PCA and ICA, the LogMFB vector set consisted of 5,072 frames that were equally extracted from the above phoneme data matrices. For IPS1 and IPS2, the sample size of  (
( ) was decided to be 5,336. The dimensions of the aforementioned features (
) was decided to be 5,336. The dimensions of the aforementioned features ( ) were set to 12 from 24 (
) were set to 12 from 24 ( ) for a fair comparison. The super-vector dimension (
) for a fair comparison. The super-vector dimension ( ) is described in the next subsection.
) is described in the next subsection.
As an acoustic model, the common HMMs of 54 ( ) context-independent phonemes were trained by using 10 sets of 2,620 clean words spoken by 10 speakers, respectively. Each HMM is left-right and has three states and three self-loops. Each state has 20 Gaussian mixture components. The LogMFB analysis, training phoneme HMMs, and testing were realized by using HTK toolkits [18].
) context-independent phonemes were trained by using 10 sets of 2,620 clean words spoken by 10 speakers, respectively. Each HMM is left-right and has three states and three self-loops. Each state has 20 Gaussian mixture components. The LogMFB analysis, training phoneme HMMs, and testing were realized by using HTK toolkits [18].
3.2. Results and Discussions
3.2.1. MDL-Based Phoneme Subspace Selection
Table 2 shows the results of the MDL-based phoneme subspace selection. LogMFB vectors are projected onto each of the optimal phoneme subspaces. It is confirmed that the dimensions of vowels are larger than those of consonants. In particular, vowel  has the largest (10) dimension and consonant
has the largest (10) dimension and consonant  the smallest (2) dimension. This trend means that phoneme subspaces have correlated information between each other. In order to improve efficiency, this correlation should be reduced.
the smallest (2) dimension. This trend means that phoneme subspaces have correlated information between each other. In order to improve efficiency, this correlation should be reduced.
Figure 4 shows isolated word speech recognition results with IPS1. This experiment compares manual phoneme subspace selection to MDL-based selection. Manual phoneme subspace selection means that all phoneme subspaces have the same dimension ( ) by selecting the eigenvectors corresponding 8, 10, 12, or 14 largest eigenvalues. However, in the case of MDL-based selection,
) by selecting the eigenvectors corresponding 8, 10, 12, or 14 largest eigenvalues. However, in the case of MDL-based selection,  is decided independently of each phoneme. The dimension of
is decided independently of each phoneme. The dimension of  ,
,  , was 373 based on the MDL principle. While the best manual selection varies according to the conditions, the MDL-based subspace selection provided the best performance in all conditions, except for the case of 10 dimensions in the 380 ms reverberant condition. From this result, it is shown that MDL-based subspace selection provides good performance without adjusting subspace dimension manually.
, was 373 based on the MDL principle. While the best manual selection varies according to the conditions, the MDL-based subspace selection provided the best performance in all conditions, except for the case of 10 dimensions in the 380 ms reverberant condition. From this result, it is shown that MDL-based subspace selection provides good performance without adjusting subspace dimension manually.
3.2.2. Isolated Word Speech Recognition
Figure 5 shows the obtained recognition accuracy. The speaker independent HMMs are trained by clean speech data. The recognition accuracy is the average of the 10 speakers. The ICA-based features (ICA, IPS2) refer to the average of three experimental results for the different initial values of  . The standard deviations were 0.25 (clean), 0.67 (380 ms), and 1.01 (600 ms) in the case of ICA, and 0.2, 0.9, and 3.0 in the case of IPS2, respectively. As the reverberation time lengthens, the standard deviation increases.
. The standard deviations were 0.25 (clean), 0.67 (380 ms), and 1.01 (600 ms) in the case of ICA, and 0.2, 0.9, and 3.0 in the case of IPS2, respectively. As the reverberation time lengthens, the standard deviation increases.
MFCC shows the worst performance in all conditions. The PCA-based methods (PCA, IPS1) show the highest recognition accuracy (96.9 ) under clean conditions. In reverberant conditions, the recognition accuracy decreases markedly. However, the proposed methods (IPS1 and IPS2) show better results than conventional methods.
) under clean conditions. In reverberant conditions, the recognition accuracy decreases markedly. However, the proposed methods (IPS1 and IPS2) show better results than conventional methods.
ICA-based methods overall show a lower performance than PCA-based methods, especially under clean conditions. In this paper, we used a Gaussian mixture model (GMM) on each state of HMM. However, this acoustic model is not exactly advisable to exploit the independence of ICA components, because each distribution of independent component obtained by ICA is non-Gaussian [8]. Changing this acoustic model for the independent components may achieve an increase in recognition accuracy, as described in [19], which proposed a method using Factor Analysis (FA) for both feature extraction and acoustic modeling.
Although we used a FastICA algorithm to integrate phoneme subspaces, we believe that the results do not differ in comparison to the use of other ICA algorithms such as the joint approximate diagonalization of eigenmatrices (JADEs) algorithm or Infomax algorithm [20].
4. Conclusions
We proposed the new speech feature extraction method which emphasizes the phonemic information from observed speech using PCA, the MDL principle, and ICA. The proposed feature is obtained by transform matrices that are linear and time-invariant. The MDL-based phoneme subspace selection experiment confirmed that optimal subspace dimensions differ. The experiment results in isolated word recognition under clean and reverberant conditions showed that the proposed method outperforms conventional MFCC. The proposed method can be combined with other methods, such as speech signal processing or model adaptation, to improve the recognition accuracy in real-life environments. Further research is needed to find appropriate acoustic modeling methods for the independent components, to confirm the effectiveness of the proposed method in other noisy environments, and to adapt nonlinear transformation methods.
References
Hermansky H, Morgan N: RASTA processing of speech. IEEE Transactions on Speech and Audio Processing 1994,2(4):578-589. 10.1109/89.326616
Kingsbury BED, Morgan N: Recognizing reverberant speech with RASTA-PLP. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '97), April 1997, Munich, Germany 2: 1259-1262.
Avendano C, Tivrewala S, Hermansky H: Multiresolution channel normalization for ASR in reverberant environments. Proceedings of the 6th European Conference on Speech Communication and Technology (Eurospeech '97), September 1997, Rhodes, Greece 1107-1110.
Gelbart D, Morgan N: Evaluating long-term spectral subtraction for reverberant ASR. Proceedings of IEEE Automatic Speech Recognition and Understanding Workshop (ASRU '01), December 2001, Madonna di Campiglio, Italy 103-106.
Vetter R, Virag N, Renevey P, Vesin J-M: Single channel speech enhancement using principal component analysis and MDL subspace selection. Proceedings of the 6th European Conference on Speech Communication and Technology (Eurospeech '99), September 1999, Budapest, Hungary 2411-2414.
Hermus K, Wambacq P, Van Hamme H: A review of signal subspace speech enhancement and its application to noise robust speech recognition. EURASIP Journal on Advances in Signal Processing 2007, Article ID 45821 15 Pages 2007:.
Takiguchi T, Ariki Y: PCA-based speech enhancement for distorted speech recognition. Journal of Multimedia 2007,2(5):13-18.
Hyvärinen A, Oja E: Independent component analysis: algorithms and applications. Neural Networks 2000,13(4-5):411-430. 10.1016/S0893-6080(00)00026-5
Kwon O-W, Lee T-W: Phoneme recognition using ICA-based feature extraction and transformation. Signal Processing 2004,84(6):1005-1019. 10.1016/j.sigpro.2004.03.004
Kajarekar SS, Yegnanarayana B, Hermansky H: A study of two dimensional linear discriminants for ASR. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '01), May 2001, Salt Lake, Utah, USA 1: 137-140.
Somervuo P: Experiments with linear and nonlinear feature transformations in HMM based phone recognition. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '03), April 2003, Hong kong 1: 52-55.
Kinoshita K, Nakatani T, Miyoshi M: Spectral subtraction steered by multi-step forward linear prediction for single channel speech dereverberation. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '06), May 2006, Toulouse, France 1: 817-820.
Toh AM, Togneri R, Nordholm S: Feature and distribution normalization schemes for statistical mismatch reduction in reverberant speech recognition. Proceedings of the 8th Annual Conference of the International Speech Communication Association (Interspeech '07), August 2007, Antwerp, Belgium 234-237.
Petrick R, Lu X, Unoki M, Akagi M, Hoffmann R: Robust front end processing for speech recognition in reverberant environments: utilization of speech characteristics. Proceedings of the Annual Conference of the International Speech Communication Association (Interspeech '08), September 2008, Brisbane, Australia 658-661.
Gomez R, Even J, Saruwatari H, Shikano K: Distant-talking robust speech recognition using late reflection components of room impulse response. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '08), March-April 2008, Las Vegas, Nev, USA 4581-4584.
Park H, Takiguchi T, Ariki Y: Integration of phoneme-subspaces using ICA for speech feature extraction and recognition. Proceedings of Hands-Free Speech Communication and Microphone Arrays (HSCMA '08), May 2008, Trento, Italy 148-151.
Nakamura S, Hiyane K, Asano F, Nishimura T, Yamada T: Acoustical sound database in real environments for sound scene understanding and hands-free speech recognition. Proceedings of the 2nd International Conference on Language Resources and Evaluation (LREC '00), May-June 2000, Athens, Greece 2: 965-968.
Young S, Evermann G, Gales M, et al.: The HTK Book (for HTK Version 3.4). Cambridge University, Cambridge, UK; 2006.
Ting C-W, Chien J-T: Factor analysis of acoustic features for streamed hidden Markov modeling. Proceedings of IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU '07), December 2007, Kyoto, Japan 30-35.
Amari S: Neural learning in structured parameter spaces—natural Riemannian gradient. In Advances in Neural Information Processing System. Volume 9. MIT Press, Cambridge, Mass, USA; 1997:127-133.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Park, H., Takiguchi, T. & Ariki, Y. Integrated Phoneme Subspace Method for Speech Feature Extraction. J AUDIO SPEECH MUSIC PROC. 2009, 690451 (2009). https://doi.org/10.1155/2009/690451
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/690451



 .
. of unit norm.
of unit norm. where
where 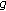 is the function that gives approximations of negentropy.
is the function that gives approximations of negentropy.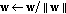 .
.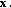
 and apply PCA to the data matrix
and apply PCA to the data matrix 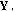
 and apply ICA to the data matrix
and apply ICA to the data matrix 

