- Research Article
- Open access
- Published:
Combining Superdirective Beamforming and Frequency-Domain Blind Source Separation for Highly Reverberant Signals
EURASIP Journal on Audio, Speech, and Music Processing volume 2010, Article number: 797962 (2010)
Abstract
Frequency-domain blind source separation (BSS) performs poorly in high reverberation because the independence assumption collapses at each frequency bins when the number of bins increases. To improve the separation result, this paper proposes a method which combines two techniques by using beamforming as a preprocessor of blind source separation. With the sound source locations supposed to be known, the mixed signals are dereverberated and enhanced by beamforming; then the beamformed signals are further separated by blind source separation. To implement the proposed method, a superdirective fixed beamformer is designed for beamforming, and an interfrequency dependence-based permutation alignment scheme is presented for frequency-domain blind source separation. With beamforming shortening mixing filters and reducing noise before blind source separation, the combined method works better in reverberation. The performance of the proposed method is investigated by separating up to 4 sources in different environments with reverberation time from 100 ms to 700 ms. Simulation results verify the outperformance of the proposed method over using beamforming or blind source separation alone. Analysis demonstrates that the proposed method is computationally efficient and appropriate for real-time processing.
1. Introduction
The objective of acoustic source separation is to estimate original sound sources from the mixed signals. This technique has found a lot of applications in noise-robust speech recognition and high-quality hands-free telecommunication systems. A classical example is to separate audio sources observed in a real room, known as a cocktail party environment, where a number of people are talking concurrently. A lot of research has focused on the problem but development is currently still in progress. Two kinds of techniques are promising in achieving source separation with multiple microphones: beamforming and blind source separation.
Beamforming is a technique used in sensor array for directional signal reception [1, 2]. Based on a model of the wavefront from acoustic sources, it can enhance target direction and suppress unwanted ones by coherently summing signals from the sensors. Beamforming can be classified as either fixed beamforming or adaptive one, depending on how the beamformer weights are chosen. The weights of a fixed beamformer do not depend on array data and are chosen to present a specified response for all scenarios. The most conventional fixed beamformer is a delay-and-sum one, which however requires a large number of microphones to achieve high performance. Another filter-and-sum beamformer has superdirectivity response with optimized weights. The weights of an adaptive beamformer are chosen based on the statistics of array data to optimize array response. In source separation system, each source signals may be separately obtained using the directivity of the array if the directions of sources are known. However, beamforming has limited performance in highly reverberant conditions because it can not suppress the interfering reverberation coming from the desired direction.
Blind source separation (BSS) is a technique for recovering the source signals from observed signals with the mixing process unknown [3]. It just relies on the independence assumption of source signals to estimate them from the mixtures. The cocktail party problem is a challenge because the mixing process is convolutive, where the observations are combinations of filtered versions of sources. A large number of unmixing filter coefficients should be calculated simultaneously to recover the original signals. The convolutive BSS problem can be solved in the time domain or the frequency domain [4]. In time domain BSS, the separation network is derived by optimizing a time-domain cost function [5–7]. However, these approaches may not be effective due to slow convergence and large computational load. In frequency-domain BSS, the observed time-domain signals are converted into the time-frequency domain by short-time Fourier transform (STFT); then instantaneous BSS is applied to each frequency bin, after which the separated signals of all frequency bins are combined and inverse-transformed to the time domain [8, 9]. Although satisfactory instantaneous separation may be achieved within all frequency bins, combining them to recover the original sources is a challenge because of the unknown permutations associated with individual frequency bins. This is the permutation ambiguity problem. There are two common strategies to solve this problem. The first strategy is to exploit the interfrequency dependence of separated signals [10, 11]. The second strategy is to exploit the position information of sources such as direction of arrival [12, 13]. By analyzing the directivity pattern formed by a separation matrix, source direction can be estimated and permutations aligned. Generally these two strategies can be combined to get a better permutation alignment [14].
Besides the permutation problem, another fundamental problem also limits the performance of frequency-domain BSS: the dilemma in determining the STFT analysis frame length [15–17]. Frames shorter than mixing filters generate incomplete instantaneous mixtures, while long frames collapse the independence measure at each frequency bin and disturb separation. The conflict is even severer in high reverberation with long mixing filters. Generally, a frequency-domain BSS which works well in low (100–200 ms) reverberation has degraded performance in medium (200–500 ms) and high ( 500 ms) reverberation. Since the problem originates from a processing step, which approximates linear convolutions with circular convolutions, in frequency-domain BSS, we call it "circular convolution approximation problem". This problem will be further elaborated in Section 2.2. Although great progress has been made for the permutation problem in recent years, few methods have been proposed with good separation results in a highly reverberant environment.
500 ms) reverberation. Since the problem originates from a processing step, which approximates linear convolutions with circular convolutions, in frequency-domain BSS, we call it "circular convolution approximation problem". This problem will be further elaborated in Section 2.2. Although great progress has been made for the permutation problem in recent years, few methods have been proposed with good separation results in a highly reverberant environment.
To improve the separation performance in high reverberation, this paper proposes a method which combines beamforming and blind source separation. Assuming the sound source locations are known, the proposed method employs beamforming as a preprocessor for blind source separation. With beamforming reducing reverberation and enhancing signal-to-noise ratio, blind source separation works well in reverberant environments, and thus the combined method performs better than using either of the two methods alone. Since the proposed method requires the knowledge of source locations for beamforming, it is a semiblind method. However, the source locations may be estimated with an array sound source localization algorithm or using other approaches, which is beyond the scope of this paper [18, 19].
In fact, the relationship between blind source separation and beamforming has been intensively investigated in recent years, and adaptive beamforming is commonly used to explain the physical principle of convolutive BSS [15, 20]. In addition, many approaches have been presented that combine both techniques. Some of these combined approaches are aimed at resolving the permutation ambiguity inherent in frequency-domain BSS [12, 21], whereas other approaches utilize beamforming to provide a good initialization for BSS or to accelerate its convergence [22–24]. So far as we know, there were no systematically studies on a direct application of the BSS-beamforming combination to high reverberant environments.
The rest of paper is organized as follows. Frequency-domain BSS and its circular convolution approximation problem are introduced in Section 2. The proposed method combining BSS and beamforming is presented in Section 3. Section 4 gives experimental results in various reverberant environments. Finally conclusions are drawn in Section 5.
2. Frequency-Domain BSS and Its Fundamental Problem
2.1. Frequency-Domain BSS
Supposing  sources and
sources and  sensors in a real-world acoustic scenario, the source vector
sensors in a real-world acoustic scenario, the source vector  , and the observed vector
, and the observed vector  , the mixing channels can be modeled by FIR filters of length
, the mixing channels can be modeled by FIR filters of length  , the convolutive mixing process is formulated as
, the convolutive mixing process is formulated as

where  is a sequence of
is a sequence of  matrices containing the impulse responses of the mixing channels, and the operator "*" denotes matrix convolution. For separation, we use FIR filters of length
matrices containing the impulse responses of the mixing channels, and the operator "*" denotes matrix convolution. For separation, we use FIR filters of length  and obtain estimated source signal vector
and obtain estimated source signal vector  by
by

where  is a sequence of
is a sequence of  matrices containing the unmixing filters, and the operator "*" denotes matrix convolution.
matrices containing the unmixing filters, and the operator "*" denotes matrix convolution.
The unmixing network  can be obtained by a frequency-domain BSS approach. After transforming the signals to the time-frequency domain using blockwise
can be obtained by a frequency-domain BSS approach. After transforming the signals to the time-frequency domain using blockwise  -point short-time Fourier transform (STFT), the convolution becomes a multiplication
-point short-time Fourier transform (STFT), the convolution becomes a multiplication

where  is a decimated version of the time index
is a decimated version of the time index  ,
,  is the STFT of
is the STFT of  ,
,  is the Fourier transforms of
is the Fourier transforms of  , and
, and  is the frequency.
is the frequency.
The frequency-domain BSS makes an assumption that the time series at each bin are mutual independent. It is possible to separate them using complex-valued instantaneous BSS algorithms such as FastICA [25] and Infomax [26, 27], which are considered to be quite mature. However, there are scaling and permutation ambiguities at each bin. This is expressed as

where  is the STFT of
is the STFT of  ,
,  is the Fourier transform of
is the Fourier transform of  ;
;  is a permutation matrix and
is a permutation matrix and  a scaling matrix, all at frequency
a scaling matrix, all at frequency  . The source permutation and gain indeterminacy are problems inherent in frequency-domain BSS. It is necessary to correct them before transforming the signals back to the time domain.
. The source permutation and gain indeterminacy are problems inherent in frequency-domain BSS. It is necessary to correct them before transforming the signals back to the time domain.
Finally the unmixing network  is obtained by inverse Fourier transforming
is obtained by inverse Fourier transforming  , and the estimated source
, and the estimated source  is obtained by filtering
is obtained by filtering  through
through  . The workflow of the frequency-domain BSS is shown in Figure 1.
. The workflow of the frequency-domain BSS is shown in Figure 1.
2.2. Circular Convolution Approximation Problem
Besides permutation and scaling ambiguities, another problem also affects the performance of frequency-domain BSS: the STFT circular convolution approximation. In the frequency domain, the convolutive mixture is reduced to an instantaneous mixture for each frequency bin. The model (3) is simple but generates two errors for short STFT analysis frame length  [16].
[16].
-
(1)
The STFT covers only
 samples of the impulse response
samples of the impulse response 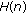 , not its entirety.
, not its entirety. -
(2)
Equation (3) is only an approximation since it implies a circular convolution but not a linear convolution in the time domain; it is correct only when the mixing filter length
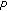 is short compared to
is short compared to 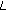 .
.
As a result, it is necessary to work with  to ensure the accuracy of (3). However in that case, the instantaneous separation performance is saturated before reaching a sufficient separation, because decreased time resolution for STFT and fewer data available in each frequency bin will collapse the independence assumption and deteriorate instantaneous separation [15, 17].
to ensure the accuracy of (3). However in that case, the instantaneous separation performance is saturated before reaching a sufficient separation, because decreased time resolution for STFT and fewer data available in each frequency bin will collapse the independence assumption and deteriorate instantaneous separation [15, 17].
In a nutshell, short frames make the conversion to instantaneous mixture incomplete, while long ones disturb the separation. This contradiction is even severer in highly reverberant environments, where the mixing filters are much longer than STFT analysis frame. This is the reason for the poor performance of frequency-domain BSS in high reverberation.
It is necessary to work with  to ensure the accuracy of (3). In this case, however, long frames worsen time resolution in the time-frequency domain and decrease the number of samples in each bin. As the result, the independence of source signals decreases greatly at some bins, leading to deteriorated instantaneous BSS and hence significantly reducing convolutive BSS performance in high reverberation [15, 17]. In other words, short frames make the conversion to instantaneous mixture incomplete, while long ones disturb the separation. The conflict becomes severer in highly reverberant environments and lead to the degraded performance.
to ensure the accuracy of (3). In this case, however, long frames worsen time resolution in the time-frequency domain and decrease the number of samples in each bin. As the result, the independence of source signals decreases greatly at some bins, leading to deteriorated instantaneous BSS and hence significantly reducing convolutive BSS performance in high reverberation [15, 17]. In other words, short frames make the conversion to instantaneous mixture incomplete, while long ones disturb the separation. The conflict becomes severer in highly reverberant environments and lead to the degraded performance.
3. Combined Separation Method
Based on the analysis above, the circular convolution approximation problem seriously degrades the separation performance in high reverberation. However, the problem may be mitigated if the mixing filters become shorter. With directive response enhancing desired direction and suppress unwanted ones, beamforming can deflates the reflected paths and hence shorten the mixing filter indirectly. It thus may help compensate for the deficiency of blind source separation. From another point of view, beamforming makes primary use of spatial information while blind source separation utilizes statistical information contained in signals. Integrating both pieces of information should help get better separation results, just like the way our ears separate audio signal [28]. In summary, if we use beamforming as a preprocessor for blind source separation, at least three advantages can be achieved.
-
(1)
The interfering residuals due to reverberation after beamforming are further reduced by blind source separation.
-
(2)
The poor separation performance of blind source separation in reverberant environments is compensated for by beamforming, which suppresses the reflected paths and shortens the mixing filters;
-
(3)
Beamformer enhances the source in its path and suppresses the ones outside. It thus enhances signal-to-noise ratio and provides a cleaner output for blind source separation to process.
Assuming source directions are known, we propose a combined method as illustrated in Figure 2. For  sources received by an array of
sources received by an array of  microphones,
microphones,  beams are formed towards them, respectively. Then the
beams are formed towards them, respectively. Then the  beamformed outputs are fed to blind separation to recover the
beamformed outputs are fed to blind separation to recover the  sources. The workflow of the proposed method is shown in Figure 3.
sources. The workflow of the proposed method is shown in Figure 3.
The mixing stage is expressed as

where  is the source vector,
is the source vector,  is the observed vector,
is the observed vector,  is a sequence of
is a sequence of  matrices containing the impulse responses of the mixing channels, and the operator "*" denotes matrix convolution.
matrices containing the impulse responses of the mixing channels, and the operator "*" denotes matrix convolution.
The beamforming stage is expressed as

where  is the beamforming output vector,
is the beamforming output vector,  is the observed vector,
is the observed vector,  is a sequence of
is a sequence of  matrices containing the impulse responses of beamformer,
matrices containing the impulse responses of beamformer,  is the global impulse response by combining
is the global impulse response by combining  and
and  , and the operator "*" denotes matrix convolution.
, and the operator "*" denotes matrix convolution.
The blind source separation stage is expressed as

where  is the estimated source signal vector,
is the estimated source signal vector,  is a sequence of
is a sequence of  matrices containing the unmixing filters, and the operator "*" denotes matrix convolution.
matrices containing the unmixing filters, and the operator "*" denotes matrix convolution.
It can be seen from (5)–(7) that, with beamforming reducing reverberation and enhancing signal-to-noise ratio, the combined method is able to replace the original mixing network  , which results from the room impulse response, with a new mixing network
, which results from the room impulse response, with a new mixing network  , which is easier to separate.
, which is easier to separate.
Regarding the implementation detail, two techniques are employed: superdirective beamformer, which can fully exert the dereverberation and noise reduction ability of a microphone array, and frequency-domain blind source separation, which is well known for its fast convergence and small computation. These two issues will be addressed as below.
3.1. Beamforming
Beamformer can be implemented as a fixed one or an adaptive one. Compared to fixed beamforming, an adaptive method is not appropriate for the combined method. The reasons are as follows.
-
(1)
An adaptive beamformer obtains directive response mainly by analyzing the statistical information contained in the array data, not by utilizing the spatial information directly. Its essence is similar to that of convolutive blind source separation [15]. Cascading them together is equivalent to using the same techniques repeatedly, hence contributing little to performance improvement.
-
(2)
An adaptive beamformer generally adapts its weights during breaks in the target signal [1]. However, it is a challenge to predict signal breaks when several people are talking concurrently. This significantly limits the applicability of adaptive beamforming to source separation.
In contrast, a fixed beamformer, which relies mainly on spatial information, does not have such disadvantages. It is data-independent and more stable. Given a look direction, the directive response is obtained for all scenarios. Thus a fixed beamformer is preferred in the proposed method.
Fixed beamforming achieves a directional response by coherently summing signals from multiple sensors based on a model of the wavefront from acoustic sources. The most common beamformer is the delay-and-sum one, however, a filter-and-sum beamformer has superdirectivity response with optimized weights. Its principle is given in Figure 4. The beamformer produces a weighted sum of signals from  sensors to enhance the target direction [29]. A frequency-domain method is employed to design the superdirective beamformer.
sensors to enhance the target direction [29]. A frequency-domain method is employed to design the superdirective beamformer.
Suppose a beamformer model with a target source  and background noise
and background noise  , the components received by the
, the components received by the  th sensor is
th sensor is  in the time domain. Similarly, in the frequency domain, the
in the time domain. Similarly, in the frequency domain, the  th sensor output is
th sensor output is  . The array output in the frequency domain is
. The array output in the frequency domain is

where  is the beamforming weight vector composed of beamforming weights from each sensor, and
is the beamforming weight vector composed of beamforming weights from each sensor, and  is the output vector composed of outputs from each sensor, and
is the output vector composed of outputs from each sensor, and  denotes conjugate transpose. The
denotes conjugate transpose. The  depends on the array geometry and source directivity, as well as the array output optimization criterion such as a signal-to-noise ratio (SNR) gain criterion [29–31].
depends on the array geometry and source directivity, as well as the array output optimization criterion such as a signal-to-noise ratio (SNR) gain criterion [29–31].
Suppose  is the source vector which is composed of the target source signals from the sensors, and
is the source vector which is composed of the target source signals from the sensors, and  is the noise vector which is composed of the spatial diffuse noises from the sensors. The array gain is a measure of the improvement in signal-to-noise ratio. It is defined as the ratio of the SNR at the output of the beamforming array to the SNR at a single reference microphone. For development of the theory, the reference SNR is defined, as in [29], to be the ratio of average signal power spectral densities over the microphone array,
is the noise vector which is composed of the spatial diffuse noises from the sensors. The array gain is a measure of the improvement in signal-to-noise ratio. It is defined as the ratio of the SNR at the output of the beamforming array to the SNR at a single reference microphone. For development of the theory, the reference SNR is defined, as in [29], to be the ratio of average signal power spectral densities over the microphone array,  , to the average noise-power spectral density over the array,
, to the average noise-power spectral density over the array,  . By derivation, the array gain at frequency
. By derivation, the array gain at frequency  is expressed as
is expressed as

where  is the normalized signal cross-power spectral density matrix, and
is the normalized signal cross-power spectral density matrix, and  is the normalized noise cross-power spectral density matrix. Provided
is the normalized noise cross-power spectral density matrix. Provided  is nonsingular, the array gain is maximized with the weight vector
is nonsingular, the array gain is maximized with the weight vector

The terms  and
and  in (10) depend on the array geometry and the target source direction. For a circular array, the calculation of
in (10) depend on the array geometry and the target source direction. For a circular array, the calculation of  and
and  is given as follows [2].
is given as follows [2].
Figure 5 shows an  -element circular array with a radius of
-element circular array with a radius of  and a target source coming from the direction
and a target source coming from the direction  . The elements are equally spaced around the circumference, and their positions, which are determined from the layout of array, are given in the matrix form as
. The elements are equally spaced around the circumference, and their positions, which are determined from the layout of array, are given in the matrix form as

The source vector  can be derived as
can be derived as

where  is the wave number, and
is the wave number, and  is the sound velocity. And the normalized noise cross-power spectral density matrix
is the sound velocity. And the normalized noise cross-power spectral density matrix  is expressed as
is expressed as

where  is the
is the  entry of the matrix
entry of the matrix  ,
,  is the wave number,
is the wave number,  is the distance between two microphones
is the distance between two microphones  and
and 

After calculating the beamforming vector by (10), (12) and (13) at each frequency bin, the time-domain beamforming filter  is obtained by inverse Fourier transforming
is obtained by inverse Fourier transforming  .
.
The procedure above is to design a beamformer with only one target direction. For  sources with known directions,
sources with known directions,  beams are designed pointing at them, respectively. Finally, supposing the observed vector at
beams are designed pointing at them, respectively. Finally, supposing the observed vector at  sensors is
sensors is  , the multiple beamforming is formulated as
, the multiple beamforming is formulated as

where  is a sequence of
is a sequence of  matrices containing the impulse responses of the beamformer,
matrices containing the impulse responses of the beamformer,  is length of the beamforming filter, and
is length of the beamforming filter, and  is the beamformed output vector.
is the beamformed output vector.
3.2. Frequency-Domain Blind Source Separation
As discussed before, the workflow of frequency-domain blind source separation is shown in Figure 1. Three realization details will be addressed: instantaneous BSS, permutation alignment, and scaling correction.
3.2.1. Instantaneous BSS
After decomposing time-domain convolutive mixing into frequency-domain instantaneous mixing, it is possible to perform separation at each frequency bin with a complex-valued instantaneous BSS algorithm. Here we use Scaled Infomax algorithm, which is not sensitive to initial values, and is able to converge to the optimal solution within 100 iterations [32].
3.2.2. Permutation Alignment
Permutation ambiguity inherent in frequency-domain BSS is a challenge in the combined method. Generally, there are two approaches to cope with the permutation problem. One is to exploit the dependence of separated signals across frequencies. Another is to exploit the position information of sources: the directivity pattern of the mixing/unmixing matrix provides a good reference for permutation alignment. However, in the combined method, the directivity information contained in the mixing matrix does not exist any longer after beamforming. Even if the source positions are known, they are not much helpful for permutation alignment. Consequently, what we can use for permutation is merely the first reference: the interfrequency dependence of separated signals. In [33] we have proposed a permutation alignment approach with good results, which is based on an interfrequency dependence measure: the powers of separated signals. Its principle is briefly given as below.
An interfrequency dependence measure, the correlation coefficient of separated signal power ratios, exhibits a clearer interfrequency dependence among all frequencies. Suppose the  mixing network at frequency
mixing network at frequency  can be estimated from the separation network by
can be estimated from the separation network by

where  is the
is the  th column vector of
th column vector of  ,
,  denotes inversion of a square matrix or pseudoinversion of a rectangular matrix. The power ratio, which measures the dominance of the
denotes inversion of a square matrix or pseudoinversion of a rectangular matrix. The power ratio, which measures the dominance of the  th separated signal in the observations at frequency
th separated signal in the observations at frequency  , is defined, as in [11], to be
, is defined, as in [11], to be

where the denominator is the total power of the observed signals  , the numerator is the power of the
, the numerator is the power of the  th separated signal, and
th separated signal, and  is the
is the  th component of the separated signal
th component of the separated signal  , that is,
, that is,  . Being in the range
. Being in the range  , (17) is close to 1 when the
, (17) is close to 1 when the  th separated signal is dominant, and close to 0 when others are dominant. The power ratio measure can clearly exhibit the signal activity due to the sparsity of speech signals.
th separated signal is dominant, and close to 0 when others are dominant. The power ratio measure can clearly exhibit the signal activity due to the sparsity of speech signals.
The correlation coefficient of signal power ratios can be used for measuring interfrequency dependence and solving the permutation problem. The normalized binwise correlation coefficient between two power ratio sequences  and
and  is defined as
is defined as

where  and
and  are indices of two separated channels,
are indices of two separated channels,  and
and  are two frequencies,
are two frequencies,  ,
,  ,
,  are, respectively, the correlation, mean, and standard deviation at time
are, respectively, the correlation, mean, and standard deviation at time  (The time index
(The time index  is omitted for clarity). Note that
is omitted for clarity). Note that  denotes expectation. Being in the range
denotes expectation. Being in the range  , (18) tends to be high if the output channels
, (18) tends to be high if the output channels  and
and  originate from the same source and low if they represent different sources. This property will be used for aligning the permutation.
originate from the same source and low if they represent different sources. This property will be used for aligning the permutation.
Reference [33] has proposed a permutation alignment approach based on the power ratio measure. Binwise permutation alignment is applied first across all frequency bins, using the correlation of separated signal powers; then the full frequency band is partitioned into small regions based on the binwise permutation alignment result. Finally, regionwise permutation alignment is performed, which can prevent the spreading of the misalignment at isolated frequency bins to others and thus improves permutation. This permutation alignment approach is employed in the proposed method.
3.2.3. Scaling Correction
The scaling indeterminacy can be resolved relatively easily by using the Minimal Distortion Principle [34]:

where  is
is  after permutation correction and
after permutation correction and  is the one after scaling correction,
is the one after scaling correction,  denotes inversion of a square matrix or pseudoinversion of a rectangular matrix;
denotes inversion of a square matrix or pseudoinversion of a rectangular matrix;  retains only the main diagonal components of the matrix.
retains only the main diagonal components of the matrix.
3.3. Computational Complexity Analysis
The coefficients of the beamformer filters can be calculated off line and stored previously. Thus compared a BSS-only method, the combined method just increases the number of calculations slightly. The computation of the combined method is composed of three parts: beamforming filtering, separation filter estimation, and unmixing filtering. Suppose there are  sources and
sources and  microphones, the length of the input signals is
microphones, the length of the input signals is  , the number of iterations for Scaled Infomax algorithm is
, the number of iterations for Scaled Infomax algorithm is  , the filter length of the beamformer is
, the filter length of the beamformer is  , and the length of the unmixing filter is
, and the length of the unmixing filter is  . The beamforming filtering and unmixing filtering can be implemented by FFT. The computation cost of the proposed algorithm is summarized in Table 1. (The computation cost of separation filter estimation is given in [33].) For convenience, only complex-valued multiplication operations are considered.
. The beamforming filtering and unmixing filtering can be implemented by FFT. The computation cost of the proposed algorithm is summarized in Table 1. (The computation cost of separation filter estimation is given in [33].) For convenience, only complex-valued multiplication operations are considered.
To summarize, the total computation cost for the  input data points is
input data points is

The average computation for each sample time with  input data points is
input data points is

We think the result is quite acceptable. For 4 sources recorded by a 16-element microphone array,  ,
,  , the average computation involves about 7200 complex-valued multiplications for each sample time (with 16 sample points). Thus, in terms of computational complexity, the proposed algorithm is promising for real-time applications.
, the average computation involves about 7200 complex-valued multiplications for each sample time (with 16 sample points). Thus, in terms of computational complexity, the proposed algorithm is promising for real-time applications.
4. Experiment Results and Analysis
We evaluate the performance of the proposed method in simulated experiments in two parts. The first part verifies the dereverberation performance of beamforming. The second investigates the performance of the proposed method in various reverberant conditions, and compares it with a BSS-only method and a beamforming-only one.
The implementation detail of the algorithm is as follows. For blind source separation, the Tukey window is used in STFT, with a shift size of 1/4 window length. The iteration number of instantaneous Scaled Infomax algorithm is 100. The processing bandwidth is between 100 and 3750 Hz (sampling rate being 8 kHz). The STFT frame size will vary according to different experimental conditions. For beamforming, a circular microphone array is used to design the beamformer with the filter length 2048, the array size will vary according to different experimental conditions.
4.1. Simulation Environment and Evaluation Measures
The simulation environment is shown in Figure 6, the room size is  , all sources and microphones are 1.5 m high. The room impulse response was obtained by using the image method [35], and the reverberation time was controlled by varying the absorption coefficient of the wall.
, all sources and microphones are 1.5 m high. The room impulse response was obtained by using the image method [35], and the reverberation time was controlled by varying the absorption coefficient of the wall.
The separation performance is measured by signal-to-interference ratio (SIR) in dB.
Before beamforming, the input SIR of the  th channel is
th channel is

where  is the total number of microphones,
is the total number of microphones,  denotes the norm-2 operation,
denotes the norm-2 operation,  is an element of the mixing system
is an element of the mixing system  (see (1)).
(see (1)).
After beamforming, the SIR of the  th channel is
th channel is

where  is the total number of beams,
is the total number of beams,  is an element of
is an element of  , the combined impulse response matrix from the mixing system
, the combined impulse response matrix from the mixing system  and the bamforming system
and the bamforming system  .
.
After blind source separation, the SIR of the  th channel is
th channel is

where  is the total number of sources,
is the total number of sources,  is an element of
is an element of  , the overall impulse response matrix by combining the mixing system, beamforming, and blind source separation.
, the overall impulse response matrix by combining the mixing system, beamforming, and blind source separation.
4.2. Dereverberation Experiment
The proposed algorithm is used for separating three sources using a 16-element circular microphone array with a radius of 0.2 m. The environment is shown in Figure 6. The simulated room reverberation time is  = 300 ms, where
= 300 ms, where  is the time required for the sound level to decrease by 60 dB. This is a medium reverberant condition. One typical room impulse response is shown in Figure 7(a). Three source locations (2, 4, 6) are used, and the sources are two male speeches and one female speech of 8 seconds each. Three beams are formed by the microphone array pointing at the three sources, respectively. Impulse responses associated with the global transfer function of beamforming is shown in Figure 8, which are calculated from the impulse responses of mixing filters and beamforming filters using
is the time required for the sound level to decrease by 60 dB. This is a medium reverberant condition. One typical room impulse response is shown in Figure 7(a). Three source locations (2, 4, 6) are used, and the sources are two male speeches and one female speech of 8 seconds each. Three beams are formed by the microphone array pointing at the three sources, respectively. Impulse responses associated with the global transfer function of beamforming is shown in Figure 8, which are calculated from the impulse responses of mixing filters and beamforming filters using

It can be seen that the diagonal components in Figure 8 are superior to off-diagonal ones. This implies that the target sources are dominant in the outputs. To demonstrate the dereverberation performance of beamforming, Figure 8(a) is enlarged in Figure 7(b) and compared with the original impulse response in Figure 7(a). Obviously, the mixing filter becomes shorter after beamforming, and the reverberation becomes smaller. This indicates that dereverberation is achieved. So far, the two advantages of beamforming, dereverberation and noise reduction, are observed as expected. Thus the new mixing network  (n) should be easier to separate than the original mixing network. In this experiment, the average input SIR is SIRIN =
(n) should be easier to separate than the original mixing network. In this experiment, the average input SIR is SIRIN =  dB, and the output one, enhanced by beamforming, is SIRBM = 3.3 dB. Setting the STFT frame size at 2048 and applying BSS to the beamformed signals, we get an average output SIR of the combined method of SIROUT = 16.3 dB, a 19.1 dB improvement over the input: 6.1 dB improvement at the beamforming stage, and 13 dB further improvement at the BSS stage.
dB, and the output one, enhanced by beamforming, is SIRBM = 3.3 dB. Setting the STFT frame size at 2048 and applying BSS to the beamformed signals, we get an average output SIR of the combined method of SIROUT = 16.3 dB, a 19.1 dB improvement over the input: 6.1 dB improvement at the beamforming stage, and 13 dB further improvement at the BSS stage.
4.3. Experiments Reverberant Environments
Three experiments are conducted to investigate the performance of the proposed method and compare it with the BSS-only and the beamforming-only method. The first examines the performance of the BSS-only method in medium reverberation with different STFT frame sizes. The second compares the performance of the proposed method and the other two methods in various reverberant conditions. The third examines the performance of the proposed method with various microphone array sizes.
4.3.1. BSS with Different STFT Frame Size
The simulation environment for the BSS-only method shown in Figure 9 is the same as Figure 6 except that the microphone array is replaced by four linearly arranged microphones. The distance between any two adjacent microphones is 6 cm. The reverberation time is  = 300 ms. One
= 300 ms. One  (2 sources and 2 microphones) and one
(2 sources and 2 microphones) and one  (4 sources and 4 microphones) cases were simulated. For the
(4 sources and 4 microphones) cases were simulated. For the  case, microphones B, C, and source locations (2, 6) are used. The sources are one male speech and one female speech of 8 seconds each. For the
case, microphones B, C, and source locations (2, 6) are used. The sources are one male speech and one female speech of 8 seconds each. For the  case, all four microphones and four source locations (1, 2, 4, 6) are used. The sources are two male speeches and two female speeches of 8 seconds each. Blind source separation with different STFT frame size ranging from 512 to 5120 is tested. The output SIR of blind source separation is calculated in a manner similar to the one presented in Section 4.1. The simulation results are shown in Figure 10. The performance in the
case, all four microphones and four source locations (1, 2, 4, 6) are used. The sources are two male speeches and two female speeches of 8 seconds each. Blind source separation with different STFT frame size ranging from 512 to 5120 is tested. The output SIR of blind source separation is calculated in a manner similar to the one presented in Section 4.1. The simulation results are shown in Figure 10. The performance in the  case is always better than that in the
case is always better than that in the  case since it is easier to separate 2 sources than 4 sources. In both
case since it is easier to separate 2 sources than 4 sources. In both  and
and  cases, the separation performance peaks at the STFT frame size of 2048. This verifies the early discussion about the dilemma in determining the STFT frame size: the separation performance is saturated before reaching a sufficient performance level.
cases, the separation performance peaks at the STFT frame size of 2048. This verifies the early discussion about the dilemma in determining the STFT frame size: the separation performance is saturated before reaching a sufficient performance level.
Obviously, an optimal STFT frame size may exist for a specific reverberation. However, due to complex acoustical environments and varieties of source signals, it is difficult to determine this value precisely. How to choose an appropriate frame length may be a topic of our future research. Generally, 1024 or 2048 can be used as a common frame length. Here we use an analysis frame length of 2048 for all reverberant conditions in the remaining experiments.
4.3.2. Performance Comparison among Three Methods
The performances of the combined method, the BSS-only method, and the beamforming-only method are compared in different reverberant environments. The beamforming-only method is equal to the first processing stage of the combined method. The simulation environment of the combined method is shown in Figure 6 and the BSS-only method in Figure 9. For the combined method, a 16-element microphone array with a radius of 0.2 m is used. Various combinations of source locations are tested (2 sources and 4 sources). The sources are two male speeches and two female speeches of 8 seconds each.  ranges from 100 ms to 700 ms in increments of 200 ms. The average input SIR does not vary significantly with the reverberation time: it is about 0 dB for 2 sources, and
ranges from 100 ms to 700 ms in increments of 200 ms. The average input SIR does not vary significantly with the reverberation time: it is about 0 dB for 2 sources, and  dB for 4 sources. For all three methods, the STFT frame size is set at 2048. The separation results are shown in Figure 11, with each panel depicting the output SIRs of the three methods for one source combination. It's observed in Figure 11 that, for each source configurations, the output SIRs of all methods decrease with increasing reverberation; however, the combined method always outperforms the other two. Beamforming performs worst among the three methods, however, it provides a good preprocessing result, and hence the combined method works better than the BSS-only method.
dB for 4 sources. For all three methods, the STFT frame size is set at 2048. The separation results are shown in Figure 11, with each panel depicting the output SIRs of the three methods for one source combination. It's observed in Figure 11 that, for each source configurations, the output SIRs of all methods decrease with increasing reverberation; however, the combined method always outperforms the other two. Beamforming performs worst among the three methods, however, it provides a good preprocessing result, and hence the combined method works better than the BSS-only method.
It is interesting to investigate how big an improvement one can obtain by the use of beamforming preprocessing in different reverberation. To measure the contribution of this preprocessing, we define the relative improvement of the combined method over the BSS-only method as

where

with the subscripts  and
and  standing for the BSS-only method and the combined method, respectively. We calculate the relative performance improvement for the 4 separation scenarios listed in Figure 11 and show the average result in Figure 12. As discussed previously, the performance is improved by the combined method for all reverberant conditions. However, it is also observed in Figure 12 that the improvement in low reverberation is not as large as in medium and high reverberation. That is, the use of beamforming in low reverberation is not as beneficial as it would be for high reverberation. The reason is that, BSS can work well alone when the circular convolution approximation problem is not evident in low reverberation, and thus the contribution of preprocessing is small. On the other hand, when the circular convolution approximation problem become severe in high reverberation, the contribution of preprocessing becomes crucial and hence the separation performance is improved significantly.
standing for the BSS-only method and the combined method, respectively. We calculate the relative performance improvement for the 4 separation scenarios listed in Figure 11 and show the average result in Figure 12. As discussed previously, the performance is improved by the combined method for all reverberant conditions. However, it is also observed in Figure 12 that the improvement in low reverberation is not as large as in medium and high reverberation. That is, the use of beamforming in low reverberation is not as beneficial as it would be for high reverberation. The reason is that, BSS can work well alone when the circular convolution approximation problem is not evident in low reverberation, and thus the contribution of preprocessing is small. On the other hand, when the circular convolution approximation problem become severe in high reverberation, the contribution of preprocessing becomes crucial and hence the separation performance is improved significantly.
The experiments in this part illustrate the superiority of the proposed method over using beamforming or blind source separation alone. The comparison between proposed method with other hybrid methods in different reverberant conditions will be further investigated in our future research.
4.3.3. Performance of the Combined Method with Different Microphone Array Size
Since the performance of a beamformer is significantly affected by the array size, it is reasonable to ask how much the array size will impact the performance of the proposed method. Some experiments are carried out on this topic. The simulation environment is shown in Figure 6. Three microphone arrays are used to design the beamformer: an 8-element array with a radius of 0.1 m, a 16-element array with a radius of 0.2 m, and a 24-element array with a radius of 0.2 m. Various combinations of source locations are tested (2 sources and 4 sources). The sources are two male speeches and two female speeches of 8 seconds each. The STFT frame size is set at 2048. The performance of the proposed combined method under  of 300 ms (medium reverberation) and 700 ms (high reverberation) is shown in Figures 13 and 14, respectively. It can be seen that, for all source configurations, the separation performance improves with increasing array size. For example, in the two bottom panels of Figure 14, the output SIR with an 8-element array is only about 2 dB, but rises to about 6 dB with a 24-element array. A higher output SIR can be anticipated for larger array sizes. However, the better performance is obtained at the cost of high computation and more hardware associated with more microphones. Thus, a tradeoff should be considered in actual applications.
of 300 ms (medium reverberation) and 700 ms (high reverberation) is shown in Figures 13 and 14, respectively. It can be seen that, for all source configurations, the separation performance improves with increasing array size. For example, in the two bottom panels of Figure 14, the output SIR with an 8-element array is only about 2 dB, but rises to about 6 dB with a 24-element array. A higher output SIR can be anticipated for larger array sizes. However, the better performance is obtained at the cost of high computation and more hardware associated with more microphones. Thus, a tradeoff should be considered in actual applications.
5. Conclusion
Given the poor performance of blind source separation in high reverberation, the paper proposes a method which combines beamforming and blind source separation. Using superdirective beamforming as a preprocessor of frequency-domain blind source separation, the combined method is able to integrates the advantages of both techniques and complements the weakness of them alone. Simulation in different conditions ( = 100 ms–700 ms) illustrates the superiority of the proposed method over using beamforming or blind source separation alone; and the performance improvement increases with the microphone array size. The proposed method is promising for real-time processing with its high computational efficiency.
= 100 ms–700 ms) illustrates the superiority of the proposed method over using beamforming or blind source separation alone; and the performance improvement increases with the microphone array size. The proposed method is promising for real-time processing with its high computational efficiency.
References
Van Veen BD, Buckley KM: Beamforming: a versatile approach to spatial filtering. IEEE ASSP magazine 1988, 5(2):4-24.
Van Trees HL: Optimum Array Processing—Part IV of Detection, Estimation, and Modulation Theory. Wiley-Interscience, New York, NY, USA; 2002.
Hyvarien A, Karhunen J, Oja E: Independent Component Analysis. John Wiley & Sons, New York, NY, USA; 2001.
Pedersen MS, Larsen J, Kjems U, Parra LC: A survey of convolutive blind source separation methods. In Springer handbook on Speech Processing and Speech Communication. Springer, London, UK; 2007:1-34.
Douglas SC, Sun X: Convolutive blind separation of speech mixtures using the natural gradient. Speech Communication 2003, 39(1-2):65-78. 10.1016/S0167-6393(02)00059-6
Aichner R, Buchner H, Yan F, Kellermann W: A real-time blind source separation scheme and its application to reverberant and noisy acoustic environments. Signal Processing 2006, 86(6):1260-1277. 10.1016/j.sigpro.2005.06.022
Douglas SC, Gupta M, Sawada H, Makino S: Spatio-temporal FastICA algorithms for the blind separation of convolutive mixtures. IEEE Transactions on Audio, Speech and Language Processing 2007, 15(5):1511-1520.
Smaragdis P: Blind separation of convolved mixtures in the frequency domain. Neurocomputing 1998, 22(1–3):21-34.
Sawada H, Araki S, Makino S: Frequency-domain blind source separation. In Blind Speech Separation. Springer, London, UK; 2007:47-78.
Murata N, Ikeda S, Ziehe A: An approach to blind source separation based on temporal structure of speech signals. Neurocomputing 2001, 41(1–4):1-24.
Sawada H, Araki S, Makino S: Measuring dependence of bin-wise separated signals for permutation alignment in frequency-domain BSS. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '07), May 2007 3247-3250.
Saruwatari H, Kurita S, Takeda K, Itakura F, Nishikawa T, Shikano K: Blind source separation combining independent component analysis and beamforming. EURASIP Journal on Applied Signal Processing 2003, 2003(11):1135-1146. 10.1155/S1110865703305104
Ikram MZ, Morgan DR: Permutation inconsistency in blind speech separation: Investigation and solutions. IEEE Transactions on Speech and Audio Processing 2005, 13(1):1-13.
Sawada H, Mukai R, Araki S, Makino S: A robust and precise method for solving the permutation problem of frequency-domain blind source separation. IEEE Transactions on Speech and Audio Processing 2004, 12(5):530-538. 10.1109/TSA.2004.832994
Araki S, Mukai R, Makino S, Nishikawa T, Saruwatari H: The fundamental limitation of frequency domain blind source separation for convolutive mixtures of speech. IEEE Transactions on Speech and Audio Processing 2003, 11(2):109-116. 10.1109/TSA.2003.809193
Hiroe A: Blind vector deconvolution: convolutive mixture models in short-time Fourier transform domain. Proceedings of the International Workshop on Independent Component Analysis (ICA '07), 2007, Lecture Notes in Computer Science 4666: 471-479.
Nishikawa T, Saruwatari H, Shikano K: Blind source separation of acoustic signals based on multistage ICA combining frequency-domain ICA and time-domain ICA. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 2003, E86-A(4):846-858.
Silverman HF, Yu Y, Sachar JM, Patterson WR III: Performance of real-time source-location estimators for a large-aperture microphone array. IEEE Transactions on Speech and Audio Processing 2005, 13(4):593-606.
Madhu N, Martin R: A scalable framework for multiple speaker localisation and tracking. Proceedings of the InternationalWorkshop on Acoustic Echo and Noise Control, 2008, Seatle, Wash, USA 1-4.
Parra L, Fancourt C: An adaptive beamforming perspective on convolutive blind source separation. In Noise Reductionin Speech Applications. Edited by: Davis GM. CRC Press, Boca Raton, Fla, USA; 2002:361-376.
Ikram MZ, Morgan DR: A beamforming approach to permutation alignment for multichannel frequency-domain blind speech separation. Proceedings of the IEEE International Conference on Acustics, Speech, and Signal Processing, May 2002 1: 881-884.
Parra LC, Alvino CV: Geometric source separation: Merging convolutive source separation with geometric beamforming. IEEE Transactions on Speech and Audio Processing 2002, 10(6):352-362. 10.1109/TSA.2002.803443
Saruwatari H, Kawamura T, Nishikawa T, Lee A, Shikano K: Blind source separation based on a fast-convergence algorithm combining ICA and beamforming. IEEE Transactions on Audio, Speech and Language Processing 2006, 14(2):666-678.
Gupta M, Douglas SC: Beamforming initialization and data prewhitening in natural gradient convolutive blind sourceseparation of speech mixtures. In Independent Component Analysis and Signal Separation. Volume 4666. Springer, Berlin, Germany; 2007:512-519. 10.1007/978-3-540-74494-8_64
Bingham E, Hyvärinen A: A fast fixed-point algorithm for independent component analysis of complex valued signals. International Journal of Neural Systems 2000, 10(1):1-8.
Bell AJ, Sejnowski TJ: An information-maximization approach to blind separation and blind deconvolution. Neural Computation 1995, 7(6):1129-1159. 10.1162/neco.1995.7.6.1129
Amari S, Cichocki A, Yang HH: A new learning algorithm for blind signal separation. Advances in Neural Information Processing Systems 1996, 8: 757-763.
Pan Q, Aboulnasr T: Combined spatial/beamforming and time/frequency processing for blind source separation. Proceedings of the European Signal Processing Conference, 2005, Antalya, Turkey 1-4.
Cox H, Zeskind RM, Kooij T: Practical supergain. IEEE Transactions on Acoustics, Speech, and Signal Processing 1986, 34(3):393-398. 10.1109/TASSP.1986.1164847
Ryan JG, Goubrân RA: Array optimization applied in the near field of a microphone array. IEEE Transactions on Speech and Audio Processing 2000, 8(2):173-176. 10.1109/89.824702
Bouchard C, Havelock DI, Bouchard M: Beamforming with microphone arrays for directional sources. Journal of the Acoustical Society of America 2009, 125(4):2098-2104. 10.1121/1.3089221
Douglas SC, Gupta M: Scaled natural gradient algorithms for instantaneous and convolutive blind source separation. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '07), April 2007 2: 637-640.
Wang L, Ding H, Yin F: A region-growing permutation alignment approach in frequency-domain blind source separationof speech mixtures. IEEE Transactions on Audio, Speech and Language Processing. In press
Matsuoka K, Nakashima S: Minimal distortion principle for blind source separation. Proceedings of the International Workshop on Independent Component Analysis (ICA '01), 2001 722-727.
Allen JB, Berkley DA: Image method for efficiently simulating small-room acoustics. Journal of the Acoustical Society of America 1979, 65(4):943-950. 10.1121/1.382599
Acknowledgments
This paper is partly supported by the National Natural Science Foundation of China (60772161, 60372082) and the Specialized Research Fund for the Doctoral Program of Higher Education of China (200801410015). This paper is also supported by NRC-MOE Research and Post-doctoral Fellowship Program from Ministry of Education of China and National Research Council of Canada. The authors would like to thank Dr. Michael R. Stinson of National Research Council Canada for his invaluable discussions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, L., Ding, H. & Yin, F. Combining Superdirective Beamforming and Frequency-Domain Blind Source Separation for Highly Reverberant Signals. J AUDIO SPEECH MUSIC PROC. 2010, 797962 (2010). https://doi.org/10.1155/2010/797962
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/797962

 samples of the impulse response
samples of the impulse response 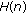 , not its entirety.
, not its entirety.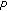 is short compared to
is short compared to 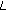 .
.











