- Research
- Open access
- Published:
A memory efficient finite-state source coding algorithm for audio MDCT coefficients
EURASIP Journal on Audio, Speech, and Music Processing volume 2014, Article number: 22 (2014)
Abstract
Abstract
To achieve a better trade-off between the vector dimension and the memory requirements of a vector quantizer (VQ), an entropy-constrained VQ (ECVQ) scheme with finite memory, called finite-state ECVQ (FS-ECVQ), is presented in this paper. The scheme consists of a finite-state VQ (FSVQ) and multiple component ECVQs. By utilizing the FSVQ, the inter-frame dependencies within source sequence can be effectively exploited and no side information needs to be transmitted. By employing the ECVQs, the total memory requirements of the FS-ECVQ can be efficiently decreased while the coding performance is improved. An FS-ECVQ, designed for the modified discrete cosine transform (MDCT) coefficients coding, was implemented and evaluated based on the Unified Speech and Audio Coding (USAC) scheme. Results showed that the FS-ECVQ achieved a reduction of the total memory requirements by about 11.3%, compared with the encoder in USAC final version (FINAL), while maintaining a similar coding performance.
1 Introduction
It is well known that a memoryless vector quantizer (VQ) can achieve performance arbitrarily close to the rate-distortion (R/D) function of the source, if the codevector dimension is large enough [1]. However, with the increase of the codevector dimension, the memory requirements and the computational complexity of the VQ will also increase exponentially. Furthermore, it will be difficult to design a practical VQ with high performance in a high-dimensional space. Consequently, various product codevector quantization methods [2–5] have been proposed as alternative solutions. These methods cut down the memory requirements and reduce the computational complexity with a moderate loss of quantization performance. Among the widely reported product code techniques, split vector quantizer (SVQ), which was first proposed by Paliwal and Atal [6] for linear predictive coding (LPC) parameters quantization, receives extensive attention. In a SVQ, the input vector is first split into multiple subvectors [7], and then the resulting subvectors are quantized independently [8, 9]. Although the SVQ cuts down the memory requirements and reduces the computational complexity of a memoryless VQ, it ignores the correlations between the subvectors and, hence, leads to a coding loss, referred to as ‘split loss’ [10].
In order to recover the split loss, many techniques have been developed. So and Paliwal [2, 11] have proposed a switched SVQ (SSVQ) method, which adds multiple different SVQs to the input vector space so as to exploit the global dependencies. Based on SSVQ, a Gaussian mixture model (GMM)-based SSVQ (GMM-SSVQ) was proposed by Chatterjee et al. [12], where the distribution of the source is modeled by a GMM. Furthermore, a GMM-based Karhunen-Loève transform (KLT) domain SSVQ was proposed by Lee et al. [13], which was constructed by adding a region-clustering algorithm to the GMM-SSVQ. To better exploit the probability density function (pdf) of the source, Chatterjee and Sreenivas [14] developed a switched conditional pdf-based SVQ where the vector space is partitioned into non-overlapping Voronoi regions, and the source pdf of each switching Voronoi region is modeled by a multivariate Gaussian. Although these methods efficiently recover the split loss, most of them simply focus on removing intra-frame redundancies and fail to exploit inter-frame redundancies.
In addition, ordinary VQs can generally be divided into two groups: entropy-constrained VQ (ECVQ) [15] and resolution-constrained VQ (RCVQ) [16], and the above-mentioned methods are mainly proposed for the RCVQ and can hardly be applied on the ECVQ [17]. In the other side, an ECVQ usually achieves better R/D performance than a RCVQ does [18]. This is mainly owing to the length function contained in the ECVQ which allocates a different number of bits to different vector indices according to the probability of their appearance. Therefore, an ECVQ with recovered split loss would achieve a higher R/D performance than a RCVQ does.
To better recover the split loss of a SVQ, the finite-state VQ (FSVQ) can usually be resorted to, which is able to efficiently take advantage of the inter-frame dependencies. FSVQ [19, 20], which incorporates memory into a memoryless VQ, is intrinsically a prediction-based technique. An FSVQ can be regarded as a finite-state machine [21], which contains multiple states, each corresponding to a certain state codebook. The state transition is determined by a next-state function based on the information obtained from the previously encoded vectors. Thus, the FSVQ utilizes the previous encoded vectors to predict the current input [22] and, therefore, efficiently exploits the redundancies among the input vectors and achieves a considerable increase in the R/D performance over a memoryless VQ.
In this paper, a composite quantizer, called FS-ECVQ, is introduced, in which multiple ECVQs are combined with a FSVQ. In FS-ECVQ [23], this FSVQ serves as a classifier which splits the source sequence into multiple clusters. To achieve better classification performance, the FSVQ draws the current decision based on information obtained from a number of previous adjacent vectors, even from those in previous frames, and thus better exploits the inter-frame redundancies than an ordinary SVQ does. After that, a specially designed ECVQ is applied on each cluster derived from the FSVQ. Among the resulting clusters, the more frequently a cluster occurred, the higher vector dimension it will be assigned. Through this method, the total memory requirements can be significantly reduced and the coding performance can be obviously improved. Moreover, within each component ECVQ, multiple length functions are devised for coding the indices of input vectors, each corresponding to a certain pdf model. To select the optimal length function for each vector index, another FSVQ is introduced. This FSVQ predicts the source pdf of the current vector index based on the information obtained from its previous adjacent ones, and then the length function with the highest matching probability is chosen. Through this method, the ‘mismatch’ between the designed pdf and the source pdf can be efficiently decreased. Thus, the FS-ECVQ will be more robust than an ordinary SVQ.
The organization of this paper is as follows. In Section 2, some fundamentals about VQ, FSVQ, and ECVQ are introduced. Section 3 deals with the design of the FS-ECVQ. Then, in Section 4, a practical FS-ECVQ aimed at coding the audio-modified discrete cosine transform (MDCT) coefficients in the MPEG Unified Speech and Audio Coding (USAC) [24] is implemented and tested. Finally, conclusions are presented in Section 5.
2 Preliminaries
Since FS-ECVQ is based on FSVQ and ECVQ, in this section we will review the classical results of these vector quantization theories under the high rate assumption.
2.1 Vector quantization
Generally, a VQ, q, consists of four elements: encoder ϕ, decoder ψ, index coder ζ, and codebook  . Suppose that random vector, x, with pdf, f, is quantized by quantizer q and the corresponding reconstructed vector is . Then, for a given measurable space consisting of a k-dimensional Euclidean space Ω and its Borel subset, the mappings of quantizer q can be described as follows:
. Suppose that random vector, x, with pdf, f, is quantized by quantizer q and the corresponding reconstructed vector is . Then, for a given measurable space consisting of a k-dimensional Euclidean space Ω and its Borel subset, the mappings of quantizer q can be described as follows:
-
Encoder ϕ: , where
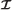 is a countable index set. Each element in
is a countable index set. Each element in 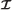 corresponds to a different codevector contained in codebook
corresponds to a different codevector contained in codebook 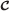 . The aim of encoder ϕ is to find the index of the best matching vector in codebook
. The aim of encoder ϕ is to find the index of the best matching vector in codebook 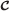 for input vector x according to a given distortion criterion
for input vector x according to a given distortion criterion -
Decoder ψ: , which is used to reconstruct the vector in space Ω according to the received vector index
-
Index coder ζ: , which transforms the index sequence generated from encoder ϕ to a bitstream
-
Codebook
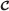 , which is used by both encoder ϕ and decoder ψ to generate the optimal codevector indices or to find the corresponding codevectors
, which is used by both encoder ϕ and decoder ψ to generate the optimal codevector indices or to find the corresponding codevectors
The average rate and the entropy of quantizer q are
respectively, where p i denotes the occurrence probability of index i. According to the result in [25], it implies that
with equality if and only if ζ(i)=− lnp i . Therefore, the optimal length function of quantizer q for pdf f is
The performance of quantizer q can be measured by an average distortion
In our work, Euclidean distance, , is used as the distortion measure, where ∥·∥ denotes the l2 norm.
2.2 Finite-state vector quantization
FSVQ is a VQ with a time-varying encoder and decoder pair [21], which is realized by means of a finite-state machine. Assume that a FSVQ contains M distinct states, S1,…,S M , whose corresponding state codebooks are, , respectively. Suppose that x n is the input vector, whose current state is s n ∈{S1,…,S M }. Then, by searching the codebook , corresponding to the current state s n , for the best matching codevector , the input vector x n can be quantized, whose vector index is denoted as i n .
In FSVQ, the current state s n is achieved using a next-state function [26], γ, which can be written as
where in−1 and sn−1 are the index and state of the last vector xn−1, respectively. Thus, the state transition is determined by the next-state function, and the current state s n can be considered as a prediction to the input vector x n based on the previously encoded vectors. Once the current state s n is obtained, the encoding procedure of the FSVQ [20] can be written as
which implies that the input vector x n is quantized in the codebook corresponding to the current state s n .
Similarly, the decoding procedure of the FSVQ is also based on the current state s n . In this procedure, the received vector index i n and its current state s n are combined to reconstruct the input vector x n . The decoding procedure can be shown as
which implies that the received vector index, i n , is decoded in the codebook corresponding to the current state s n .
In FSVQ, encoder ϕ and decoder ψ are synchronized using the following coding rule:
2.3 Entropy-constrained vector quantization
The design of an ECVQ is to find a set of reconstruction vectors which minimizes the average distortion between the source and its reconstruction, subject to a constraint on the index entropy [15]. To obtain a common conclusion, Gray et al. [25, 27] investigated the variable-rate ECVQ using a Lagrangian formulation in which a Lagrangian multiplier λ>0 is defined for each rate.
Assume that the pdf, f, of random vector x is absolutely continuous with respect to Lebesgue measure, that exists and is finite and that H f (q1)<∞, where q1 is a cubic lattice quantizer with unit volume cells, the Lagrangian distortion of ECVQ, q, can be given by
and the optimal performance can be written as
where D f (q) and R f (q), obtained from (5) and (1), are the average rate and average distortion of quantizer q, respectively.
In order to demonstrate the variable-rate results of the research done by Gray et al. in a simplified form, we introduce the following notations:
where ξ k is a finite constant and μ1 is the uniform pdf on the k-dimensional unit cube C1= [0,1)k. Then, the main result of the researches done by Gray et al. [25] is the following:
This result guarantees that if a pdf f satisfies the conditions of (15), then there exists an optimal quantizer q for f in the sense that for any decreasing λ converging to 0, its optimal performance is ξ k .
Mismatch appears if there exists any difference between the designed pdf and the source pdf. Suppose that the designed pdf is g and the source pdf is f, then according to the mismatch theorem proposed in [28], the minimal distortion of quantizer q can be given as
where I(f||g) is the relative entropy and can be given as
Compared with (15), it can be seen that the mismatch resulted from applying an asymptotically optimal quantizer for pdf g to a source sequence with pdf f is exactly the relative entropy of the source pdf f to the design pdf g, I(f||g).
3 Quantizer design
Compared with a conventional ECVQ, such as the quantization methods of USAC, whose architecture is to be described in details in Section 4, the FS-ECVQ can be taken as a super-ECVQ, in which multiple component ECVQs are contained and all of them are combined to a FSVQ. Thus, the FS-ECVQ is composed of two steps. The first step is to split the source sequence into multiple clusters using the FSVQ (main FSVQ), and the second step is to apply a dedicated conventional ECVQ to each cluster. Suppose that the largest available vector dimension is 8, the whole coding scheme of a FS-ECVQ can be demonstrated as Figure 1.
3.1 Main FSVQ
The major function of the main FSVQ is to partition the input space into four non-overlapped clusters according to the four states contained. For each resulting cluster, a component ECVQ is constructed holding a different vector dimension and different memory requirements. By this means, the total memory requirements could be efficiently decreased. The state transition is determined by a next-state function, which is the key component of the main FSVQ. In the following part of this section, we will mainly discuss the construction of the next-state function.
The next-state function of the main FSVQ is built on the dependencies among audio MDCT coefficients. In practice, audio signals are usually divided into a series of time intervals (often referred to as ‘frames’) due to their long-term time-varying property, and over a specified frame they are assumed to be stationary. Thus, as an expression of the audio signal in MDCT domain, there are high dependencies among the MDCT coefficients of the adjacent frames as well as among the coefficients within one frame. As a result, based on the inter- and intra-frame correlations, the MDCT coefficients of current frame could be estimated through prediction methodology. In our work, the audio MDCT coefficient frames are further divided into small blocks, and then, by estimating the shape properties of these blocks among multiple sequential frames, the next-state function is constructed in order to exploit both the intra- and inter-frame dependencies. In fact, within an audio MDCT coefficient sequence, the occurrence frequency of a block is highly related to its shape features. Suppose the block size is 4, then the relationship of the shape feature and the occurrence of a block are demonstrated in Figure 2.
To characterize the shape of a block, three statistical parameters block energy, e, block deviation, σ, and block skewness, g, are employed in our work. Let μ be the mean value of block x. Then the parameters e, σ, and g can be written as
where x i and N are the i th element and the length of block x, respectively. To describe the shape feature of block x in a simplified form, a new statistical parameter, V x , is defined, which is given as
Once a source sequence is split into a series of blocks, the value of V x will be calculated for each block. Thus, a mapping can be established between the V x set, composed of all the possible values of V x , and the input space Ω. Then, by splitting the possible values of V x into two segments, we can partition the input space Ω into two clusters, Ω k and . Here, k denotes the dimension of cluster Ω k . To implement the split, a threshold VT is employed, whose value is obtained by maximizing the coding gain of the FS-ECVQ under the constraint of the total memory requirements using the training data. As for the two resulting clusters, Ω k is supposed to contain the blocks occurring relatively frequently, whereas is assumed to hold those occurring relatively scarcely.
To construct the next-state function, four previous blocks, A, B, C, and D, which are adjacent to the current block, x, can be employed [29]. For simplicity, we assume that the current block and its previous neighbors form a Markov chain [26]. The relative positions of all these blocks are demonstrated in Figure 3. Assume that the shape parameters of the four adjacent blocks are independent measurements, then according to the research done by Nasrabadi et al. [30], the conditional joint posterior probability, which the next-state function is built on, can be given as
where V x and V i are the shape parameters of block x and its four neighbors A, B, C, and D, respectively. Suppose that P(V x ) and P(V i ) are measured independently and considered to be equal, then probability P(V i |V x ) will be equal to probability P(V x |V i ), which represents a conditional probability of the parameter V x given one of its neighbors V i , for i=A, B, C, and D, and can be obtained through recording all the possible cluster pairs occurring together using the training data. Assume that all the shape parameters obey the same probability distribution, then the conditional joint probability, P(V x |(V A ,V B ,V C ,V D )), will only depend on the four conditional probabilities P(V x |V i ), for i=A, B, C, and D, and the other parameters in (22) will be constant for any input block. Therefore, we can build the next-state function (6) on these four conditional probabilities, and the current state of the main FSVQ, s, can be given by
which denotes an estimation of the cluster to which the current block is most likely to be classified.
To split the source sequence into smaller clusters, a pyramidal decomposing algorithm is employed, as demonstrated in Figure 4. In this algorithm, a block, x, is first separated from the source sequence, whose length is set to be the largest available vector dimension, supposed to be 8. Then, the current state s of the obtained block x, which is calculated through (23), is compared with a given threshold, T8. If current state s is lower than T8, block x will be taken as an element belonging to cluster Ω8. Else, it would be equally decomposed into two smaller blocks, and , whose vector dimensions are both 4, and then the block will be taken as the new current block. Once again, the current state s is calculated and is compared with another threshold, T4. If the obtained state s is lower than T4, the block will be taken as an element belonging to cluster Ω4. Else, it will be decomposed once more. This procedure continues iteratively until the lowest available vector dimension, supposed to be 1, is reached. Since each threshold can be regarded as the occurrence frequency of a block, then the current blocks considered to be with low-occurrence frequency, will be split iteratively, until a suitable vector dimension is found. The whole procedure is summarized in Algorithm 1.

At beginning, there is no previous block, and therefore, an original state, s0, ought to be initialized by the main FSVQ.
3.2 ECVQ
Based on the research done by Gray et al. [25], in our work, Z n lattice quantizer and arithmetic coder are selected as the lattice quantizer and the length function of each component ECVQ, respectively. Unlike conventional ECVQ [15, 17], where all the vector indices generated from the lattice quantizer share a same length function regardless of their possible differences, in our work multiple length functions are available and the optimal one is selected by another FSVQ (sub-FSVQ) for each generated vector index. Moreover, to improve the robustness and, at the same time, decrease the memory requirements of each component ECVQ, the design of sub-FSVQ is optimized and an iterative method to merge the similar length functions is proposed.
The length functions are implemented by an arithmetic coder, which are based on the pdf model of the input index. Hence, the main work of the sub-FSVQ is to search for the optimal one among a predesigned collection of pdf models based on the information obtained from previous indices.
3.2.1 Lattice quantizer
The issue whether an optimal ECVQ has a finite or infinite number of codevectors has been in-depth investigated by Gyärgy and Linder [31]. They found that ECVQ has a finite number of codevectors only if the tail of the source distribution is lighter than the tail of a Gaussian distribution. With respect to the probability distribution of an audio MDCT coefficient sequence, Yu et al. [32] show that the generalized Gaussian function with distribution parameter r=0.5 provides a good approximation. Moreover, in practice, the possible values of the audio MDCT coefficients are always finite and concentrated in a finite range. Therefore, in our work, all codevectors of the lattice quantizer are simply constrained in the range
where X denotes an input vector, and t0 and p0 are two thresholds that constrain the norm and the probability of input vector X, respectively.
Since all the codevectors are constructed within the range (24), the input vectors outside the range will suffer a larger quantization loss than those inside the range. Such circumstances are usually required to be avoided for audio MDCT coefficients quantization. To keep the possible quantization error constant, the input vector which falls outside the range (24) will be split into two parts, the least significant bits (LSB) and the most significant bits (MSB), and then the two parts are encoded separately. Let x=(x1,…,x k ) be a candidate vector, whose vector dimension is k. Assume that after each split the generated MSB and LSB are denoted by x∗ and , respectively, where i denotes the i-th split. To indicate an overflow happens, a symbol, e s c a p e s y m b o l, is employed. The whole procedure is demonstrated in Algorithm 2.

3.2.2 Sub-FSVQ
This FSVQ is used to search for the optimum in a predesigned collection of length functions, which are used to encode the current vector index generated from the lattice quantizer. The next-state function of the sub-FSVQ, , is built on the four previous indexes I A , I B , I C , and I D , adjacent to the current input, I x . Since the ECVQ holds a finite number of codevectors, the simplest way to construct the next-state function is to enumerate all the possible combinations of the four neighbors, each denoting a certain state. But with the increase of the number of codevectors, the possible number of current states will be extremely large, and thus, the memory requirements and the computation cost skyrocket.
To reduce the number of possible current states, the different dependencies between the current index and its four previous neighbors must be taken into account. In practice, less emphasis is placed on indices I A and I C than on indices I B and I D . This is due to the fact that among the four neighbors, current vector x is less relevant to vectors A and C than to vectors B and D. Thus, we apply the operation ||·||2 to vectors A and C, so as to reduce the number of their possible values.
The location of the current vector should also be considered. The frame, current vector located, can be generally classified into two types: the normal frame and the reset frame. In addition, within a frame the current vector can be located at the normal position or the starting position. Thus, there exist four cases, as demonstrated in Figure 5. Specially, if the current vector is located at the starting position of a reset frame, there will be no adjacent vector to build the next-state function, then a special state, , should be assigned.
As a result, the next-state function of the sub-FSVQ can be written as
where i denotes that the sub-FSVQ belongs to the i-th ECVQ and t0, t1, and t2 are three constants making each combination of the four indices corresponding to a different current state. This is feasible since for an audio MDCT coefficient sequence, the values of the four variables, I B , I D , , and , are all finite, and then according to their maximum possible values, it is easy to find the possible values of the three constants.
3.2.3 Length function
The length functions are realized by an arithmetic coder holding multiple pdf models. There are two difficulties in building an optimal arithmetic coder for an optimal ECVQ. First, the memory requirements for saving the predesigned pdf models will become infeasible as the number of states derived from (25) increases. Second, as the volumes of the partitions split by the sub-FSVQ shrink, the available data may not provide credible pdf estimation. Popat and Picard [33] proposed a solution to the second problem using a Gaussian mixture model (GMM) for describing the source pdf. Thus, this work mainly focuses on reducing the memory requirements for saving the pdf models necessary for the arithmetic coder.
The memory requirements can be reduced by merging the similar pdf models. However, according to (16), if one pdf model is replaced by another, mismatch will inevitably take place. Let g be the true pdf of the input signal and suppose that Ω g is its support. Assume that , whose corresponding pdf model is for , is a finite partition of Ω g and that P g (S m )≤0 for all m. Assume also that model g m is replaced by another model, g n , then according to (17) the mismatch of the pdf model pair, g m and g n , denoted by dmis(m,n), can be given as
where ρ m , which equals to the probability P g (S m ), is the weight of model g m . Thus, the mismatch dmis can be seen as a distance measure of a pdf model pair. The more similar the two models are, the smaller is the mismatch. Therefore, we can efficiently decrease the memory requirements for saving the pdf models by merging the model pairs, which hold small enough mismatches, into a new pdf model with a negligible loss of the coding performance.
For a pdf model collection, once we have obtained the dmis values of each model pair, we can merge the ones with minimal dmis values into a new pdf model so as to reduce the memory requirements. If the memory size is still above the requirements, the mergence of the similar pdf models should be continued. But once a new pdf model is generated, the mismatches among pdf models should be updated first. And then, a new merge can be executed. The whole procedure will be carried out iteratively, until the memory size reaches the requirements. Once the final pdf models are obtained, a remapping between these models and their corresponding states is needed.
4 Results
In USAC [34], an up-to-date MPEG standardization, MDCT plays an important role [35]. In the USAC encoder, the MDCT coefficients are firstly companded with a power low function before scalar quantization, achieving in effect a non-uniform scalar quantization. And then, the residuals are further entropy coded. To improve the performance of MDCT coefficients quantization and coding, a novel scheme [29], which combined a scalar quantization with a context-based entropy coding, was developed in the USAC. In this new scheme, the input tuples (blocks) were first quantized by a scalar quantizer (SQ), and then the generated tuple indices were further encoded through a context-based arithmetic encoder. In the USAC final version (FINAL), the tuple length of this scheme was selected to be 2, in order to decrease the total memory requirements.
To further reduce the memory requirements and improve the R/D performance of the MDCT coefficients quantization and coding, a FS-ECVQ was implemented and tested based on the USAC final version. The implemented FS-ECVQ consisted of three component ECVQs, ECVQ_CB4, ECVQ_CB2, and ECVQ_CB1, of which the vector dimensions were 4, 2, and 1, respectively.
To make an easy comparison with the FINAL, the FS-ECVQ was divided into two parts, SQ, which was formed by merging the scaling steps contained in the three component ECVQs and constructed just the same as the one in the FINAL, and the core module of FS-ECVQ, which was referred to FS-ECVQ for simplicity. Thus, the FS-ECVQ and the FINAL would share the same source sequence and the same quantization error and only differ in their coding performance. Therefore, the remainder of this section was mainly focused on evaluating the coding performance of the FINAL and the FS-ECVQ.
4.1 Memory requirements
The total memory requirements of the FINAL and the FS-ECVQ were demonstrated in Table 1. From Table 2, it could be seen that the number of codevectors in FS-ECVQ and FINAL were 85 and 17, respectively. This implied that the equivalent vector dimension of FS-ECVQ would be slightly higher than 2, the dimension of FINAL. Generally, fewer codevectors would lead to a smaller number of vector indices and a smaller memory requirements of each cumulative distribution function (cdf) model. Thus, compared with the FINAL, the FS-ECVQ held a much higher memory requirements for preserving the cdf models.
Compared with FINAL, the FS-ECVQ was less memory exhausting in cdf model decision. This was mainly due to the two FSVQs (main FSVQ and sub-FSVQ), which adaptively reshaped the input blocks and merged the states with similar cdf models to be a new one, while at the same time no side information was needed to be transmitted. Thus, the number of states needed to be conserved contained in sub-FSVQ would be much fewer than those contained in the context-model of the FINAL. As a result, the FS-ECVQ further reduced the total memory requirements of the FINAL by up to 11.3%.
The number of codevectors (codebook size) and the memory requirements for saving the cdf models of FINAL and FS-ECVQ were demonstrated in Table 2. It could be seen that the FS-ECVQ employed three different codebooks, whose dimensions were 4, 2, and 1, respectively. Among these codebooks, the 4-dimensional codebook was assigned the largest number of codevectors, whereas the 1-dimensional one was assigned the least. Through this means, the equivalent vector dimension of the FS-ECVQ would be reduced, and therefore, its memory requirements would be efficiently decreased.
4.2 Average computational complexity
The average computational complexities of the FINAL and the FS-ECVQ, whose units were the weighted million operations per second (WMOPS), were shown in Table 3. From this table, it could be seen that the FS-ECVQ and FINAL held a similar average complexity. The average complexity of FS-ECVQ was mainly due to its main FSVQ. In FS-ECVQ, the main FSVQ was used to estimate which cluster the current block would be classified into according to the shape parameters of its four previous adjacent blocks. To obtain these shape parameters, cubic terms were introduced which obviously increased the total computational complexity.
As the cubic terms usually led to a large computation, to reduce the computational complexity, a look-up table was employed in the FS-ECVQ so that the FS-ECVQ held a similar computational complexity as the FINAL. In practice, the size of the look-up table was dependent on the selection of the threshold of the main FSVQ. In our work, to calculate the threshold of current block, four previous neighbors were employed. Since the current block and its four neighbors were highly correlated and usually hold a similar envelope shape, the largest element of all the codevectors could be constrained to a small value, such as 8. Thus, the size of the look-up table for storing the cubic terms would be very small, about two words.
4.3 Rate performance
Nine audio items, covering speech, music, and mixed speech/music signals, were used for the training of the main-FSVQ, sub-FSVQ, and cdf models, of which the bitrates ranged from 12 to 64 kbps, and the length of every item was about 2 h. And among them, four were mono while the others were stereo items. Another nine audio items, also covering speech, music, and mixed speech/music signals, were chosen as the testing set for the FINAL and the FS-ECVQ, of which the bitrates ranged from 12 to 64 kbps and the length of every item was about 3 min. Among them, four were mono while the others were stereo. The testing results were shown in Table 4, where the percentage column represented the increment of the coding gain of the current method over the FINAL.
The table demonstrated that the FINAL and the FS-ECVQ achieved a similar coding performance in all the nine items. This denoted that the FINAL and the FS-ECVQ both could efficiently remove the redundancies within audio MDCT coefficient sequences. Moreover, both FINAL and FS-ECVQ obtained more coding gains in the low bitrate items than in the high bitrate items. These phenomena were mainly due to the fact that the nine items have different pdf of MDCT coefficients. In FS-ECVQ, a different source distribution would lead to a different calling ratio of its three component ECVQs.
4.4 Main FSVQ
The main FSVQ split the input vectors into subvectors according to a pyramidal decomposing method, by which the MDCT coefficient sequence was partitioned into three clusters, Ω4, Ω2, and Ω1. The component ECVQs applied on these resulting clusters were ECVQ_D4, ECVQ_D2, and ECVQ_D1, respectively. To decompose an input vector, in cluster Ω4 and Ω2, the main FSVQ would first calculate two shape parameters from the two pairs of previous adjacent blocks B, D and A, C, respectively, via their corresponding block energies and block skewness, and then, compare them with the two thresholds, T b d and T a c , respectively. Thus, a different combination of the thresholds would lead to a different distribution of the MDCT coefficients among the three component ECVQs, and consequently a different coding gain of the FS-ECVQ. The different combinations of T b d and T a c in the two clusters and their corresponding results were all demonstrated in Table 5. From the table, at least two points could be derived.
First, the thresholds of cluster Ω4 had a larger impact on the coding gain than cluster Ω2 did, which could be explained by the fact that the variation range of the coding gains on Ω4 was much wider than that on Ω2. Furthermore, within a level threshold T b d had a larger impact on the coding gain than threshold T a c did. Since T b d and T a c were obtained from adjacent blocks B, D and A, C, respectively, this proved the assumption that B, D were more significant than A, C.
Second, the component ECVQ, ECVQ_D4, gains than the two others. From Table 5, it could be observed that most of the MDCT coefficients were encoded by ECVQ_D4. Therefore, to obtain the optimal performance, the promotion of performance of ECVQ_D4 should be of the highest priority.
The calling ratios of the three component ECVQs in the nine testing items were demonstrated in Figure 6. It could also be observed that among all the nine items, the calling frequency of ECVQ_D4 was the highest, whereas the frequency of ECVQ_D1 was the lowest. As the vector dimensions ECVQ_D4, ECVQ_D2, and ECVQ_D1, were 4, 2, and 1, respectively, the calling rations of them implied that most of the MDCT coefficients in each testing item were encoded by the 4-dimensional ECVQ and only a very small amount of them were encoded by the 1-dimensional one. Through this way, FS-ECVQ achieved a relatively high coding performance. Furthermore, among all the nine items, the more frequently ECVQ_D4 was called, the larger coding gains the FS-ECVQ obtained. This explained why FS-ECVQ was more efficient in coding low bitrate items than the high bitrate ones.
4.5 ECVQ
As each component ECVQ contained two stages, lattice quantization and entropy coding, we would first assess the quantization stage and then, the entropy coding stage.
4.5.1 Quantization stage
To assess the quantization stage, we took LSB as a major indicator. There were at least three reasons. First, LSB appeared if and only if an input vector fell outside the range constrained by the lattice quantizer, and thus, LSB could be seen as the sign of the appearance of error in the quantization stage. Therefore, the lower occurrence frequency of LSB would usually denote fewer quantization errors in the quantization stage, and as a result, a higher coding gain achieved by the component ECVQ. Second, by adjusting the threshold T b d and T a c , we could achieve different occurrence frequency of LSB and thus make different trade-off between the coding gain and the memory requirements. At last, the ratio among the three LSB occurrence frequencies is correlated with the distribution of quantization errors among the three component ECVQs. A higher LSB occurrence frequency denoted more quantization errors distributed to the corresponding component ECVQ.
The LSB occurrence in each component ECVQ significantly influenced the final coding gain of the FS-ECVQ, which could be seen from the Table 5. For an input vector, if the LSB appeared, the ECVQ would consume much more bits than that for encoding it directly. There were two methods for reducing the appearance of LSB: to enlarge the range of the corresponding codebook or to shrink the range constrained by the threshold. However, the first method would lead to an increase in the memory requirements, while the second would degrade the coding gain. Therefore, a trade-off must be made between the memory requirements and the coding gain. Among the three ECVQs, ECVQ_D4 had the least percentage of LSBs while ECVQ_D1 had the largest. By this means, the FS-ECVQ could save the memory requirements while keeping the coding gain as high as possible.
4.5.2 The length functions
In each component ECVQ, the length function was realized by an arithmetic coder, which employed the sub-FSVQ to search for the optimum in a predesigned cdf model collection. The cdf models of FINAL and FS-ECVQ were demonstrated in Figure 7. From the figure, it could be seen that the cdf model numbers of the FINAL and FS-ECVQ were 64 and 85, respectively. Essentially, the cdf models contained were used to fit the pdf of the MDCT coefficient sequence. A larger number of cdf models generally would provide a higher accuracy fitting of the source pdf. Therefore, the FS-ECVQ could obtain a higher performance than the FINAL, theoretically.
Although the FINAL contained less cdf models than the FS-ECVQ did, it obtained similar coding performance to the FS-ECVQ. This was mainly owing to the cdf model selection method used in FINAL, which accurately selected the optimal cdf model for each input vector index. However, it was more complicated than that used in FS-ECVQ. This could be seen from the fact that the memory requirements for the cdf model selection in FINAL was much larger than those in FS-ECVQ, as demonstrated in Table 1.
5 Conclusions
In this paper, an ECVQ with finite memory, called FS-ECVQ, is proposed. In the FS-ECVQ, a FSVQ, namely the main FSVQ, is used to partition the source sequence into multiple non-overlapped clusters. Then to each cluster, an ECVQ is applied. Within each ECVQ, its length function is taken by an arithmetic coder holding multiple predesigned cdf models. To select the optimal cdf model for each input vector, another FSVQ, namely the sub-FSVQ, is employed.
Owing to the main FSVQ which effectively exploits the inter-frame dependencies, the source sequence is split into multiple clusters and no side information is needed to be transmitted. Moreover, the main FSVQ assigned different vector dimensions to the resulting clusters. The more frequently a cluster appears, the higher vector dimension is allocated. This helps the FS-ECVQ to efficiently reduce its total memory requirements while, at the same time, maintaining a relatively high coding performance. Finally, for each input vector, the sub-FSVQ selects the best matching cdf model, which adds robustness to the FS-ECVQ.
There are multiple ways to realize the proposed FS-ECVQ. First of all, if the quantizing errors generated from the lattice quantizer are directly discarded, then the FS-ECVQ is equivalent to an ordinary ECVQ. However, if the quantizing errors are taken as the LSBs and encoded by an additional length function, the FS-ECVQ will be equal to an uniform quantizer. In addition, if the quantization steps of all the component ECVQs are separated from the FS-ECVQ, then the FS-ECVQ becomes an entropy encoder. The FS-ECVQ can also be used in coding the speech, image, and video signals, and even any other source sequence with non-uniform distribution.
References
Gersho A, Gray RM: Vector Quantization and Signal Compression. New York: Wiley; 1994.
So S, Paliwal KK: Efficient product code vector quantisation using the switched split vector quantiser. Digit Signal Process 2007, 17: 138-171. 10.1016/j.dsp.2005.08.005
Gray R, Neuhoff D: Quantization. Inform. Theory, IEEE Trans 1998, 44(6):2325-2383. 10.1109/18.720541
Subramaniam A, Rao B: PDF optimized parametric vector quantization of speech line spectral frequencies. Speech Audio Process IEEE Trans 2003, 11(2):130-142. 10.1109/TSA.2003.809192
So S, Paliwal K: Multi-frame GMM-based block quantisation of line spectral frequencies for wideband speech coding. In Proceedings in IEEE International Conference on Acoustics, Speech, and Signal Processing, (ICASSP ’05), vol. 1. Philadelphia; March 2005:121-124.
Paliwal K, Atal B: Efficient vector quantization of LPC parameters at 24 bits/frame. Speech Audio Process IEEE Trans 1993, 1: 3-14. 10.1109/89.221363
Bouzid M, Cheraitia S, Hireche M: Switched split vector quantizer applied for encoding the LPC parameters of the 2.4 Kbits/s MELP speech coder. In 7th International Multi-Conference on Systems Signals and Devices. Amman, Jordan; June 2010:1-5.
Leis J, Sridharan S: Adaptive vector quantization for speech spectrum coding. Digit Signal Process 1999, 9(2):89-106. 10.1006/dspr.1999.0335
Chatterjee S, Sreenivas T: Optimum switched split vector quantization of LSF parameters.Signal Process.. 2008, 88(6):1528-1538.
Nordin F, Eriksson T: On split quantization of LSF parameters. In Proceedings on IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ’04), vol. 1. Montreal; May 2004:I-157–60.
So S, Paliwal KK: A comparative study of LPC parameter representations and quantisation schemes for wideband speech coding. Digit Signal Process 2007, 17: 114-137. 10.1016/j.dsp.2005.10.002
Chatterjee S, Sreenivas T: Gaussian mixture model based switched split vector quantization of LSF parameters. In IEEE International Symposium on Signal Processing and Information Technology. Giza; December 2007:1054-1059.
Lee Y, Jung W, Kim MY: GMM-based KLT-domain switched-split vector quantization for LSF coding. Signal Process Lett. IEEE 2011, 18(7):415-418.
Chatterjee S, Sreenivas T: Switched conditional PDF-based split VQ using gaussian mixture model. Signal Process Lett. IEEE 2008, 15: 91-94.
Chou P, Lookabaugh T, Gray R, Entropy-constrained vector quantization: Acoustics Speech Signal Process. IEEE Trans. 1989, 37: 31-42.
Lookabaugh T, Gray R: High-resolution quantization theory and the vector quantizer advantage. Inform Theory IEEE Trans 1989, 35(5):1020-1033. 10.1109/18.42217
Zhao D, Samuelsson J, Nilsson M: On entropy-constrained vector quantization using gaussian mixture models. Commun IEEE Trans 2008, 56(12):2094-2104.
Vasilache A: Rate-distortion models for entropy constrained lattice quantization. In IEEE International Conference on Acoustics Speech and Signal Processing, (ICASSP ’10). Dallas; March 2010:4698-4701.
Foster J, Gray R, Dunham M: Finite-state vector quantization for waveform coding. Inform Theory IEEE Trans 1985, 31(3):348-359. 10.1109/TIT.1985.1057035
Andras Cziho BS, ETC IL: An optimization of finite-state vector quantization for image compression. Signal Process Image Commun 2000, 15(6):545-558. 10.1016/S0923-5965(99)00012-0
Yahampath P, Pawlak M: On finite-state vector quantization for noisy channels.Commun. IEEE Trans 2004, 52(12):2125-2133. 10.1109/TCOMM.2004.838736
Chang RF, Huang YL: Finite-state vector quantization by exploiting interband and intraband correlations for subband image coding. Image Process IEEE Trans 1996, 5(2):374-378. 10.1109/83.480773
Jiang S, Yin R, Liu P: A finite-state entropy-constrained vector quantizer for audio MDCT coefficients coding. In International Conference on Audio, Language and Image Processing, (ICALIP 2012). Shanghai; July 2012:218-223.
ISO/IEC JTC1/SC29/WG11: Call for proposals on unified speech and audio coding. 2007.http://mpeg.chiariglione.org/standards/mpeg-d/unified-speech-and-audio-coding []
Gray R, Linder T, Li J: A Lagrangian formulation of Zador’s entropy-constrained quantization theorem. Inform Theory IEEE Trans 2002, 48(3):695-707. 10.1109/18.986007
Nasrabadi N, Rizvi S: Next-state functions for finite-state vector quantization. Image Process IEEE Trans 1995, 4(12):1592-1601. 10.1109/83.475510
Gray R, Li J: On Zador’s entropy-constrained quantization theorem. In Proceedings on Data Compression Conference, (DCC 2001). Snowbird; March 2001:3-12.
Gray R, Linder T: Mismatch in high-rate entropy-constrained vector quantization.Inform. Theory IEEE Trans 2003, 49(5):1204-1217. 10.1109/TIT.2003.810637
Fuchs G, Subbaraman V, Multrus M: Efficient context adaptive entropy coding for real-time applications. In IEEE International Conference on Acoustics, Speech and Signal Processing, (ICASSP ’11). Prague; May 2011:493-496.
Nasrabadi N, Choo C, Feng Y: Dynamic finite-state vector quantization of digital images. Commun IEEE Trans 1994, 42(5):2145-2154. 10.1109/26.285150
Gyorgy A, Linder T, Chou P, Betts B: Do optimal entropy-constrained quantizers have a finite or infinite number of codewords. Inform Theory IEEE Trans 2003, 49(11):3031-3037. 10.1109/TIT.2003.819340
Yu R, Lin X, Rahardja S, Ko C: A statistics study of the MDCT coefficient distribution for audio. In IEEE International Conference on Multimedia and Expo, (ICME ’04) vol. 2. Taipei; June 2004:1483-1486.
Popat K, Picard R: Cluster-based probability model and its application to image and texture processing. Image Process IEEE Trans 1997, 6(2):268-284. 10.1109/83.551697
ISO/IEC JTC 1/SC 29N11510: Information technology - MPEG audio technologies Part 3: unified speech and audio coding. 2010.http://mpeg.chiariglione.org/standards/mpeg-d/unified-speech-and-audio-coding []
Neuendorf M, Gournay P, Multrus M, Lecomte J, Bessette B, Geiger R, Bayer S, Fuchs G, Hilpert J, Rettelbach N, Salami R, Schuller G, Lefebvre R, Grill B: Unified speech and audio coding scheme for high quality at low bitrates. In IEEE International Conference on Acoustics, Speech and Signal Processing, (ICASSP ’09). Taipei; April 2009:1-4.
Acknowledgements
The authors wish to thank the anonymous reviewers for their detailed comments and suggestions, which have been extremely helpful in improving the clarity and quality of this paper. This work was supported by the National Natural Science Foundation of China under Grant No. 61171171.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jiang, S., Yin, R. & Liu, P. A memory efficient finite-state source coding algorithm for audio MDCT coefficients. J AUDIO SPEECH MUSIC PROC. 2014, 22 (2014). https://doi.org/10.1186/1687-4722-2014-22
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-4722-2014-22
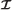 is a countable index set. Each element in
is a countable index set. Each element in 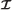 corresponds to a different codevector contained in codebook
corresponds to a different codevector contained in codebook 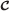 . The aim of encoder ϕ is to find the index of the best matching vector in codebook
. The aim of encoder ϕ is to find the index of the best matching vector in codebook 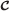 for input vector x according to a given distortion criterion
for input vector x according to a given distortion criterion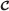 , which is used by both encoder ϕ and decoder ψ to generate the optimal codevector indices or to find the corresponding codevectors
, which is used by both encoder ϕ and decoder ψ to generate the optimal codevector indices or to find the corresponding codevectors





