- Research Article
- Open access
- Published:
Environmental Sound Perception: Metadescription and Modeling Based on Independent Primary Studies
EURASIP Journal on Audio, Speech, and Music Processing volume 2010, Article number: 362013 (2010)
Abstract
The aim of the study is to transpose and extend to a set of environmental sounds the notion of sound descriptors usually used for musical sounds. Four separate primary studies dealing with interior car sounds, air-conditioning units, car horns, and closing car doors are considered collectively. The corpus formed by these initial stimuli is submitted to new experimental studies and analyses, both for revealing metacategories and for defining more precisely the limits of each of the resulting categories. In a second step, the new structure is modeled: common and specific dimensions within each category are derived from the initial results and new investigations of audio features are performed. Furthermore, an automatic classifier based on two audio descriptors and a multinomial logistic regression procedure is implemented and validated with the corpus.
1. Introduction
The purpose of this study is to transpose and extend the timbre description principles from musical sounds to environmental sounds, which are by nature considered as nonmusical. More precisely, environmental sounds were first defined by Vanderveer [1] as " any possible audible acoustic event which is caused by motions in the ordinary human environment. (⋯) Besides (
any possible audible acoustic event which is caused by motions in the ordinary human environment. (⋯) Besides ( ) having real events as their sources (⋯), (
) having real events as their sources (⋯), ( ) [they] are usually more "complex'' than laboratory sinusoids, (⋯), (
) [they] are usually more "complex'' than laboratory sinusoids, (⋯), ( ) [they] are meaningful, in the sense that they specify events in the environment. (⋯), (
) [they] are meaningful, in the sense that they specify events in the environment. (⋯), ( ) the sounds to be considered are not part of a communication system, or communication sounds, they are taken in their literal rather than signal or symbolic interpretation."
) the sounds to be considered are not part of a communication system, or communication sounds, they are taken in their literal rather than signal or symbolic interpretation."
Within the restricted framework given by the scope of the primary research upon which the present study is based (see Section 2), the final aim is also to automate indexing and classification of environmental sounds. This goal is actually essential for sound quality measurement, as well as for further sound-content-based searching and browsing methods that use perceptual models of environmental sounds and often require measurements based on perceptually relevant acoustical similarities. Indeed, in the sound-quality field, most studies use acoustical/psychoacoustic descriptors such as loudness or roughness in order to explain unpleasantness ratings, whereas several studies have shown that no "universal'' descriptors exist for all classes of everyday sounds.
The work detailed in this article starts from four primary industrial studies on sound attributes dealing with sounds produced by car engines (Susini et al. [2–4], McAdams et al. [5]), air-conditioning units (Susini et al. [6]), car horns (Lemaitre et al. [7, 8]), and closing car doors (Parizet et al. [9]). The aim of these studies was to apply the methodology developed to study the timbre of musical sounds to a specific category of environmental sounds. The standard methodology used in these studies was based on a multidimensional scaling technique (MDS) applied to dissimilarity ratings.
The MDS technique is a fruitful tool for studying perceptual relationships among sounds and for determining the underlying auditory attributes used by participants to rate the perceived similarities among sounds. The term auditory attribute is used to describe the perceived properties or qualities of the sounds. Well-known auditory attributes include loudness, pitch, duration, sharpness, and so forth. The MDS technique does not require a priori assumptions concerning the number of auditory attributes or their nature, unlike semantic differential methods that use ratings along specific dimensions, such as roughness, for example. The MDS technique represents the perceived similarities in a low-dimensional Euclidean space (referred to as the perceptual space), so that the distances among the stimuli reflect the perceived dissimilarities. Each dimension of the space (called a perceptual dimension) is assumed to correspond to a perceptual continuum that is common to the whole set of sounds. Thus the main hypothesis with the MDS technique is that the sounds under study can be compared on auditory attributes that are shared by all sounds in the corpus. In other words, this technique is appropriate for characterizing sounds that are comparable along continuous auditory attributes of a homogenous corpus composed of sounds produced by the same type of source (musical instruments, car sounds, vacuum cleaner noises, etc.). Considering musical sounds, the most common timbre space found by several studies (among which Grey [10], Krumhansl [11], McAdams et al. [12], and Marozeau et al. [13]) consisted of three dimensions correlated with acoustic features in order to associate a measurable sound parameter with each perceptual dimension of timbre. The assumption of this approach rests on the model suggested by McAdams [14], who postulates that the recognition of sound sources arises from a process of analysis, computation, and extraction of a certain number of auditory features related to the acoustic parameters of the signals. Then, in many of these musical timbre studies, the three dimensions were found to be significantly correlated with a spectral feature that most often represented auditory brightness (energy distribution along the frequency scale), a temporal feature that characterized attack, and a spectro-temporal feature corresponding to spectral variations over time. The MDS technique has been shown to be an efficient tool for revealing and describing the previously unknown auditory attributes underlying the timbre of musical sounds.
In the present context, environmental sound studies, experimental data, analyses, and acoustic parameters have been reviewed and compared from the four initial studies. An investigation of these combined data was conducted, and an attempt to model the resulting structures on the basis of the primary results was made using generalized toolboxes (essentially, "Ircamdescriptor" from Peeters [15] and "Auditory Toolbox" from Slaney [16]) in order to unify—and in some cases to improve—the description of the initial data. Here we will first introduce and describe all the studies taken into account in this review, their stimulus sets, the experiments performed, the resulting perceptual spaces, and the correlated acoustic features. Then, in order to contribute to environmental sound perception, we will first present the organization of this global stimulus set in terms of the main environmental sound classes, propose both interclass and intraclass structure descriptions, and finally initiate an automatic classification modeling approach within the restricted scope of the present study, but on the basis of perceptually relevant data and results gathered during its experimental parts.
2. Primary Studies
We present in this section the frameworks, motivations, and results of the four experimental studies that represent the starting point of our metaanalysis. These studies focus on the sounds from:
- (A)
-
(B)
Interior air-conditioning units (Susini et al. [6]),
- (C)
-
(D)
Closing car doors (Parizet et al. [9]).
These four studies all addressed the issue of sound quality and shared a common approach: they studied the timbre of the different types of sounds. More precisely, they used a common methodology and shared similar analysis techniques. This procedure relies on the psychoacoustic definition of timbre: "Timbre is that attribute of auditory sensation in terms of which a listener can judge that two sounds similarly presented and having the same loudness and pitch are dissimilar.'' (American national standard acoustical terminology (1994). American National Standards Institute, ANSI S1.1-1994 (R1999); see also Krumhansl [11]). Timbre is thought to be multidimensional, encompassing several perceptual attributes that are collectively referred to by this term. In order to uncover the attributes of timbre, the methodology used in the studies was based on the procedure developed to study the timbre of musical sounds (McAdams et al. [12]). It has three main steps, the first one being sometimes preceded by a preliminary step (labeled "0'' below) used to reduce the number of sounds to be tested in the first step.
-
(0)
Because the following step of the methodology needs a small number of sounds to be experimentally feasible, a preliminary step is sometimes used in order to reduce the original corpus to an acceptable number of stimuli (usually not more than 20 samples). Free-sorting tasks and cluster analyses (see Section 3.1 for further details) are used to attain this goal. A free-sorting task consists in asking participants to sort the sounds of the set into as many categories as they wish. Thus, they identify the main categories of sounds that are studied and allow for the selection of representative subsets of sounds by homogeneously sampling across the categories.
-
(1)
A dissimilarity rating experiment collects the perceived dissimilarities among the sounds, which are then used as proximity data. It consists in asking the participants to rate directly the dissimilarity between both sounds of each possible pair within the set of sounds. The evaluation is made on a continuous scale labelled "Very Similar" at the left end and "Very Dissimilar" at the right end. It has the great advantage that it does not impose any predefined rating criteria on the listener.
-
(2)
The proximity data are modeled with a multidimensional scaling (MDS) analysis that fits distances in a geometrical space to the dissimilarity data. The dimensions of this space represent the perceptual dimensions underlying the proximities. Different levels of complexity exist in the MDS approach depending on the model and associated algorithm (see Appendix A); in the present case, two particular MDS techniques were used in the studies: the INDSCAL (Individual Differences Scaling) and CLASCAL (Latent-Class Approach) models.
-
(3)
The final step of a timbre study is to give a physical interpretation of the perceptual dimensions revealed by the MDS analysis. This is usually done by submitting the perceptual dimensions to linear regression analyses with relevant acoustic features. Some of them are psychoacoustic descriptors, that is, acoustic features that have been found to correspond to auditory sensations. Models that compute psychoacoustic descriptors are usually based on a model of the peripheral auditory system.
2.1. Studies A (A1, A2). Car Interior [2–5]
2.1.1. Context
The main goal of this study was to analyze the timbre of the sounds of car interiors in a given driving condition from the driver/passenger point of view.
2.1.2. Stimuli
The sounds were recorded in 16 different vehicles at two different engine modes. The engine modes defined two substudies: study A1 involved sounds produced when the engine was running in 3rd gear at 4000 RPM (Round Per Minute) and study A2 involved sounds produced when the engine was running in 5th gear at 3500 RPM. A preliminary experiment showed that loudness was the main auditory cue used by the participants to rate the dissimilarity. Thus, in order to let other auditory attributes emerge, loudness was equalized. Both stimulus sets were composed of 16 stereophonic sounds that were 4.1 seconds in duration. Their levels—after loudness equalization—varied between 69 and 80 dB SPL (Sound Pressure Level).
2.1.3. Participants
For each engine mode stimulus set, a dissimilarity rating experiment was conducted with 30 participants.
2.1.4. Analysis and Results for Study A1
A CLASCAL analysis (see Appendix A) of the data yielded a 1-latent class, 3-dimensional space with specificities. Figures 13(a) to 13(c) represent the projections of the space, and Table 9 reports the correlation coefficients of the acoustic features best fitting the perceptual dimensions. The first dimension is correlated [ ,
,  ] with a feature corresponding to the relative balance of the harmonic (motor) and noise (air turbulence) components. The second dimension is correlated [
] with a feature corresponding to the relative balance of the harmonic (motor) and noise (air turbulence) components. The second dimension is correlated [ ,
,  ] with a variation of the spectral centroid with the frequency dimension represented in ERB-rate (see Appendix B for more details). The third dimension is significantly correlated [
] with a variation of the spectral centroid with the frequency dimension represented in ERB-rate (see Appendix B for more details). The third dimension is significantly correlated [ ,
,  ] with an acoustic feature quantifying the spectral decrease of the harmonic part of the sound.
] with an acoustic feature quantifying the spectral decrease of the harmonic part of the sound.
2.1.5. Analysis and Results for Study A2
A CLASCAL analysis (see Appendix A) yielded a 1-latent class, 2-dimensional space with specificities. Figure 14 represents the perceptual space and Table 10 reports the correlation coefficients of the acoustic features best fitting the perceptual dimensions; the features that are the best correlated with the two dimensions are also reported in Table 10. The first dimension is correlated [ ,
,  ] with an acoustic feature conveying the relative balance between two groups of partials of the harmonic part of the signal (see Appendix B for more details). The second dimension is correlated [
] with an acoustic feature conveying the relative balance between two groups of partials of the harmonic part of the signal (see Appendix B for more details). The second dimension is correlated [ ,
,  ] with the spectral centroid computed on the C-weighted version of the signal (see Appendix B for more details).
] with the spectral centroid computed on the C-weighted version of the signal (see Appendix B for more details).
2.2. Study B. Interior Air-Conditioning Units [6]
2.2.1. Context
This study focused on the sound quality of interior air-conditioning units.
2.2.2. Stimuli
The initial set consisted of 43 sounds produced by units of different brands. A free-sorting experiment was first conducted to select an homogeneous subset of sounds representative of the existing range for this type of sounds. The results of this experiment also showed that three categories were made mainly by grouping together sounds with similar loudness levels. As in study A, in order to prevent loudness from dominating the ratings (possibly masking more subtle effects), the sounds were selected in the category corresponding to a medium loudness level (average level: 46.5 dB SPL, 2.2 dB standard deviation). An informal experiment was then performed with only 5 participants to get an initial estimate of the perceptual space structure. The outcome of the MDS analysis was that the space was not homogeneously sampled. Therefore, synthesized sounds were added and redundant sounds were removed in order to produce a more homogeneously distributed stimulus set. The synthesized sounds were created on the basis of features of the sounds in the stimulus set, using a geometric interpolation within the space. The resulting stimulus set consisted of 19 sounds: 15 recordings of air-conditioning units and 4 synthesized sounds. They were all 5.9 seconds in duration with levels varying between 44 and 52 dB SPL.
2.2.3. Participants
The dissimilarity rating experiment was conducted with 50 participants.
2.2.4. Analysis and Results
A CLASCAL analysis (see Appendix A) of the dissimilarity ratings yielded a 5-latent class, 3-dimensional space with specificities. Figures 15(a) to 15(c) represent the projections of the 3-dimensional space, and Table 11 presents the correlation coefficients of the features that are the best correlated with the perceptual dimensions. The first dimension is correlated [ ,
,  ] with a feature corresponding to the relative balance of the harmonic (motor) and noise (air turbulence) components. The second dimension is correlated with a frequency-weighted variation of the spectral centroid of the noise component [
] with a feature corresponding to the relative balance of the harmonic (motor) and noise (air turbulence) components. The second dimension is correlated with a frequency-weighted variation of the spectral centroid of the noise component [ ,
,  ]. The third dimension is correlated with loudness [
]. The third dimension is correlated with loudness [ ,
,  ]. Indeed, even though the selected sounds are in the same range of loudness, they were not equalized in loudness.
]. Indeed, even though the selected sounds are in the same range of loudness, they were not equalized in loudness.
2.3. Study C. Car Horns [7, 8]
2.3.1. Context
This study concerned the timbre of car horns in order to define specifications for the design of new sounds. The initial stimulus set consisted of 43 recordings of current car horn sounds. These sounds can be either monophonic (one note) or polyphonic (two or three notes to make a chord) and are produced by two different mechanisms: a metal plate or a folded horn that acts as a resonator and is attached to the membrane of an electroacoustic driver. Both produce very specific timbres. A preliminary sorting experiment highlighted 9 main categories of sounds connected with these different mechanisms and properties.
2.3.2. Stimuli
A sample of 22 sounds was chosen among the 9 categories. Among these 22 sounds, 13 were monophonic and 9 were polyphonic, 10 were produced by "plate" resonators and 12 by "horn" resonators. All sounds lasted between 0.6 and 2.2 seconds. Their levels varied between 63 and 77 dB SPL.
2.3.3. Participants
A dissimilarity rating experiment using this set of sounds was conducted with 41 participants.
2.3.4. Analysis and Results
The dissimilarity ratings were submitted to a CLASCAL analysis (see Appendix A), resulting in a 6-latent class, 3-dimensionial space with specificities. Figures 16(a) to 16(c) represent the projections of the 3-dimensional space, and Table 12 reports the best-correlated features (see [7], for more details on the acoustic features). The first dimension is correlated [ ,
,  ] with roughness. The second dimension is correlated [
] with roughness. The second dimension is correlated [ ,
,  ] with a variation of the spectral centroid integrating a perceptual approach to compute this parameter (ERB scale, see Marozeau et al. [13]). The third dimension is correlated [
] with a variation of the spectral centroid integrating a perceptual approach to compute this parameter (ERB scale, see Marozeau et al. [13]). The third dimension is correlated [ ,
,  ] with an acoustic feature related to the fine structure of the spectral envelope.
] with an acoustic feature related to the fine structure of the spectral envelope.
2.4. Study D. Car Door Closing [9]
2.4.1. Context
The main goal was to study the timbre of car door closing sounds in the context of evaluating their sound quality.
2.4.2. Stimuli
An initial set of 27 stereophonic recordings (16 sounds from different cars and 11 sounds from two cars with modified seals) was submitted to a sorting experiment with 31 participants in order to select a representative subset of 12 sounds. Among these 12 sounds, 4 were recorded from cars with modified seals. The durations of the sounds varied between 0.3 and 0.5 seconds, and their levels varied between 66 and 84 dB SPL.
2.4.3. Participants
A dissimilarity rating experiment was conducted with 40 participants.
2.4.4. Analysis and Results
The dissimilarity data were submitted to an INDSCAL analysis (see Appendix A). A 3-dimensional space was found. Figures 17(a) to 17(c) represent its projections, and Table 13 reports the correlation coefficients of the features best correlated with the perceptual dimensions. The first dimension is correlated with a feature corresponding to sharpness, as defined by Aures [17] [ ,
,  ], as well as to the spectral centroid [
], as well as to the spectral centroid [ ,
,  ]. The second dimension is correlated [
]. The second dimension is correlated [ ,
,  ] with an indicator related to the temporal evolution of instantaneous loudness, according to Zwicker's model [18]. No descriptor was found that correlated significantly with the third dimension.
] with an indicator related to the temporal evolution of instantaneous loudness, according to Zwicker's model [18]. No descriptor was found that correlated significantly with the third dimension.
2.5. Comparisons and Discussion
The studies reported in the previous subsections identify the perceptual space of sounds contained in five separate stimulus sets (labelled A1, A2, B, C and D), associated with different kinds of environmental situations, mainly related to car and appliance industries. The results of these studies are summarized in Table 1.
A comparison of the acoustic features correlated with the dimensions of these four perceptual spaces yields some interesting facts.
-
(i)
In every study, at least one dimension in the perceptual space resulting from the MDS analysis is found to be related to a spectral centroid feature, usually describing the "brightness'' of a sound. This "brightness'' attribute seems therefore incontrovertible when trying to compare two sounds of any of these kinds of sources. However, this attribute seems to take different forms across the studies.
-
(a)
It can be computed with a frequency weighting representing the variation in sensitivity of the human ear over the audible frequency range at different presentation levels (A-, B-, and C-weightings).
-
(b)
It can introduce a much more sophisticated model of the hearing process (ERB filters).
-
(c)
It is sometimes only computed on a particular part of the signal (noise part). The subsidiary questions are: will all these "brightness'' predictors be as efficient for all studies? If not, is there a particular calculation that fits all of the spaces equally well?
-
(a)
-
(ii)
In 3 studies, relevant acoustic features appear to include separate calculations for the harmonic and noise parts of the signals. The signal processing needed for this separation is quite complex and often includes the setting of several initial algorithm parameters. Again, the question raised is as follows: will a common set of these parameters result in the same efficiency of separation for the correlation scores in the 3 studies?
-
(iii)
For the 2 other studies, the correlation results exhibit specific relevant acoustic features. This fact confirms that a universal low-dimensional perceptual space describing all sounds does not exist. It would also tend to agree with McAdams et al. [5] and McAdams [19] who observed that when sounds are produced by classes of sources that are too different the dissimilarity judgments may be based on cognitive factors rather than on perceptual signal-related ones, which results in a strongly categorical description.
3. Metaprocessing: Complementary Experimental Investigations
The MDS technique is appropriate to characterize a set of sounds caused by very similar sound sources, but not for different and obviously identified sources. For instance, McAdams et al. [5] applied an MDS analysis to an extremely heterogeneous set of environmental sounds (trains, cars and planes). The analysis yielded a strongly categorical perceptual structure: listeners identified the sound sources rather than comparing them along continuous perceptual dimensions. In that case, participants based their perception on a predominant cognitive factors: recognition, classification, and identification of the sound source (see McAdams [19]). In other words, when the sounds under consideration are similar, which means that they are provided by the same type of sources, listeners are able to compare them on continuous perceptual dimensions otherwise they are categorized by association with the type of source. As a consequence, the perceptual organization of the five groups of stimuli may be based on a 2-level structure displaying both categorical and continuous levels (see Figure 1, for illustration):
-
(i)
a categorical (discrete) level corresponding to the main sound-event categories, each of them being related to a distinct physical cause or source,
-
(ii)
a continuous level that will associate each of these categories with a perceptual space with salient dimensions that can be either specific to the given category or shared with the others.
In order to evaluate the consistency of this structure and to validate it within the scope of the present research, an additional experimental investigation was conducted consisting of two successive experiments:
-
(1)
a free-sorting task to identify the main sound event categories composing the overall sound corpus, combined from the initial corpora presented in Section 2,
-
(2)
a forced-choice sorting task on more heterogeneous sounds (extracted from commercial sound libraries) in order to extend and determine more precisely the boundaries of these categories. The results of these experiments will then be used in the last part of the study (see Section 4) in order to define new ways of modeling the structure on both discrete and continuous levels, as defined in our hypothesis, that describe the main sound-event categories and perceptual dimensions attached to each of those categories, respectively.
3.1. Experiment: Free-Sorting Task on the Initial Corpora
In order to identify the main perceptual categories among the sounds under consideration in this study, a free-sorting experiment with this complete stimulus set was conducted.
3.1.1. Method
Participants
Twenty participants (8 women and 12 men) volunteered as listeners for this experiment and were paid for their participation. All reported having normal hearing.
Stimuli
The resulting unified stimulus set is a collection of 83 sounds distributed as follows: 16, 14, 19, 22, and 12 sounds from studies A1, A2, B, C, and D, respectively. See Sections 2.1.2, 2.2.2, 2.3.2, 2.4.2 for more details on the sounds. In order to prevent the listeners from sorting the sounds according to their loudnesses, a preliminary loudness-equalization experiment was conducted with 7 participants working at IRCAM, resulting in an 83-sound loudness-equalized corpus.
Apparatus
Testing took place in a double-walled IAC sound-isolation booth. The sounds were played over Sennheiser HD 520 II headphones through an RME Fireface 400 audio card plugged into a Macintosh Mac Pro (Mac OS X v10.4 Tiger) workstation. The test was run using a Graphical User Interface (GUI) developed by Vincent Rioux in Matlab (v7.0.4) including stimulus control, data recording, and sound play-back.
Procedure
At the beginning of the procedure, the participants were given written instructions briefly presenting the context of the study and detailing the task to be performed. The task was to classify the 83 sounds of the corpus into as many categories as they wished according to their own criteria and, in a second step, to select the most representative sound—the prototype—for each of the classes (see Section 3.2 for the definition of a prototype by Rosch [20]). In the GUI, the sounds were represented as dots that could be either played (double-click) or moved (drag and drop) to the dedicated area of the screen in order to graphically compose the categories (see Figure 18 for an illustration of the interface).
3.1.2. Results
Analysis
The experimental data consist of individual incidence matrices (coding the set partitions of each subject) that are summed to form a cooccurrence matrix. The cooccurrence matrix represents how many subjects have placed each pair of sounds in the same category. This can also be interpreted as a proximity matrix (Kruskal and Wish [21]). In the present case, we derived a hierarchical tree representation from these data using an unweighted arithmetic average clustering (UPGMA) analysis algorithm (see P. Legendre and L. Legendre [22] for computational details). In such a representation, the distance between two sounds is represented by the height of the node that links them. Among the 91,881 triplets that can be formed out of 83 sounds, 94% follow the ultrametric inequality, which shows the adequacy of the tree representation for these data (see P. Legendre and L. Legendre [22]). The tree representation is shown in Figure 2. It can be clearly seen that 3 main categories constitute the unified corpus. Looking in detail at the items inside each of them, we can observe that these 3 categories correspond, respectively, to studies A and B (right part of Figure 2), study C (left part of Figure 2), and study D (middle part of Figure 2). Moreover, listening to these items led us to propose a semantic labeling for each of these 3 categories: "motor,'' (musical) "instrument-like,'' and "impact,'' respectively.
We subsequently extracted the prototypic sound for each of the 3 categories by a specifically developed algorithm. Each listener selected prototypes with regard to her/his own categories, which are not necessarily the 3 categories extracted from the cluster analysis. Consequently, we had to consider the prototype selection for each pair of sounds, as follows.
-
(i)
For each pair of sounds in an individual 83
 83 matrix, if sound j was selected by a listener as prototype of a category that contains sound
83 matrix, if sound j was selected by a listener as prototype of a category that contains sound  , then cell
, then cell  is incremented (but not cell
is incremented (but not cell  ).
). -
(ii)
After summing the matrix over the panel of listeners, a submatrix is extracted for each of the 3 final categories with the rows and lines indexed by the sounds constituting the category.
-
(iii)
Each submatrix is averaged over its rows, and the highest score gives the index of the prototype.
With this method, the selection by a listener of a sound as prototype for sounds that do not belong to the same final category does not influence the final selection of prototypes. The 3 selected sounds will be used in Experiment  (Section 3.2) to define the 3 categories.
(Section 3.2) to define the 3 categories.
Discussion
As a result, the five initial corpora can be reorganized into 3 main categories on the basis of the perceptual results (Experiment  ). Obviously, these categories are strongly defined by the initial studies from which they were drawn. In other words, there is no overlap between the initial corpora and the final structure: studies A1, A2, B belong to a first category, study C to a second category and study D to a third one. However, this fact was intuited before the experiment just by listening to the sounds. According to the sound production type, we semantically defined these categories as follows:
). Obviously, these categories are strongly defined by the initial studies from which they were drawn. In other words, there is no overlap between the initial corpora and the final structure: studies A1, A2, B belong to a first category, study C to a second category and study D to a third one. However, this fact was intuited before the experiment just by listening to the sounds. According to the sound production type, we semantically defined these categories as follows:
-
(i)
"motor'' (first category): sounds from both car interior (studies A1 and A2) and air-conditioning unit (study B) corpora. These sounds have two discriminable components: a harmonic part with a quite low fundamental frequency produced by a "motor" and a noisy part produced by air turbulence;
-
(ii)
"instrument-like'' (second category): sounds that correspond to the car horn corpus (study C), which are defined by one or several higher tones, closer to those produced by musical instruments than those generated by motors;
-
(iii)
"impact'' (third category): sounds of the car door closing corpus (study D). Actually, one can easily discriminate these sounds from the others because of their temporal structure. This idea is consistent with the discrimination of percussive and sustained sounds among musical timbres. Indeed, impact sounds of the environment are quite close to musical percussive sounds in terms of sound production.
This categorization is consistent with the product sound classification proposed by Özcan and van Egmond [23] defined by 6 sound categories: air, alarm, cyclic, impact, liquid, and mechanical. Even though these product sounds were from a domestic context, Özcan and van Egmond. found an impact category; they also found an alarm category that can correspond to the present instrument-like category with regard to basic similarities in pitch, harmonic structure, or stationary aspects of the sounds; and finally, the present motor category can be linked to both their air and mechanical categories.
3.2. Experiment 2: Forced-Choice Sorting Task on an Extended Corpus
On the basis of the previous results (3 main categories of environmental sounds within the scope of the unified corpus, with an associated prototype for each), a second experiment was conducted in order to generate a more heterogeneous corpus that would better represent the range of variation of each category. This was done by means of a forced-choice procedure, the main choices being the categories found in Experiment  . These 3 categories were each identified by their respective prototypic sound extracted from Experiment
. These 3 categories were each identified by their respective prototypic sound extracted from Experiment  , instead of being verbally defined as it is usually done in this kind of procedure. The notion of prototype is based on psychological principles related to the way one organizes knowledge of the surrounding world. For Rosch [20], a prototype is the element of a group that is the most similar to all items inside the group and, at the same time, that is on average the most different from items of all the other groups. The notion of prototype used in the present study is directly derived from Rosch's concept.
, instead of being verbally defined as it is usually done in this kind of procedure. The notion of prototype is based on psychological principles related to the way one organizes knowledge of the surrounding world. For Rosch [20], a prototype is the element of a group that is the most similar to all items inside the group and, at the same time, that is on average the most different from items of all the other groups. The notion of prototype used in the present study is directly derived from Rosch's concept.
Furthermore, the outcome of this second experiment will also provide perceptually validated data for the modeling part of the present study in order to implement an automatic classifier (see Section 4.2).
3.2.1. Method
Participants
Twenty-one participants (8 women and 13 men) volunteered as listeners for this experiment and were paid for their participation. All reported having normal hearing.
Stimuli
A new extended corpus was created on the basis of the main categories found in the previous experiment. Several sounds were added to each category in order to make the stimulus set more complete and heterogeneous. We therefore, chose various new sounds with quite extreme cases for each category from commercial sound libraries (Hollywood Edge Premiere Edition I, II and III, Sound Ideas General Series 6000 and Blue Box Audio Wav). Here are some examples of sounds added in each category:
-
(i)
for motor sounds: truck, aircraft, motorbike, helicopter, crane, vacuum cleaner, fridge, blender, electric shaver, lawn mower;
-
(ii)
for instrument-like sounds: phone ringing, dishes squeak, door creak, alarm, bell;
-
(iii)
for impact sounds: glass shock, various doors closing (fridge door, house door, etc.), computer keyboard, water drop, tennis ball.
Again, the sounds needed to be equalized in loudness so that the judgments would not be based on this auditory attribute. However, considering the high number of sounds, a preliminary experiment of loudness equalization would have been quite long. As a consequence, the sounds' loudnesses were equalized with regard to the value given by the loudness model of Zwicker and Fastl [24].
The final corpus was composed of 150 loudness-equalized sounds with an equal distribution of 50 sounds in each category.
Apparatus
The same technical equipment as in Experiment  was used. However, the study was run using a GUI specifically developed in the PsiExp v3.4 experimentation environment including stimulus control and data recording (Smith [25]). The sounds were played with Cycling74's Max/MSP software (v4.6).
was used. However, the study was run using a GUI specifically developed in the PsiExp v3.4 experimentation environment including stimulus control and data recording (Smith [25]). The sounds were played with Cycling74's Max/MSP software (v4.6).
Procedure
At the beginning of the experiment, the participants were given written instructions briefly presenting the context of the study and detailing the task to be performed. They were asked to classify the 150 sounds of the new corpus into 3 unnamed categories associated with their respective prototypical sounds by clicking on the corresponding button. A fourth button labeled "other'' allowed participants to not choose any of the 3 main categories (see Figure 19 for an illustration of the interface). The specificity of the present paradigm was to make the categories explicit with the prototype sounds found in Experiment  —with the obvious exception of the class "other''—instead of naming them directly. This implementation was chosen in order to avoid any ambiguity in the understanding of the arbitrary semantic attributes that did not result from verbalization analyses.
—with the obvious exception of the class "other''—instead of naming them directly. This implementation was chosen in order to avoid any ambiguity in the understanding of the arbitrary semantic attributes that did not result from verbalization analyses.
3.2.2. Results
Analysis
Table 2 presents the sound distribution, that is, mean and standard deviation of the number of sounds placed by the participants in each category. Note that these data are strongly influenced by the choices of sounds added by the experimenter, and that these numbers mainly show the adequacy or inadequacy of these choices. However, the following points may be emphasized.
-
(i)
The high standard deviation of the number of rejected sounds ("other") might be related to differences in strategy among the participants who did not use the same selectivity threshold, or the same granularity, to group the sounds.
-
(ii)
The high mean number of sounds combined with a relatively low standard deviation for the motors shows a consensus among the participants that proves the adequacy of the selection of sounds for this category.
-
(iii)
To the contrary, the relatively high standard deviations for the two other categories show some variability in the listeners' judgments, which is probably due to the quite large variety of chosen sounds for these categories. For the "instrument-like'' category, the variability seems to be related to the difficulty of theoretically defining this type of sound, whereas for the impacts, it could be explained by the overly general character of this category.
Nevertheless, after computing a percentage of belonging to the categories for each sound of the 150-item corpus, we observed that these disparities in classification were only concentrated on certain sounds, which were then rejected (26 sounds under a threshold of about 65% of belonging to a category). We thus obtained a selection of the extended corpus leading to a 124-sound stimulus set: 50 "motor,'' 27 "instrument-like,'' 47 "impact.'' Note that this final distribution corresponds roughly to that of Table 2.
Discussion
The partitioning of the data across the 3 categories shows a good consensus on a certain number of sounds for each class. With this result, we are then able to make a selection of sounds that are clearly associated with one of the 3 categories revealed in Experiment  . This leads to the constitution of a perceptually validated sound corpus with regard to the motor, instrument-like, and impact categories, which is now large and representative enough to consider the conception and validation of a predictive tool for automatic classification of environmental sounds in these three categories.
. This leads to the constitution of a perceptually validated sound corpus with regard to the motor, instrument-like, and impact categories, which is now large and representative enough to consider the conception and validation of a predictive tool for automatic classification of environmental sounds in these three categories.
3.3. Discussion
Within the restricted scope of environmental sounds studied here (industrial sounds from cars and machines), we are now faced with the following structure:
-
(i)
a motor category including 49 sounds from 3 different corpora (A1, A2, B), each of them being described by a perceptual space and augmented with 50 perceptually validated new sounds, for a total of 99 items,
-
(ii)
an instrument-like category including 22 sounds from corpus C described by a perceptual space and augmented with 27 perceptually validated new sounds, for a total of 49,
-
(iii)
an impact category including 12 sounds from corpus D described by a perceptual space and augmented with 47 perceptually validated new sounds, for a total of 59.
In the next step, this corpus will serve as input for the implementation of the automatic classifier detailed in Section 4.2.
4. Metaprocessing: Modeling the Description Structure
This section was designed to confirm the second part of the starting hypothesis, which stipulates that both intercategory and intracategory properties exist, that is, dimensions shared by the all categories and specific dimensions related to their mutual discriminating differences. Furthermore, the knowledge of these discriminating features could facilitate the implementation of a predictive tool capable of automatically recognizing whether a new item belongs to one of the 3 metacategories. Note that every acoustic feature mentioned in this section is extracted either from the Ircamdescriptor toolbox (CUIDADO project, Peeters [15]) or from the Auditory Toolbox (Slaney [16]).
4.1. Continuous Level: Unifying the Perceptual Space Dimensions
In this first part, we investigate the shared and specific properties across the categories by considering the data coming from the corpus described by perceptual space dimensions (corpuses A to D). The main idea is to unify these data by recomputing the acoustic features explaining the different perceptual dimensions in a more systematic manner, in order to point out regularities and singularities among the given spaces. The implementation of these acoustic features is detailed in Appendix D.
Note that some of the stimulus sets contain only monophonic sounds, whereas others contain only stereophonic sounds, and, although the acoustic features are calculated on both channels in the latter case, the salience of an indicator in one channel compared to the other depends on the recording context. For example, if a car interior sound has been recorded from the driver's seat, the most relevant channel for a given sound feature will probably not be the same as if it had been recorded from the passenger's seat. Accordingly, the features in the correlation tables can be either from the left or the right channel, or from the mean of both channels.
4.1.1. MDS Analyses Compatibility
The two models giving rise to the perceptual spaces that will be unified in this section are INDSCAL and CLASCAL (see Appendix A). As both models remove the rotational invariance of the obtained spaces, one could assume that both models would result in similar main perceptual dimensions (even if possible slight differences in the items' positions or the axes' orientations may be due to the precision of the model). However, the presence of specificities in the latter can modify the psychological meaning of the dimensions. Indeed, the fact that a part of the Euclidean distances is explained by those specificities leads to a modification of the proportion explained by the dimensions. Thus the dimensions obtained by both models will not necessarily be the same.
All the same, the only sound corpus for which the INDSCAL method was used (study D) corresponded to a different sound category than those of the other corpora (see Section 3.1). As a consequence, the fact that the dimensions were obtained differently from the other studies is not a problem. Indeed, this perceptual space will be studied separately from the others.
4.1.2. Motor Category
One of the main characteristics of this kind of sound is that it contains two different simultaneous parts. The first one corresponds to a harmonic pattern that can be easily modeled by a sum of sinusoids, and the second one corresponds to the noise resulting from the air turbulence. Perceptually, these two parts are highly discriminable. Consequently, unlike the other two categories, both parts need to be taken into account independently when estimating the acoustic features. This is the reason why harmonic separation methods were tested and used in order to describe both parts, as well as their mutual interaction.
This metacategory regroups stimulus sets A1, A2 and B, presented in Sections 2.1 and 2.2. Those stimulus sets' MDS analyses resulted in 3-dimensional perceptual spaces, except for that of study A2, which gave a 2-dimensional space. Because of the relative proximity of the sounds coming from these 3 stimulus sets, two shared dimensions were found. The first one is related to the harmonic/noise ratio, while the second is related to the spectral centroids of both parts with some interactions. Finally, the stimulus sets of studies A1 and B differ in their third dimension, most likely because of a practical particularity of the experimental protocol: the sounds of set A1 were first loudness-equalized, unlike those of set B. The correlation scores between dimensions of the motor sound stimulus sets and the best-fitting acoustic features (see Appendix D) are presented in Table 3.
 ).
).Dimension 1: Harmonic Emergence (HNR)
For all three stimulus sets, several acoustic features correlate highly with this shared dimension, but they were of quite different types, and not all of them were significant. Furthermore, only one feature correlated well with this first dimension for the three stimulus sets: the Harmonic-to-Noise Ratio (HNR). Perceptual differences in the sounds along this dimension are related to the amount of harmonic (or pseudoharmonic) energy in the signal. The HNR linear regressions with the first dimension of every motor stimulus set are shown in Figures 3(a) to 3(c). The other features that correlated highly with this dimension were usually spectral envelope features. Actually, those high correlation scores are consequences of the HNR correlation. Indeed, the spectral envelopes of both parts of the sounds have quite different behaviors, and when the proportion of both parts is modified, the overall spectral aspect of the sound is also modified.
Dimension 2: Complex Brightness
For the three stimulus sets, when listening to the sounds along this scale, brightness features, such as spectral centroid or sharpness, seem to explain the dimension. However, for the two stimulus sets in which the harmonic part is most prevalent, that is, sets A1 and B, the perception of brightness seems to depend on the harmonic proportion. Indeed, the brightness perception of a predominantly noisy sound is not the same as that of a predominantly harmonic sound, all the more because both parts have quite different spectral behaviors: the energy of the harmonic part is quite concentrated in the low frequencies for this type of sounds. It is thus essential to take into account both the harmonic and noise parts in the brightness estimation. That is, the reason why multidimensional linear regression theory (see P. Legendre and L. Legendre [22]) is applied in order to characterize that dimension with a unique feature depending on the brightnesses of both parts. Therefore, for each of the three stimulus sets, a linear combination of 3 components is found to be significantly correlated: Complex brightness =  , where
, where  is the Perceptual Spectral Centroid of the harmonic part,
is the Perceptual Spectral Centroid of the harmonic part,  is that of the noise part, and
is that of the noise part, and  is the overall Perceptual Spectral Spread (see Appendix D). Both harmonic and noise parts were separated with the method and Matlab code taken from Ellis [26]. The linear regressions of the obtained "complex brightness'' with the second dimensions of the motor metacategory are shown in Figures 4(a) to 4(c). However, no common combination was found to be correlated for every stimulus set. Table 4 shows the coefficients of this "Complex brightness" for each stimulus set.
is the overall Perceptual Spectral Spread (see Appendix D). Both harmonic and noise parts were separated with the method and Matlab code taken from Ellis [26]. The linear regressions of the obtained "complex brightness'' with the second dimensions of the motor metacategory are shown in Figures 4(a) to 4(c). However, no common combination was found to be correlated for every stimulus set. Table 4 shows the coefficients of this "Complex brightness" for each stimulus set.
Dimension 3:
-
Study A1.
This dimension seems to be well correlated with the Perceptual Spectral Spread—PSS (see Appendix D) calculated with logarithmic scales for both magnitude (level) and frequency. The linear regression of this feature with the third dimension of the perceptual space of this study is shown in Figure 5.
-
Study B.
Unlike study A, the sounds were not initially loudness-equalized in study B. Quite logically, the last dimension of this MDS analysis result is found to be significantly correlated with Loudness (see Appendix D). The linear regression between Loudness and the third dimension of the study B perceptual space is shown in Figure 6.
Loudness is a perceptually strong characteristic that can easily prevent slight variations of other features from emerging. Moreover, the fact that no third perceptual dimension was obtained for stimulus set A2 can be related to the predominance of the noisy part, which can mask some variations of other features. On the contrary, when the sounds are loudness-equalized and when the harmonic part is not entirely masked by the noise, such as in stimulus set A1, a third perceptual dimension (PSS, Perceptual Spectral Spread) seems to emerge and matches that of the perceptual space of (pseudo-)harmonic instrument-like sounds (see Section 4.1.2, Dimension 3). For these reasons, we were not able to unify this third dimension along the three corpora (A1, A2 and B).
4.1.3. Instrument-Like Category
This sound category corresponds to the stimulus set of study C. Its MDS analysis resulted in a 3-dimensional perceptual space presented in Section 2.2.3. According to the correlation scores in Table 5, those 3 dimensions are related to 3 different acoustic features presented in the following:
 ).
).Dimension 1: Roughness—Study C
This dimension seems to discriminate the monophonic from the polyphonic sounds. When listening to the sounds along this scale, one goes from perfectly harmonic tones to successively pseudoharmonic tones (tones with inharmonicity relationships between their partials) and polyphonic sounds (with several tones). Consistently, roughness correlates significantly with this dimension (see Appendix D). The linear regression of roughness onto the first dimension is shown in Figure 7.
Dimension 2: Perceptual Spectral Centroid (PSC): Simple Brightness—Study C
When listening to the sounds along this scale, the relation to the brightness of the sounds seems quiet obvious. This brightness is well quantified by the spectral centroid all the more when a perceptual model is used. Consistently, the Perceptual Spectral Centroid gives the best correlation score (see Appendix D). We call it Simple brightness because it can be formally seen as the degenerated form of the Complex brightness defined in the previous section, when harmonic and noise parts of the signal are not separated. The PSC linear regression with the second dimension is shown in Figure 8.
Dimension 3: Perceptual Spectral Spread (PSS)—Study C
This dimension is the one whose interpretation is the most difficult just by listening to the sounds along the scale. However, it could be associated with their "richness." It correlates quite well with the Perceptual Spectral Spread (see Appendix D). The linear regression of PSS onto the third dimension is shown in Figure 9.
4.1.4. Impact Category
This sound category corresponds to the stimulus set of study D. Its MDS analysis resulted in a 3-dimensional perceptual space presented in Section 2.4. According to the correlation scores in Table 6, those 3 dimensions are related to 3 different acoustic features presented.
 ).
).Dimension 1: Perceptual Spectral Centroid (PSC): Simple Brightness—Study D
The feature that best suits this dimension is the Perceptual Spectral Centroid (PSC) that includes a hearing model (see Appendix D). Indeed, this dimension describes the sounds' brightness. We call it Simple brightness for the same reasons presented in Section 4.1.2, regarding the second dimension of the instrument-like category. The linear regression between the PSC feature and the first perceptual dimension is shown in Figure 10. However, it is noticeable that there is a categorization phenomenon along this dimension, as the sounds labeled 9, 11, and 12 are much lower on that dimension than the other ones. This phenomenon comes from the MDS analysis results and is not only related to the tested features. Nonetheless, it tends to improve the correlation score.
Dimension 2: Cleanness Indicator—Study D
It seems, when listening to the sounds along this scale, that this dimension is linked with the cleanness of the sounds. More precisely, it discriminates sounds containing only one impulse such as sounds 1, 2, and 3, from those in which one or more impulses follow the main one (rattle, bounce, etc.), such as sounds 10, 8, and 7. The acoustic feature (Cleanness indicator) that best suits this dimension is an estimator of the short-term loudness variability of the sounds (see Appendix D). This linear regression of the Cleanness indicator onto the second dimension is shown in Figure 11.
Dimension 3: Sound Level—Study D
The RMS value is correlated with this dimension. Indeed, the dimension seems to be somehow related to pulse amplitude. The linear regression of this feature onto the perceptual dimension is shown in Figure 12.
4.1.5. Discussion
Looking for regularities and singularities among the 3 important categories of environmental sounds derived from the first part of this study, we finally identified the following.
-
(i)
One feature, Brightness, that is preponderant for the description of all sound categories (i.e., 1 dimension of the 5 perceptual spaces). This feature is actually a combination of different spectral envelope features: the perceptual spectral centroid of both harmonic and noise parts of the signal (
 and
and 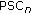 )—or perceptual spectral centroid of the whole signal (PSC)—and perceptual spectral spread (PSS). And no unique combination has been found to describe uniformly this dimension. So this feature still remains a generic notion of brightness and cannot be transformed into a real metric for quantifying this dimension.
)—or perceptual spectral centroid of the whole signal (PSC)—and perceptual spectral spread (PSS). And no unique combination has been found to describe uniformly this dimension. So this feature still remains a generic notion of brightness and cannot be transformed into a real metric for quantifying this dimension. -
(ii)
One or two features, in each category, that are related to specificities of the corresponding sounds:
-
(a)
motor sound perception is largely characterized by the mixture of two highly discriminable parts, in terms of either energy or spectral content;
-
(b)
instrument-like sounds present timbre features that have been found previously for musical sounds (essentially, roughness);
-
(c)
an important part of the perceptual discriminability of impact sounds is related to a temporal behavior feature, describing the sounds' cleanness.
-
(a)
4.2. Categorical Level: Building an Automatic Classifier
Now that we have identified the intercategory particularities, we must address the development of a predictive tool able to automatically classify the sounds on the basis of a perceptually validated corpus. In other words, the aim here is to use the results presented in Section 4.1 as relevant cues in order to find a limited number of acoustic features that would be efficient for the implementation of an automatic perceptual classifier.
4.2.1. Specificities of the Categories
Before considering the implementation of such a tool, it is essential to identify which features are used when listening to the sounds in order to discriminate the three categories. As partially concluded in Section 4.1.4, we can assume that:
-
(i)
impact sounds differ from the other ones in their temporal structure: they are quite short because they are damped, while the other sounds are as long as desired because they are sustained;
-
(ii)
instrument-like sounds differ from the other ones in their spectral structure: their spectrum energy is usually localized in the middle frequencies and their spread is quite low, because they are harmonic sounds whose degree of spectral envelope decrease is high. To the contrary, the spectrum energy of the other sounds is localized in much lower frequencies with a much higher spread and a lower degree of spectral envelope decrease.
Thus, it seems obvious that the cue that discriminates motor sounds from impact sounds, for instance, is very different from the one that discriminates motor sounds from instrument-like sounds. As a consequence, it is quite certain that a unique feature will not be enough to describe the categories, and it is more likely that we will have to use a pair of temporal and spectral features.
According to these preliminary observations, a large set of temporal/spectral feature pairs could be used in order to discriminate the category to which a given sound belongs. Spectral and temporal features that seem to be good candidates for dealing with this problem are listed below. Their terminology and computing techniques are taken from Peeters [15]:
-
(i)
temporal features: Log-Attack-Time (LAT), Temporal Increase (TI), Temporal Decrease (TD), Temporal Centroid (TC), Effective Duration (ED), Energy Modulation Frequency (EMF), and Energy Modulation Amplitude (EMA);
-
(ii)
spectral features: mean component of Spectral Centroid (SC), Spectral Spread (SSp), Spectral Skewness (SSk), Spectral Kurtosis (SK), Spectral Slope (SSl), Spectral Decrease (SD), Spectral RollOff (SR), and Spectal Variation (SV).
4.2.2. Classification Modeling Tool: The Multinomial Logistic Regression
Now that we have identified the feature combinations that are likely to discriminate the three sound categories, we need a regression modeling tool able to predict the values of a qualitative and polytomous dependent variable  (i.e., the sound category) by a combination of quantitative independent variables
(i.e., the sound category) by a combination of quantitative independent variables  (i.e., acoustic features). This tool is multinomial logistic regression (see P. Legendre and L. Legendre [22] and Woodcock [27]). In its basic definition, logistic regression is used to discriminate only two different attributes (or values) of a binary-dependent variable
(i.e., acoustic features). This tool is multinomial logistic regression (see P. Legendre and L. Legendre [22] and Woodcock [27]). In its basic definition, logistic regression is used to discriminate only two different attributes (or values) of a binary-dependent variable  (with values 0 and 1). With the probability notation
(with values 0 and 1). With the probability notation  of the event where the
of the event where the  variable has the value 1, given the
variable has the value 1, given the  value of the
value of the  set of variables, both event probabilities are related to each other by
set of variables, both event probabilities are related to each other by

A logistic regression tool models the  probability by a logistic function, formulated in (2). This function, which exhibits a sigmoid curve ("S-shaped" curve), is defined as the cumulative distribution function of a logistic probability distribution (similar to the normal distribution).
probability by a logistic function, formulated in (2). This function, which exhibits a sigmoid curve ("S-shaped" curve), is defined as the cumulative distribution function of a logistic probability distribution (similar to the normal distribution).

where  is a linear combination of the values of
is a linear combination of the values of  :
: 
Its inverse function, the "logit" function, corresponds to the natural logarithm of the odds' ratio in

When the dependent variable  corresponds to a polytomous nominal response (i.e., that has more than two different unordered values), the generalized logit models are used. In our case, the dependent variable
corresponds to a polytomous nominal response (i.e., that has more than two different unordered values), the generalized logit models are used. In our case, the dependent variable  corresponds to a 3-valued response: "0'' for impact, "1'' for motor, and "2'' for instrument-like. With the notation
corresponds to a 3-valued response: "0'' for impact, "1'' for motor, and "2'' for instrument-like. With the notation  , the multinomial logistic regression consists in modeling the relationship between the set of independent variables
, the multinomial logistic regression consists in modeling the relationship between the set of independent variables  and the generalized logits,
and the generalized logits,  and
and  . The model assumes a linear relationship for each logit as in
. The model assumes a linear relationship for each logit as in

The regression tool searches iteratively for the best-fitting solution ( coefficients) using the Newton-Raphson method and maximum log-likelihood as a convergence criterion. The predicted probabilities are then given by
coefficients) using the Newton-Raphson method and maximum log-likelihood as a convergence criterion. The predicted probabilities are then given by

where  and
and  .
.
4.2.3. Model Selection
This tool is applied to the perceptually validated sound corpus established at the end of Section 3, in order to predict the belonging of a sound to one of the 3 identified categories. This corpus is large enough (207 sounds) to make the results of such a procedure relevant. According to the set of acoustic features selected in Section 4.2.1, we can compute a classification model for each pair of spectral/temporal features. The best model's selection is made on the basis of their respective log-likelihoods. The log-likelihood LL is a statistical feature that corresponds to the sum of each natural logarithm of the predicted probability  that a sound belongs to its supposed category, as described in
that a sound belongs to its supposed category, as described in

However, the log-likelihood value depends on the number of elements within the stimulus set, and having the same value with stimulus sets of different size is not as relevant. A way to take this into account is to calculate a likelihood ratio that quantifies the gain in correct prediction of the model compared to the "intercept only" model, where only the β0 constant coefficients are used (This means that the "intercept only" model will give the same probabilities whatever the data. In the present case, it will give a 99/207 = 0.48 probability of belonging to the motor category, a 49/207 = 0.24 probability of belonging to the instrument-like category, and a 59/207 = 0.28 probability of belonging to the impact category). The likelihood ratio feature LR is obtained with the relation defined in

where  is the "intercept only" model log-likelihood. This statistical feature allows us to compare the effectiveness of each model (i.e., each feature pair) in predicting the category to which a given sound belongs. The higher the LL and LR values are, the more efficient the model is (see P. Legendre and L. Legendre [22]). The LR value for each feature pair is shown in Table 7, where we can see that the SSp/ED model seems to best suit the data.
is the "intercept only" model log-likelihood. This statistical feature allows us to compare the effectiveness of each model (i.e., each feature pair) in predicting the category to which a given sound belongs. The higher the LL and LR values are, the more efficient the model is (see P. Legendre and L. Legendre [22]). The LR value for each feature pair is shown in Table 7, where we can see that the SSp/ED model seems to best suit the data.
4.2.4. Model Validation
In order to test the robustness of the selected model using SSp and ED features (see Section 4.2.3), a usual method consists of:
-
(i)
reestimating the model on a randomly selected reduced part of the stimulus set, 70% of it for instance (144 sounds with respect to the distribution in the 3 categories),
-
(ii)
calculating the estimated probabilities on the remaining 30% (63 sounds),
-
(iii)
evaluating the error percentage. (We consider as an error the case of a sound for which the probability of belonging to its supposed category is smaller than one of the two other probabilities. This means that if the model has to choose the category to which the sound belongs, it will choose a wrong one.)
This procedure was performed 100 times with a different random selection of sounds each time. This method tests whether the effectiveness of the model prediction will hold when applied to other sounds than those used to estimate its coefficients.
When estimated on the whole 207-sound stimulus set, the best-fitting model makes 7 errors, which corresponds to an error percentage of 3.3%. Over the 100 times, we performed the procedure explained above, and we obtained the results presented in Table 8, calculated on the recall number (total number minus number of errors) of every remaining 30% selection of the stimulus set. Note that the mean recall percentage (95.9%) is rather high, not even much smaller than when obtained on the whole stimulus set (96.7%), which proves the model's adequacy for this dataset.
 ,
,  ).
). ,
,  ).
). ,
,  ).
). ,
,  ).
). .
.4.2.5. Discussion
The selected model tested on a 207-sound stimulus set (augmented corpus established in Experiment  , Section 3.2) gives significant stable results in terms of automatic classification with only around 4% mean error in the prediction, with only 2 predicting acoustic features. This is a rather encouraging result, even if this tool is built with only 3 main sound categories of quite different kinds (motor, instrument-like, and impact). It could be extended to other categories in order to cover a larger scope of environmental sounds.
, Section 3.2) gives significant stable results in terms of automatic classification with only around 4% mean error in the prediction, with only 2 predicting acoustic features. This is a rather encouraging result, even if this tool is built with only 3 main sound categories of quite different kinds (motor, instrument-like, and impact). It could be extended to other categories in order to cover a larger scope of environmental sounds.
Other automatic classification methods exist that are much more complex and that use much more input information about the sounds. But considering the significant results of this relatively simple method, exploring these algorithms further is quite pointless. However, with more than 3 categories, these methods may outperform the one presented here and could therefore be useful for efficient automatic classification.
From a larger point of view, other classification approaches also exist that are less time consuming with regard to the available data needed for performing them: they usually consist in defining sound classes, collecting training examples for each class, computing a large set of spectral and temporal features on sounds, and letting a machine learning method pick features that are efficient in discriminating the classes. But, the main difference between this approach and the one proposed in the present paper relies on the fact that in the former, the classes are arbitrarily defined (or at least, are the result of a single expert's analysis), whereas in the present paper the classes are deduced from an experimental procedure, which is more time consuming but allows them to be considered as perceptually relevant. This is one of the original contributions of this study with regard to traditional methods based on a priori sound categories and powerful learning techniques (e.g., like the ones used in Music Information Retrieval research (http://www.ismir.net/)).
4.3. Summary
We built a 2-level description structure of environmental sounds that consists of:
-
(i)
a categorical level that considers the different sound categories corresponding to particular sound production mechanisms,
-
(ii)
a continuous level that defines, within each of these categories, the perceptual space of the sounds representing the perceptual dissimilarity between two sounds of the same kind.
This description is associated with automatic processing of acoustic features. When considering a new sound of one of these kinds, this processing allows: (i) the identification of the sound category to which it belongs, with regard to the probabilities estimated by the logistic regression model and (ii) its correct placement along several perceptual dimensions.
5. Conclusion
This work sought to extend timbre description principles, usually used for musical sounds, to environmental sounds and to apply them in a more systematic manner to this class of sounds. It is based on a first step of reexamination and comparison of four primary studies mainly dealing with industrial (car and machine) sounds. An inventory of their respective contexts, motivations, procedures, and results gave us input data consisting of 5 coherent stimulus sets with their associated low-dimensional perceptual spaces. It also allowed us to intuit some regularities and singularities among the different kinds of sounds under consideration. Within the restricted scope of these 5 stimulus sets, a 2-part experimental approach revealed 3 metacategories (motor, instrument-like, and impact) and precisely defined them on a larger scale by extending the contents of each one. This categorical description structure is also coherent with the categories of product sounds that Özcan and van Egmond [23] found. Finally, a modeling approach was designed to describe more precisely the intuited regularities and singularities of these 3 categories. This includes comparing the initial perceptual spaces by means of systematically correlated acoustic features, which can be summarized by two important facts.
-
(i)
One feature is preponderant for the description of all sound categories, that is, brightness usually based on spectral envelope features. Therefore, this perceptual feature appears to describe musical sounds as well as environmental sounds.
-
(ii)
One or two features, in each category, are related to a specificity of the corresponding sounds:
-
(a)
motor sound perception is largely characterized by the mixture of two highly discriminable parts (harmonic and noise), in terms of either energy or spectral content;
-
(b)
instrument-like sounds present timbre features, originally derived for the description of musical sounds;
-
(c)
an important part of the perceptual discriminability of impact sounds is related to a temporal behavior feature, describing the sounds' cleanness.
-
(a)
This modeling approach also includes the building of a predictive tool based on logistic regression able to classify automatically and rather efficiently (with only 4% mean error) this metastructure with regard to the 3 categories under consideration.
Note that contrary to musical timbre, for which attack time is an important cue of the perceptual space, the studies revealed no temporal features corresponding to the two first categories. This may be mainly due to the quasistationary nature of these sounds. Nonetheless, a temporal parameter associated with a spectral one appeared to be fairly efficient in automatically discriminating impulsive environmental sounds (car door closing) from nonimpulsive ones.
However, according to Özcan and van Egmond [23], other major sound categories, such as liquid or cyclic sounds, exist and need a definition as well, and their main perceptual features must be investigated. Furthermore, they focused their study on domestic "product sounds,'' while we were more interested in industrial sounds. Considering environmental sounds in a more general sense may again reveal other categories that would also need to be taken into consideration when building an overall environmental sound description structure, in terms of either definition or automatic description.
From an application point of view, the relevant acoustic features obtained for the three categories of sounds will allow us to conceive of perceptually relevant organization structures of large environmental sound collections and to propose retrieval systems using an intuitive query process by searching for sounds that are similar to a target sound in that kind of database. The search will be based on similarity metrics computed from the acoustic features, and stored with the sounds in the database as proposed by previous studies for musical sounds (Blum et al. [28], Misdariis et al. [29], Qi et al. [30]). From a larger perspective, these results should also contribute to the elaboration of a functional Computer-Aided Sound Design framework as they will help users to describe, associate, compare, share, and finally manipulate sounds that can be considered as prototypes or initial ideas of concepts that the designer has in mind and tries to materialize in the framework of a specific project.
Appendices
A. Multidimensional Scaling (MDS) Analysis' Principles
A.1. MDS Models
MDS techniques represent the dissimilarity data by distances in a geometrical space. The simplest model represents the dissimilarity  between two sounds
between two sounds  and
and  , averaged across the participants' ratings, by an Euclidean distance in a geometrical space with
, averaged across the participants' ratings, by an Euclidean distance in a geometrical space with  dimensions:
dimensions:

where  is the coordinate of sound
is the coordinate of sound  on the
on the  th dimension.
th dimension.
In this model, the space is rotationally invariant, which means that rotating its axes will not intrinsically change the space structure as long as they remain orthogonal.
The increasing sophistication of MDS techniques has led to a refinement of the initial model. This model, called INDSCAL (Individual Differences Scaling; Carroll and Chang [31]), also considers the possibility that subjects weight the dimensions differently. It represents the dissimilarity  between two sounds
between two sounds  and
and  , for each subject s by
, for each subject s by

where  is the weight given by subject
is the weight given by subject  to dimension
to dimension  .
.
Another refinement is proposed by the CLASCAL model (Latent Class Approach) (Winsberg and De Soete [32]). The dissimilarities are modeled as distances in an extended Euclidean space of R dimensions. Thus, the CLASCAL model postulates common dimensions shared by all stimuli, attributes particular to each stimulus (so-called specificities), and latent classes of subjects. Specificities account for the possibility that a sound may possess some unique feature that other sounds of the set do not share. Latent classes have different saliences or weights for each of the common dimensions and for the whole set of specificities. For latent class  , the distance between two sounds
, the distance between two sounds  and
and  within the perceptual space is thus computed according to:
within the perceptual space is thus computed according to:

In (A.3),  is the distance between sound
is the distance between sound  and sound
and sound  ,
,  is the index of the
is the index of the  latent classes,
latent classes,  is the coordinate of sound
is the coordinate of sound  along the
along the  th dimension,
th dimension,  is the weight of dimension
is the weight of dimension  for class
for class  ,
,  is the total number of dimensions,
is the total number of dimensions,  is the weight of the specificities for class
is the weight of the specificities for class  , and
, and  is the specificity of sound
is the specificity of sound  .
.
The class structure is latent: there is no a priori assumption concerning the latent class to which a given subject belongs. The CLASCAL analysis yields a spatial representation of the  stimuli on the
stimuli on the  dimensions, with the specificity of each stimulus, the probability that each subject belongs to each latent class, and the weights or saliences of each salient perceptual dimension for each class.
dimensions, with the specificity of each stimulus, the probability that each subject belongs to each latent class, and the weights or saliences of each salient perceptual dimension for each class.
Moreover, in the INDSCAL and CLASCAL models, the presence of dimension weights that differ between subjects or classes of subjects removes the rotational invariance of the obtained spaces, because the dimensions are fixed by the presence of those weights. As a consequence, it is assumed in both models that the dimensions of the space are perceptually meaningful.
B. Complementary Data and Initial Results Related to the Four Primary Studies
B.1. Data Related to Study A1 (Table 9 and Figure 13)
-
(i)
RAPmv-A: A-weighted harmonic-to-noise ratio. Both harmonic and noise parts were separated using additive analysis/synthesis (see Rodet [33], for more detail on the separation technique). The feature is the ratio of their levels expressed in dB(A).
-
(ii)
CGg-ERB: ERB Spectral centroid. The frequency dimension is represented in ERB-rate (distance in terms of Equivalent-Rectangular Bandwidth (ERB) filters; see Patterson et al. [34] and Slaney [35]).
-
(iii)
Dec: Harmonic spectral decrease. This feature is related to the shape of the spectral envelope computed from the harmonic components of the signal. In the present case, this feature is computed on the bandwidth of the spectrum, but represents the relative decrease in the envelope of the harmonic spectrum only between 266?Hz and 2300?Hz.
B.2. Data Related to Study A2 (Table 10 and Figure 14)
-
(i)
rad - 2N/0.5N: 2N and 0.5N harmonic ratios, where N is deduced from the RPM value of engine rotation.
-
(ii)
CGg-C: Spectral centroid, with linear frequency using C weighting.
B.3. Data Related to Study B (Table 11 and Figure 15)
-
(i)
NHR-A: Feature corresponding to the relative balance of the harmonic (motor) and noise (air turbulence) components. The best correlation is obtained with the A-weighted version of this parameter.
-
(ii)
 -B: B-weighted spectral centroid of the noise component. For this dimension, the emergence of a spectral pitch led us to consider the spectral centroid (SC). More precisely, we compute the SC of each of the two parts of the sound: the noise component (
-B: B-weighted spectral centroid of the noise component. For this dimension, the emergence of a spectral pitch led us to consider the spectral centroid (SC). More precisely, we compute the SC of each of the two parts of the sound: the noise component (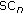 ) and the harmonic component (
) and the harmonic component ( ). The best correlation with Dimension 2 is obtained for
). The best correlation with Dimension 2 is obtained for  using B-weighting.
using B-weighting. -
(iii)
N: Loudness. Indeed, even though the selected sounds are in the same range of loudness, they were not equalized in loudness.
B.4. Data Related to Study C (Table 12 and Figure 16)
-
(i)
Roughness: feature modeled by the amplitude modulation rate of the temporal envelope (expressed in asper) and related to the sensation of auditory roughness.
-
(ii)
Spectral centroid: feature describing the spectral distribution of the energy of the sound, computed from a frequency decomposition on the ERB scale (Marozeau et al. [13]). It has been identified as corresponding to the sensation of "brightness.''
-
(iii)
Spectral deviation: feature related to the fine structure of the spectral envelope. It is computed based on the smoothness of the outputs of the filter-bank (Marozeau et al. [13]).
B.5. Data Related to Study D (Table 13 and Figure 17)
-
(i)
Spectral centroid: feature describing the spectral distribution of the energy of the sound.
-
(ii)
Sharpness: feature defined by Aures [17], similar to spectral centroid with perceptual modeling.
-
(iii)
Cleanness indicator: indicator that is derived from the temporal loudness calculation according to Zwicker's model [18]. The algorithm takes into account temporal integration and temporal masking. The proposed indicator is based on the temporal evolution of the curve.
C. Illustration of the Experimental Graphical User Interfaces Used in Experiments 1 and 2
See Figures 18 and 19 for screenshots of Experiments  and
and  .
.
D. Details of Acoustic Features Calculation
D.1. RMS Value
The estimation of the RMS (Root-Mean-Square) value of the signal is frame-based and is calculated every 60 ms with a Blackman window. The feature is the mean value over time.
D.2. Loudness
Loudness is the intensive attribute of human hearing. It thus describes the subjective aspect of the intensity of a signal by considering masking effects that occur over the whole spectrum and the filtering steps of the hearing path. The loudness model used is the ISO 532-B model from Zwicker and Fastl [24].
D.3. Harmonic Emergence Feature
This feature is a Harmonic-to-Noise ratio, designed to convey the relative amounts of harmonic (or pseudoharmonic) energy and noise energy in the signal. It is based on the Pm2 partial extraction method (see Bogaards et al. [36]). Once both harmonic and noise parts of the signal are extracted, the feature simply consists of the ratio of their respective loudnesses  and
and  as formalized in
as formalized in

D.4. Spectral Centroid
The spectral centroid is a weighted mean frequency of the spectrum of the signal. The calculation of this feature can be more or less complex. Its definition is quite similar to Zwicker and Fastl's [24] sharpness feature. It uses a gammatone filterbank (from Auditory Toolbox, Slaney [16]) that is based on the ERB-rate scale  (see Marozeau et al. [13] for more details). The resulting feature is the Perceptual Spectral Centroid as defined in
(see Marozeau et al. [13] for more details). The resulting feature is the Perceptual Spectral Centroid as defined in

where  is the specific loudness in each channel (obtained by each gammatone filter) and
is the specific loudness in each channel (obtained by each gammatone filter) and  is the corresponding center frequency.
is the corresponding center frequency.
D.5. Spectral Spread
The spectral spread describes how the spectrum is spread around its mean value, that is, the spectral centroid defined above. The associated perceptual feature uses the same perceptual modeling as the PSC feature, thus giving the Perceptual Spectral Spread PSS, as defined in

D.6. Complex Brightness
This feature estimates the brightness sensation of a sound that combines a noisy and a harmonic part. It simply corresponds to the linear combination of the PSC values of both noisy and harmonic parts (resp.,  and
and  ) and the PSS value of the whole signal, as defined in
) and the PSS value of the whole signal, as defined in

where  ,
,  , and
, and  are linear coefficients.
are linear coefficients.
D.7. Roughness
Roughness is a feature that quantifies the perceived modulation or graininess of a sound. When inharmonicity is strong, amplitude modulations can generate beating in some cases. When the beating becomes fast enough so that the modulations are no longer discriminated by the human ear, they seem to give a rough aspect to the sound. This roughness feature (also defined in Grey [10]) mainly consists in estimating a modulation index at the output of every auditory filter, which is called the partial roughness. The overall roughness is the sum of all the partial roughnesses. From each auditory filter output, the modulation frequency  and the modulation depth
and the modulation depth  are estimated with a temporal envelope calculation. The partial roughness is proportional to the product of the modulation frequency and the depth
are estimated with a temporal envelope calculation. The partial roughness is proportional to the product of the modulation frequency and the depth  . The roughness
. The roughness  is then calculated as the sum of the
is then calculated as the sum of the  ,
,

where  is the proportionality coefficient.
is the proportionality coefficient.
D.8. Cleanness Indicator
This feature represents the short-term variations in the loudness of the signal. These variations, which usually occur between 20 and 100 Hz, are slow enough to be heard as a temporal phenomenon, but they are too fast to be heard as separate sound events (e.g., bounces, rattles, etc.). The feature corresponds to the amplitude of the spectrum of the instantaneous loudness  , which is estimated every 3.3 msec., within this frequency band
, which is estimated every 3.3 msec., within this frequency band

where FFT256 is the 256-point Fast Fourier Transform.
References
Vanderveer NJ: Ecological acoustics: human perception of environmental sounds, unpublished doctoral dissertation. Cornell University; 1979.
Susini P, McAdams S, Winsberg S: Caractérisation perceptive des bruits de véhicules. Proceedings of 4ème Congrès français d'acoustique, 1997, Marseille, France
Susini P, McAdams S, Winsberg S: Perceptual characterisation of vehicules noises. EEA Symposium: Psychoacoustic in Industry and Universities, 1997, Eindhoven, The Netherlands
Susini P, McAdams S, Winsberg S: A multidimensional technique for sound quality assessment. Acustica 1999, 85(5):650-656.
McAdams S, Susini P, Misdariis N, Winsberg S: Multidimensional characterisation of perceptual and preference judgements of vehicle and environmental noises. Proceedings of Euronoise Conference, 1998, Munich, Germany
Susini P, McAdams S, Winsberg S, Perry I, Vieillard S, Rodet X: Characterizing the sound quality of air-conditioning noise. Applied Acoustics 2004, 65(8):763-790. 10.1016/j.apacoust.2004.02.003
Lemaitre G, Susini P, Winsberg S, McAdams S, Letinturier B: The sound quality of car horns: a psychoacoustical study of timbre. Acta Acustica United with Acustica 2007, 93(3):457-468.
Lemaitre G, Susini P, Winsberg S, McAdams S, Letinturier B: The sound quality of car horns: designing new representative sounds. Acta Acustica United with Acustica 2009, 95(2):356-372. 10.3813/AAA.918158
Parizet E, Guyader E, Nosulenko V: Analysis of car door closing sound quality. Applied Acoustics 2008, 69(1):12-22. 10.1016/j.apacoust.2006.09.004
Grey JM: Multidimensional perceptual scaling of musical timbres. The Journal of the Acoustical Society of America 1977, 61(5):1270-1277. 10.1121/1.381428
Krumhansl CL: Why is musical timbre so hard to understand? In Structure and Perception of Electroacoustic Sound and Music. Edited by: Nielzen S, Olsson O. Elsevier, Amsterdam, The Netherlands; 1989:43-53. (Excerpta Medica 846)
McAdams S, Winsberg S, Donnadieu S, de Soete G, Krimphoff J: Perceptual scaling of synthesized musical timbres: common dimensions, specificities, and latent subject classes. Psychological Research 1995, 58(3):177-192. 10.1007/BF00419633
Marozeau J, de Cheveigne A, McAdams S, Winsberg S: The dependency of timbre on fundamental frequency. The Journal of the Acoustical Society of America 2003, 114(5):2946-2957. 10.1121/1.1618239
McAdams S: Recognition of auditory sound sources and events. In Thinking in Sound: The Cognitive Psychology of Human Audition. Edited by: McAdams S, Bigand E. Oxford University Press, Oxford, UK; 1993.
Peeters G: A large set of audio features for sound description (similarity and classification). CUIDADO project Ircam technical report 2004. http://www.ircam.fr/anasyn/peeters/ARTICLES/Peeters_2003_cuidadoaudiofeatures.pdf
Slaney M: Auditory Toolbox, version 2. Tech. Rep. 1998-010, Interval Research Corporation; 1998.http://cobweb.ecn.purdue.edu/~malcolm/interval/1998-010/
Aures W: Der sensorische Wohlklang als Funktion psychoakustischer Empfindungsgrößssen. Acustica 1985, 58(5):282-290.
Zwicker E: Procedure for calculating loudnesss of temporally variable sounds. The Journal of the Acoustical Society of America 1977, 62(3):675-682. 10.1121/1.381580
McAdams S: Recognition of auditory sources and events. In Thinking in Sound: The Cognitive Psychology of Human Audition. Edited by: McAdams S, Bigand E. Oxford University Press, Oxford, UK; 1993:146-198.
Rosch E: Principles of categorization. In Cognition and Categorization. Lawrence Erlbaum Associates; 1978:27-48.
Kruskal JB, Wish M: Multidimensional Scaling, Sage University Paper Series on Quantitative Applications in the Social Sciences 07-011. Sage Publications, Beverly Hills, Calif, USA; 1978.
Legendre P, Legendre L: Numerical Ecology. Development in Environmental Modelling. 2nd edition. Elsevier, Amsterdam, The Netherlands; 1998.
Özcan E, van Egmond R: Memory for product sounds: the effect of sound and label type. Acta Psychologica 2007, 126(3):196-215. 10.1016/j.actpsy.2006.11.008
Zwicker E, Fastl H: Psychoacoustics: Facts and Models. Springer, New York, NY, USA; 1990.
Smith BK: PsiExp: an environment for psychoacoustic experimentation using the IRCAM musical workstation. In Society for Music Perception and Cognition Conference. University of Berkeley, Berkeley, Calif, USA; 1995.
Ellis DPW: Sinewave and Sinusoid+Noise Analysis/Synthesis in Matlab. 2003, http://labrosa.ee.columbia.edu/matlab/sinemodel/
Woodcock S: MATLAB econometrics toolbox. 2003, http://www.sfu.ca/~swoodcoc/software/software.html
Blum T, Keislar D, Wheaton J, Wold E: Audio database with content-based retrieval. Annual Review of Physiology 1995, 61: 457-476.
Misdariis N, Smith BK, Pressnitzer D, Susini P, McAdams S: Validation of a multidimensional distance model for perceptual dissimilarities among musical timbres. The Journal of the Acoustical Society of America 1998, 103(5):3005-3006.
Qi H, Hartono P, Suzuki K, Hashimoto S: Sound database retrieved by sound. Acoustical Science and Technology 2002, 23(6):293-300. 10.1250/ast.23.293
Carroll JD, Chang J-J: Analysis of individual differences in multidimensional scaling via an n-way generalization of "Eckart-Young" decomposition. Psychometrika 1970, 35(3):283-319. 10.1007/BF02310791
Winsberg S, De Soete G: A latent class approach to fitting the weighted Euclidean model, clascal. Psychometrika 1993, 58(2):315-330. 10.1007/BF02294578
Rodet X: The additive analysis-synthesis package. Ircam tutorial, http://recherche.ircam.fr/equipes/analyse-synthese/DOCUMENTATIONS/additive/index-e.html
Patterson RD, Robinson K, Holdsworth J, McKeown D, Zhang C, Allerhand M: Complex sounds and auditory images. In Auditory Physiology and Perception. , Oxford, UK; 1995:429-446.
Slaney M: An efficient implementation of the Patterson-Holdsworth auditory filter bank. Tech. Rep. 35, Apple Computer; 1993.
Bogaards N, Roebel A, Rodet X: Sound analysis and processing with AudioSculpt 2. Proceedings of International Computer Music Conference (ICMC '04), 2004, Miami, Fla, USA
Acknowledgment
Some of these results come from the SampleOrchestrator project funded by the French Agence Nationale de la Recherche (ANR): http://www.ircam.fr/306.html?&tx_ircamprojects_pi1%5BshowUid%5D=36&tx_ircamprojects_pi1%5BpType%5D=p&cHash=9859699b3d.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Misdariis, N., Minard, A., Susini, P. et al. Environmental Sound Perception: Metadescription and Modeling Based on Independent Primary Studies. J AUDIO SPEECH MUSIC PROC. 2010, 362013 (2010). https://doi.org/10.1155/2010/362013
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/362013

 83 matrix, if sound j was selected by a listener as prototype of a category that contains sound
83 matrix, if sound j was selected by a listener as prototype of a category that contains sound  , then cell
, then cell  is incremented (but not cell
is incremented (but not cell  ).
).

















 and
and 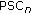 )—or perceptual spectral centroid of the whole signal (PSC)—and perceptual spectral spread (PSS). And no unique combination has been found to describe uniformly this dimension. So this feature still remains a generic notion of brightness and cannot be transformed into a real metric for quantifying this dimension.
)—or perceptual spectral centroid of the whole signal (PSC)—and perceptual spectral spread (PSS). And no unique combination has been found to describe uniformly this dimension. So this feature still remains a generic notion of brightness and cannot be transformed into a real metric for quantifying this dimension. -B: B-weighted spectral centroid of the noise component. For this dimension, the emergence of a spectral pitch led us to consider the spectral centroid (SC). More precisely, we compute the SC of each of the two parts of the sound: the noise component (
-B: B-weighted spectral centroid of the noise component. For this dimension, the emergence of a spectral pitch led us to consider the spectral centroid (SC). More precisely, we compute the SC of each of the two parts of the sound: the noise component (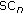 ) and the harmonic component (
) and the harmonic component ( ). The best correlation with Dimension 2 is obtained for
). The best correlation with Dimension 2 is obtained for  using B-weighting.
using B-weighting.