- Research Article
- Open access
- Published:
Towards an Intelligent Acoustic Front End for Automatic Speech Recognition: Built-in Speaker Normalization
EURASIP Journal on Audio, Speech, and Music Processing volume 2008, Article number: 148967 (2008)
Abstract
A proven method for achieving effective automatic speech recognition (ASR) due to speaker differences is to perform acoustic feature speaker normalization. More effective speaker normalization methods are needed which require limited computing resources for real-time performance. The most popular speaker normalization technique is vocal-tract length normalization (VTLN), despite the fact that it is computationally expensive. In this study, we propose a novel online VTLN algorithm entitled built-in speaker normalization (BISN), where normalization is performed on-the-fly within a newly proposed PMVDR acoustic front end. The novel algorithm aspect is that in conventional frontend processing with PMVDR and VTLN, two separating warping phases are needed; while in the proposed BISN method only one single speaker dependent warp is used to achieve both the PMVDR perceptual warp and VTLN warp simultaneously. This improved integration unifies the nonlinear warping performed in the front end and reduces simultaneously. This improved integration unifies the nonlinear warping performed in the front end and reduces computational requirements, thereby offering advantages for real-time ASR systems. Evaluations are performed for (i) an in-car extended digit recognition task, where an on-the-fly BISN implementation reduces the relative word error rate (WER) by 24%, and (ii) for a diverse noisy speech task (SPINE 2), where the relative WER improvement was 9%, both relative to the baseline speaker normalization method.
1. Introduction
Current speaker-independent automatic speech recognition (ASR) systems perform well in most of the real-world applications but the performance gap between speaker-dependent and speaker-independent settings is still significant. Although a reasonable amount of progress have occurred in recent years in the general ASR technology by exploiting more complex algorithms with the help of faster computing [1], little progress has been reported in the development of core speech processing algorithms. Many speech researchers would agree that there is still a significant potential in formulating an acoustic representation of the speech signal that will successfully maintain information needed for efficient speech recognition, especially in noise, while eliminating irrelevant speaker-dependent information [1]. The perceptual MVDR (PMVDR) coefficients have proven to be more effective than the MFCC front end on a number of tasks, especially in noisy environments [2, 3]. This paper introduces a new and computationally efficient speaker normalization algorithm within the PMVDR [2, 3] framework which we call built-in speaker normalization (BISN). BISN is computationally efficient and can be completely integrated into the front-end.
There are different ways to address speaker variability for automatic speech recognition. One approach is to normalize speaker variabilities in the feature space prior to employing an HMM acoustic recognizer framework. A number of effective algorithms have been developed to compensate for such variabilities due to speaker stress and emotion (see [4] for an overview). Probably, the most successful approach is the adaptive cepstral compensation (ACC) [5] which was shown to significantly reduce the impact of speaker variability for ASR. This approach uses a low-level voiced/transitional/unvoiced segmentation scheme followed by a source generator framework to compensate the MFCC cepstral feature sequence prior to ASR. More recent approaches have focused on reducing the impact of vocal-tract length differences in the spectral domain [6, 7].
Basic likelihood-based warp estimation was first introduced by Andreou et al. [8]. However, it was computationally cumbersome and required a substantial amount of speech from each speaker in order to estimate the best warp factor. Their basic motivation was to extract acoustic features that have reduced speaker dependency. In order to achieve this, they linearly warped the frequency axis. The degree of this linear warping is in fact a speaker-dependent factor and must be estimated for each speaker. For the estimation of the warp factor, they proposed a set of maximum likelihood-based procedures. Unfortunately, these procedures were computationally very expensive.
Lee and Rose [6, 7] proposed a set of speaker normalization procedures using maximum likelihood estimates of the best warp for each speaker. There was no attempt to recover the underlying vocal-tract shape. Instead, their motivation was to use an optimization criterion directly related to the one used in the recognizer. They revised the set of maximum likelihood estimation procedures proposed by Andreou [8] to estimate the warp factors for each speaker. These procedures are now widely known as vocal-tract length normalization (VTLN). The most popular way of estimating VTLN warps is to use likelihood-based estimation techniques [6, 7] in which a set of HMM models trained on a large population of speakers by placing 1 Gaussian per state is scored against warped features. Afterwards, incoming features are extracted using different VTLN warps, and the warp producing the maximum likelihood (given the HMMs and transcription) is used as the best VTLN warp for that speaker. VTLN is shown to be effective for a number of tasks but the computational load of determining the best warp for each speaker, especially at the time of recognition, is not tractable. They also proposed computationally more efficient variants of the VTLN based on the GMM modeling of each VTLN warp [6, 7]. However, these variants are less accurate due to the loss of temporal information (this stems from the use of GMMs in the modeling) buried in the speech signal. As a result, although a good method for offline simulations, classical VTLN is rarely used in practical systems where computational efficiency is of primary concern. Therefore, there is a need for achieving on-the-fly speaker normalization by introducing computationally more efficient algorithms.
Eide and Gish [9] proposed a waveform-based algorithm, in which they estimate the warping factors by using the average position of the third formant. Their idea is that the third formant is not affected as much as the first and second formants from the context and therefore more closely related to the speaker's vocal-tract length. By using the ratio of the average third-formant location for a particular speaker to the average third-formant location for a large population of speakers, they were able to determine reasonable normalization factors, which helped reduce interspeaker variations. Although this approach has the advantage of estimating the speaker-normalization warps directly from the speech signal, the difficulty of estimating the third formant reliably even for clean speech is apparent, as some speakers may not even have clear third-formant locations.
Acero [10] proposed a speaker-dependent bilinear transform (BLT) to account for interspeaker variations. In that study, an LPC-based front end is used with the FFT spectrum warped before the computation of the cepstral coefficients. A vector quantization distortion measure is computed to estimate the best BLT warp for each speaker. Substantial performance improvements were obtained with the LPC-based cepstral coefficients (LPCCs). The proposed BISN algorithm has some similarities with Acero's approach [10]. In both methods, a first-order all-pass system (or a BLT) is used to incorporate the perceptual scale into the feature extraction process. A fixed BLT warp factor,  is used to approximate Mel and Bark scales as needed. In order to reduce the speaker differences, a best BLT warp factor,
is used to approximate Mel and Bark scales as needed. In order to reduce the speaker differences, a best BLT warp factor,  is specifically estimated for each speaker, which in some sense, integrates perceptual BLT warp and speaker normalization BLT warp into a single speaker-dependent BLT warp factor. The procedure employed to estimate the best BLT warp factor for each speaker, on the other hand, has substantial differences. As mentioned above, Acero used a vector quantization distortion measure in order to estimate the best BLT warp factor for each speaker. Our approach in BISN is fundamentally different in the sense that each best BLT warp factor is estimated within the VTLN framework proposed by Lee and Rose [6, 7]. Moreover, several other algorithms are also integrated within the search process in order to reduce the computational load down to manageable levels for real-time implementations.
is specifically estimated for each speaker, which in some sense, integrates perceptual BLT warp and speaker normalization BLT warp into a single speaker-dependent BLT warp factor. The procedure employed to estimate the best BLT warp factor for each speaker, on the other hand, has substantial differences. As mentioned above, Acero used a vector quantization distortion measure in order to estimate the best BLT warp factor for each speaker. Our approach in BISN is fundamentally different in the sense that each best BLT warp factor is estimated within the VTLN framework proposed by Lee and Rose [6, 7]. Moreover, several other algorithms are also integrated within the search process in order to reduce the computational load down to manageable levels for real-time implementations.
The feasibility of bilinear and all-pass transforms (BLT, APT) has also been extensively studied by McDonough [11, 12]. In that study, the BLT is implemented in the cepstral domain. The best BLT parameters were estimated by a Gaussian mixture model (GMM) as the one maximizing the likelihood of the incoming data [11, 12]. The BISN approach is somehow related to this method, however relation is merely in the use of a BLT for speaker normalization. McDonough did not make any attempt to integrate perceptual warp and speaker normalization BLT warp into a single warp (which BISN does). Rather, he used cepstrum transformation matrices (which are derived from the BLT) on the final MFCC vectors to achieve the speaker normalization. This means that still the perceptual and speaker normalization warps are performed in two separate steps, perceptual warp is achieved through use of a nonlinearly distributed Mel-filterbank whereas speaker normalization is achieved through the use of an appropriate matrix transformation after the Mel cepstra have been computed.
In this paper, we integrate BLT-based speaker normalization within the perceptual MVDR (PMVDR) coefficients framework [2, 3]. First, we demonstrate that the perceptual warp is actually meant to remove some of the existing speaker differences. By estimating a specific perceptual warp factor for each speaker, it is possible to further remove these speaker-dependent differences. Then, the warp estimation process is computationally improved by integrating a binary tree search (BTS) [13] approach which reduces the computation 67% with respect to the classical VTLN. Next, performing the best warp search in the model space rather than in the feature space [14] further reduces the necessary computational resources for real-time applicability and performance. Finally, a configuration for on-the-fly implementation of this built-in speaker normalization (BISN) algorithm is proposed for an in-car speech recognition task which reduces the word error rate (WER) 24% relative to the baseline PMVDR-based system.
In Section 2, we summarize the theoretical background for the PMVDR front end which is the basis for the BISN algorithm. In Section 3, we consider the underlying meaning of so-called perceptual warping. We show via a modified LDA-based analysis [15, 16] that perceptual warping successfully removes a substantial amount of interspeaker variability. This observation leads to the idea of using a specific self-normalization warp factor for each speaker. The offline approach for the vocal-tract length normalization (VTLN) is summarized in Section 4 with its disadvantages in terms of computational efficiency. Section 5 formulates the built-in speaker normalization (BISN) algorithm in detail. Improvements to the search are introduced in Sections 5.1 and 5.2. We summarize our evaluation results in Section 6 for two different tasks, CU-Move extended digit recognition task and the speech in noisy environment (SPINE-2) task. Section 7 explains how one can easily integrate the BISN algorithm within the PMVDR framework for a real-world application. After summarizing computational considerations for the different algorithms proposed in this paper in Section 8, we make concluding remarks in Section 9.
2. The PMVDR Acoustic Front End
PMVDR is a new acoustic front end which does not use a nonlinearly spaced filterbank to incorporate perceptual considerations. Instead of using a filterbank, the FFT spectrum is directly warped before the envelope extraction stage [2, 3]. The envelope is extracted via a low-order all-pole MVDR spectrum which is shown to be superior to the linear prediction- (LP-) based envelopes [17]. Utilizing direct warping on the FFT power spectrum by removing filterbank processing avoids the smoothing effect of a filterbank and leads to preservation of almost all information that exits in the short-term speech spectrum. Also, using the MVDR method to extract the envelope contributes greatly to superior performance in noisy conditions [2, 3]. We now shortly summarize the MVDR spectrum estimation to extract the spectral envelope and the warping via interpolation algorithm to directly warp the FFT spectrum. For the details of the PMVDR computation we refer readers to [2, 3].
2.1. Minimum Variance Distortionless Response (MVDR) Spectrum Estimation
All-pole modeling is commonly used in speech spectrum analysis for speech processing applications. MVDR can be seen as an alternative all-pole modeling technique to the popular linear prediction (LP) [17]. The MVDR spectrum for all frequencies can be expressed in a parametric form. Let the  th-order MVDR spectrum be written as
th-order MVDR spectrum be written as

The parameters,  , hence the MVDR spectrum, can be easily obtained by a modest noniterative computation proposed by Musicus [18]. The parameters,
, hence the MVDR spectrum, can be easily obtained by a modest noniterative computation proposed by Musicus [18]. The parameters,  , are computed from the LP coefficients and the prediction error variance
, are computed from the LP coefficients and the prediction error variance  as
as

Therefore, the  coefficients,
coefficients,  , are sufficient to completely specify the MVDR spectrum
, are sufficient to completely specify the MVDR spectrum  .
.
2.2. Direct Warping of FFT Spectrum
It has been shown that implementing the perceptual scales through the use of a first-order all-pass system is feasible [19, 20]. In fact, both Mel and Bark scales are determined by changing the single parameter,  , of the system [20]. The transfer function,
, of the system [20]. The transfer function,  , and the phase response,
, and the phase response,  , of the system are given as
, of the system are given as


where  represents the linear frequency, while
represents the linear frequency, while  represents the warped frequency. Here, the value of
represents the warped frequency. Here, the value of  controls the degree of warping. We are more interested in the nonlinear phase response through which we implement the perceptual warping. For 16 kHz sampled signals, we set
controls the degree of warping. We are more interested in the nonlinear phase response through which we implement the perceptual warping. For 16 kHz sampled signals, we set  and
and  to approximate the Mel and Bark scales, respectively. For 8 kHz, these values are adjusted to
to approximate the Mel and Bark scales, respectively. For 8 kHz, these values are adjusted to  and
and  [20]. Bark scale performs more warping in the lower frequencies when compared to the Mel scale.
[20]. Bark scale performs more warping in the lower frequencies when compared to the Mel scale.
2.3. Implementation of Direct Warping
Warping via interpolation is a simple and fast method to implement direct warping. We would like to obtain the value of the power spectrum in the warped frequency space  by using its corresponding value in the linear-frequency space,
by using its corresponding value in the linear-frequency space,  . The inverse relation that takes us from the warped to linear frequency space can be easily obtained from (4) by replacing
. The inverse relation that takes us from the warped to linear frequency space can be easily obtained from (4) by replacing with
with :
:

A step-by-step algorithm that describes how warping can be efficiently implemented via interpolation can be given as follows.
-
(1)
Take the FFT of the input speech frame of length
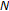 to obtain the FFT power spectrum.
to obtain the FFT power spectrum. 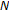 should be selected as the nearest possible power-of-2, thus providing
should be selected as the nearest possible power-of-2, thus providing 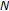 spectral points (i.e.,
spectral points (i.e., 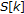 ,
,  ) in linear power spectrum space.
) in linear power spectrum space. -
(2)
Calculate
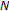 linearly spaced spectral points over the warped frequency space by dividing the entire
linearly spaced spectral points over the warped frequency space by dividing the entire 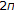 warped frequency range into
warped frequency range into  equispaced points:
equispaced points: 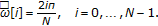 (6)
(6)
-
(3)
Compute the linear frequencies and FFT indexes that correspond to these warped frequencies using
 (7)
(7)
-
(4)
For the final step, perform an interpolation of the nearest linear spectral values to obtain the warped spectral value:
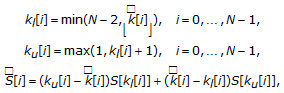 (8)
(8)
where  is the lower nearest linear FFT bin,
is the lower nearest linear FFT bin,  is the nearest upper linear FFT bin, and
is the nearest upper linear FFT bin, and  is the value of the warped power spectrum that corresponds to FFT bin
is the value of the warped power spectrum that corresponds to FFT bin  . Thus, the spectral value
. Thus, the spectral value  , at the warped frequency index
, at the warped frequency index  , is computed as the linear interpolation of nearest upper,
, is computed as the linear interpolation of nearest upper,  , and lower,
, and lower,  , spectral values in the linear frequency space.
, spectral values in the linear frequency space.
2.4. Implementation of PMVDR
In utilizing a filterbank for incorporating perceptual scales, the filterbank has two tasks, (i) warping the spectrum nonlinearly and (ii) smoothing out excitation details. In using direct warping, on the other hand, no averaging of the FFT power spectrum is used to achieve smoothing, only warping of the spectrum is performed. The smoothing is achieved through a low-order MVDR analysis that follows the warping step. Therefore, in the direct warping of the spectrum, little information is lost.
The remainder of the PMVDR algorithm can be summarized in the following steps.
-
(1)
Obtain the perceptually warped FFT power spectrum via interpolation.
-
(2)
Compute the "perceptual autocorrelation lags" by taking the IFFT of the "perceptually warped" power spectrum.
-
(3)
Perform an
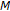 th-order LP analysis via Levinson-Durbin recursion using the perceptual autocorrelation lags [21, 22].
th-order LP analysis via Levinson-Durbin recursion using the perceptual autocorrelation lags [21, 22]. -
(4)
Calculate the
 th-order MVDR spectrum using (2) from the LP coefficients [17].
th-order MVDR spectrum using (2) from the LP coefficients [17]. -
(5)
Obtain the final cepstrum coefficients using the straightforward FFT-based approach [23]. In this implementation, after obtaining the MVDR coefficients from the perceptually warped spectrum, we take the FFT of the parametrically expressible MVDR spectrum. After applying the log operation, we apply IFFT to return back to the cepstral domain.
-
(6)
Take the first
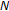 , generally 12 excluding the
, generally 12 excluding the  th-order cepstrum, cepstral coefficients as the output of the PMVDR front end. This is the cepstral truncation step.
th-order cepstrum, cepstral coefficients as the output of the PMVDR front end. This is the cepstral truncation step.
A flow diagram for the PMVDR algorithm is given in Figure 1 [3]. For further details on the PMVDR front end and its evaluation on different databases, we refer reader to [2, 3, 24].
3. The "Meaning" of Perceptual Warping
Virtually all acoustic front ends proposed for ASR use some form of nonlinear warping of the spectrum at some level. The MFCC front end, for example, uses a Mel-scaled filterbank in order to incorporate perceptual considerations. The argument for applying a nonlinear warping, or so-called perceptual warping, to the speech spectrum is strongly tied to the fact that the human auditory system performs similar processing. This is generally justified because experimental results have shown that lower frequencies of the speech spectrum carry more crucial information for ASR than higher frequencies; therefore, these frequencies are generally emphasized by a nonlinear warping function. In this section, we consider the real "meaning" of the perceptual warping from the standpoint of the interspeaker variability analysis as proposed in [15]. In all of our experiments, when a perceptual warp is introduced, it always yields better recognition accuracy (on the order of 20%, relative). We believe that there is another important "task" of the perceptual warping other than emphasizing lower frequencies. In fact, the perceptual warp was actually meant to remove some of the existing interspeaker variability in the feature set. To justify this claim, we conducted an analysis within the framework explained in [2, 15, 25]. We extracted the PMVDR features for the CU-Move in-vehicle speech [26] training set (see Section 6) (1) with no perceptual warping, (2) using the Bark scale ( ), and (3) using the BISN warp factors (see Section 5). Afterwards, we computed the variation of the trace measure (TM). The larger the TM is, the more effectively the speaker variability is removed [2, 15, 25]. Figure 2 shows the variation of the trace measure (with respect to the minimum of number speech classes and feature dimension [15]) for the three cases. The figure verifies that using the perceptual warp indeed leads to the removal of a significant amount of interspeaker variability. However, using the BISN warps specifically estimated for each speaker further removes the interspeaker variability signifying the applicability of the BISN in the context of speaker normalization.
), and (3) using the BISN warp factors (see Section 5). Afterwards, we computed the variation of the trace measure (TM). The larger the TM is, the more effectively the speaker variability is removed [2, 15, 25]. Figure 2 shows the variation of the trace measure (with respect to the minimum of number speech classes and feature dimension [15]) for the three cases. The figure verifies that using the perceptual warp indeed leads to the removal of a significant amount of interspeaker variability. However, using the BISN warps specifically estimated for each speaker further removes the interspeaker variability signifying the applicability of the BISN in the context of speaker normalization.
4. Offline VTLN
The most popular method for speaker normalization is vocal-tract length normalization (VTLN) in which the speech spectrum is linearly warped with an optimal warp factor ( ) [6, 7, 27]. The warping can also be performed by rearranging the position of the Mel filters [6, 7]. However, in the PMVDR front end, we no longer use a filterbank structure, and therefore warping is directly performed on the FFT power spectrum. In the offline VTLN application, a two-step warp needs to be performed. The first warp is called perceptual warp and applied during the extraction of acoustic features. VTLN warp also needs to be performed in cascade to the perceptual warp within the acoustic front end. The speaker-dependent parameter,
) [6, 7, 27]. The warping can also be performed by rearranging the position of the Mel filters [6, 7]. However, in the PMVDR front end, we no longer use a filterbank structure, and therefore warping is directly performed on the FFT power spectrum. In the offline VTLN application, a two-step warp needs to be performed. The first warp is called perceptual warp and applied during the extraction of acoustic features. VTLN warp also needs to be performed in cascade to the perceptual warp within the acoustic front end. The speaker-dependent parameter,  , is generally determined by conducting likelihood computations for different values within the range [0.84–1.16] (for our purpose we extend the range slightly to facilitate the binary search algorithm described in Section 5.1). Generally a single-Gaussian HMM set which is trained on all available training data is used to estimate the warp factor.
, is generally determined by conducting likelihood computations for different values within the range [0.84–1.16] (for our purpose we extend the range slightly to facilitate the binary search algorithm described in Section 5.1). Generally a single-Gaussian HMM set which is trained on all available training data is used to estimate the warp factor.
4.1. Warping Factor Estimation
Assume that we have  utterances from speaker
utterances from speaker  and would like to estimate the warp factor for this speaker. Here, we define the following terms as in [7]:
and would like to estimate the warp factor for this speaker. Here, we define the following terms as in [7]:
(i) denotes the set of feature vectors for all of the available utterances from speaker
denotes the set of feature vectors for all of the available utterances from speaker  , warped by warp factor
, warped by warp factor  ,
,
(ii) denotes the set of transcriptions of all
denotes the set of transcriptions of all  utterances,
utterances,
(iii) denotes the best warp factor for speaker
denotes the best warp factor for speaker  ,
,
(iv) denotes a given HMM trained from a large population of speakers.
denotes a given HMM trained from a large population of speakers.
The best warp factor  for speaker
for speaker  is estimated by maximizing the likelihood of the warped features with respect to the HMM model
is estimated by maximizing the likelihood of the warped features with respect to the HMM model  and transcriptions
and transcriptions  :
:

Obtaining a closed-form solution for  is difficult since the frequency warping corresponds to a highly nonlinear transformation of the speech features. Therefore, the best warp is estimated by searching over a grid of 33 points spaced evenly in the range of [0.84–1.16]. The goal of training is to obtain a canonical (normalized) set of HMMs,
is difficult since the frequency warping corresponds to a highly nonlinear transformation of the speech features. Therefore, the best warp is estimated by searching over a grid of 33 points spaced evenly in the range of [0.84–1.16]. The goal of training is to obtain a canonical (normalized) set of HMMs,  , in the sense that each speaker's utterance is warped with an appropriate warping factor and the resulting HMM is defined over a frequency-normalized feature set. Initially, the HMM set is trained from unwarped utterances, and this model is used to estimate the best warp factor for each speaker. Afterwards, every speaker's utterances are parameterized with the estimated best warp factor and then the HMM model set is re-estimated from this warped feature set. In theory, this new canonical model can be used to re-estimate the optimal warp factors, and another HMM can be trained and the procedure iterated several times. However, during our experimentation with offline VTLN, we observed that further iterating did not yield significant improvements over the first iteration, therefore we only estimate the optimal warps once and train the canonical HMMs from the feature set parameterized with these optimal warps.
, in the sense that each speaker's utterance is warped with an appropriate warping factor and the resulting HMM is defined over a frequency-normalized feature set. Initially, the HMM set is trained from unwarped utterances, and this model is used to estimate the best warp factor for each speaker. Afterwards, every speaker's utterances are parameterized with the estimated best warp factor and then the HMM model set is re-estimated from this warped feature set. In theory, this new canonical model can be used to re-estimate the optimal warp factors, and another HMM can be trained and the procedure iterated several times. However, during our experimentation with offline VTLN, we observed that further iterating did not yield significant improvements over the first iteration, therefore we only estimate the optimal warps once and train the canonical HMMs from the feature set parameterized with these optimal warps.
During recognition, our goal is to warp the frequency scale of each test utterance to best match the canonical HMMs,  . Unlike training, in the test phase, only one utterance is used to estimate
. Unlike training, in the test phase, only one utterance is used to estimate  and the transcription is not available. A general approach is to use a two-pass strategy. At first, the
and the transcription is not available. A general approach is to use a two-pass strategy. At first, the  th unwarped utterance of the
th unwarped utterance of the  th speaker,
th speaker,  and the normalized model
and the normalized model  is used to obtain a preliminary transcription of the utterance,
is used to obtain a preliminary transcription of the utterance,  . Afterwards, the optimal warp factor,
. Afterwards, the optimal warp factor,  , is estimated via the general search procedure:
, is estimated via the general search procedure:

Finally, we warp the utterance with the estimated warp factor,  and redecode using the normalized HMM model,
and redecode using the normalized HMM model,  . The output of the recognizer is our final recognition result. For offline VTLN experiments reported in this paper, however, we used all the available data from each test speaker to estimate the best warps in an offline setting (i.e., warp factors are not estimated for every single utterance).
. The output of the recognizer is our final recognition result. For offline VTLN experiments reported in this paper, however, we used all the available data from each test speaker to estimate the best warps in an offline setting (i.e., warp factors are not estimated for every single utterance).
Typically, we parameterize speech within the range of [0.84–1.16] and with a step size of 0.01 yielding a 33-point search space. Using the monotonic property, we compare the likelihoods at the current warp and at the previous warp. When the difference is negative, the best warp is found. On the average, the estimation of the best VTLN warp for a speaker requires 18 times the computational resources for one feature extraction and one likelihood computation. During the test, we must perform recognition twice in order to obtain an initial transcription to estimate the optimal warp.
5. Built-In Speaker Normalization (BISN)
Our earlier interspeaker variability analysis yielded the fact that so-called perceptual warping is in fact a speaker-normalization warping too. Motivated by this outcome, we can adjust the perceptual warp parameter specifically for each speaker and call this new warp the self-normalization warp. This should, in turn, normalize the vocal-tract length differences. Since this procedure does not require 2 applications of warping to the spectrum (one for the perceptual warp and one for the VTLN warp), as in offline VTLN, it is more efficient. Moreover, the normalization is achieved by only adjusting an internal parameter of the acoustic front end (i.e., the perceptual warp factor  ), making it a built-in procedure, hence the name built-in speaker normalization (BISN). The self-normalization warp (
), making it a built-in procedure, hence the name built-in speaker normalization (BISN). The self-normalization warp ( ) in the BISN context refers to a nonlinear mapping (as defined by (3) and (4)) whereas in the VTLN context the speaker normalization warp (
) in the BISN context refers to a nonlinear mapping (as defined by (3) and (4)) whereas in the VTLN context the speaker normalization warp ( ) refers to a linear mapping of the frequency axis.
) refers to a linear mapping of the frequency axis.
The estimation of the self-normalization warp,  , for speaker
, for speaker  , is done in a manner similar to offline VTLN. Here,
, is done in a manner similar to offline VTLN. Here,  is estimated as the one which maximizes the total likelihood of the data given a single-Gaussian HMM set. Another advantage of BISN is the reduced search space. While in classical VTLN, the search space is generally a 33-point grid, for the BISN case, using a 17-point search space yields sufficient accuracy. (In our implementation, the search was over this range, but one may reduce the dimension of the search space at the expense of performance.) In a typical setting with a perceptual warp factor of
is estimated as the one which maximizes the total likelihood of the data given a single-Gaussian HMM set. Another advantage of BISN is the reduced search space. While in classical VTLN, the search space is generally a 33-point grid, for the BISN case, using a 17-point search space yields sufficient accuracy. (In our implementation, the search was over this range, but one may reduce the dimension of the search space at the expense of performance.) In a typical setting with a perceptual warp factor of  (Bark scale at 16 kHz), the search space for the self-normalization warps can be chosen as [0.49, 0.65] reducing the search space by half versus that for VTLN. The search for the self-normalization warp within the BISN framework requires 10 times the computational resources for one feature extraction and one likelihood computation, which is still computationally expensive. The search is a computationally intensive procedure. This disadvantage has been noticed by other researchers [13]. Taking advantage of the monotonic property of the likelihood function, one can use a binary tree search [13] rather than linear search which reduces the computational load substantially with no performance loss (i.e., by producing exactly the same warp factors).
(Bark scale at 16 kHz), the search space for the self-normalization warps can be chosen as [0.49, 0.65] reducing the search space by half versus that for VTLN. The search for the self-normalization warp within the BISN framework requires 10 times the computational resources for one feature extraction and one likelihood computation, which is still computationally expensive. The search is a computationally intensive procedure. This disadvantage has been noticed by other researchers [13]. Taking advantage of the monotonic property of the likelihood function, one can use a binary tree search [13] rather than linear search which reduces the computational load substantially with no performance loss (i.e., by producing exactly the same warp factors).
5.1. Binary Tree Search (BTS) Approach
The likelihood of the data from a specific speaker is monotonically increasing (with the changing warp factor) up to a maximum, that is, until reaching the best warp, and then becomes monotonically decreasing. We present two sample likelihood variations in Figure 3 for a male and female speaker from the WSJ database [28]. For illustration purposes, the single-Gaussian HMM models for optimal warp search were trained with  and the search space was chosen to be
and the search space was chosen to be  and
and  with a step size
with a step size  resulting in a 33-point search space. In general, a step size of
resulting in a 33-point search space. In general, a step size of  provides sufficient resolution for optimal performance.
provides sufficient resolution for optimal performance.
Using this monotonic property of the likelihood function, it is possible to devise a much more efficient search algorithm than the linear search approach [13]. In [13], a Brent search was used in order to efficiently obtain the best warp factor. Without loss of generality, we will call the efficient search process as binary tree search (BTS) in this paper.
Let the single-Gaussian HMM set be trained with  (e.g.,
(e.g.,  ) and let the search space be chosen as [
) and let the search space be chosen as [ ,
,  ] (e.g., [
] (e.g., [ ,
,  ]) with a step size
]) with a step size  (e.g.,
(e.g.,  ) resulting in a
) resulting in a  -point (e.g.,
-point (e.g.,  ) one-dimensional search space, where
) one-dimensional search space, where

We can summarize the steps of the binary tree search (BTS) algorithm as follows.
-
(1)
Compute the likelihood,
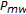 , for
, for  , where we refer to this warp as the middle warp since it is the center of our search space.
, where we refer to this warp as the middle warp since it is the center of our search space. -
(2)
Compute the lower warp as the mean of lower limit and middle warp and similarly higher warp as the mean of upper limit and middle warp as follows:
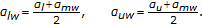 (12)
(12)
These two steps divide the warp space in half, lower region and upper region, whose middle warps are  and
and  , respectively.
, respectively.
-
(3)
Compute
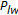 for
for 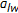 , if
, if 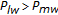 , then disregard the upper region, and consider the lower region as the new search space whose middle warp is
, then disregard the upper region, and consider the lower region as the new search space whose middle warp is 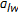 and return to Step (2). If
and return to Step (2). If 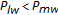 , then compute
, then compute  , for
, for 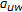 . If
. If 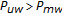 then disregard the lower region, and consider the upper region as the new search space whose middle warp is
then disregard the lower region, and consider the upper region as the new search space whose middle warp is  and return to Step (2). For the last case where
and return to Step (2). For the last case where 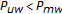 , take the new search space to be
, take the new search space to be 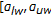 ], whose middle warp is
], whose middle warp is 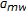 and return to Step (2). In all the cases, the search space is reduced by half.
and return to Step (2). In all the cases, the search space is reduced by half.
By recursively repeating Steps (2) and (3), we compute the optimal warp for a speaker with an average of 6 times the computational resources for one feature extraction and one likelihood computation (with the example settings above). Thus, the BTS algorithm summarized above reduces the number of likelihood computations from 10 to 6 for the BISN algorithm, exactly producing the same self-normalization warps. For BTS approach integrated within the BISN algorithm (considering a 17-point search space), the number of feature extraction and likelihood computations is 6, hence when compared with classical VTLN, it estimates the self-normalization warps with a 67% relative reduction in the computational load.
5.2. Model Versus Feature Space Search
In the current implementation, the search is conducted in the feature space. This means that the single-Gaussian HMM set is trained on unwarped features and tested on warped features for different warps throughout the search space. However, there are two motivating reasons to use the model space as the search space [14]. The first is the unaccounted Jacobian. The warped features are generated by transforming the frequency axis by a suitable warping function (speaker-dependent BLT in our case), the models, on the other hand, are trained on unwarped features. The likelihood computation, therefore, needs to be corrected using the Jacobian of the frequency transformation [14, 29]. Assume that we warp the spectra of the  th speaker by different warping factors (i.e.,
th speaker by different warping factors (i.e.,  ) and compute the warped features over time as
) and compute the warped features over time as  . Let
. Let  denote the transcription of the utterance
denote the transcription of the utterance  from speaker
from speaker  . If
. If  denotes a set of single-Gaussian HMM models trained from a large population of speakers, then the optimal warping factor for the
denotes a set of single-Gaussian HMM models trained from a large population of speakers, then the optimal warping factor for the  th speaker,
th speaker,  is obtained by maximizing the likelihood of the warped utterances with respect to the model and the transcription [14]:
is obtained by maximizing the likelihood of the warped utterances with respect to the model and the transcription [14]:

If  and
and  are the original and transformed feature vectors, respectively, for speaker
are the original and transformed feature vectors, respectively, for speaker  , then the log-likelihood of
, then the log-likelihood of  is given by
is given by

where  is the Jacobian of the transformation taking
is the Jacobian of the transformation taking  to
to  [14]. In conventional speaker normalization, the contribution of the Jacobian is not taken into account since this may cause some systematic errors in optimal warp factor estimation. When the search is conducted in the model space, the need to compensate for the Jacobian of the transformation is eliminated [14].
[14]. In conventional speaker normalization, the contribution of the Jacobian is not taken into account since this may cause some systematic errors in optimal warp factor estimation. When the search is conducted in the model space, the need to compensate for the Jacobian of the transformation is eliminated [14].
Second motivating reason is the computational gain implied by the model-based search. In the model-based search, we train a single-Gaussian HMM set for each warp in the search space offline. We then extract the features for the no warp case only once and then compute the probability for different warped models. This will reduce the heavy computational load for extracting the features over and over for each warp in the search space. Since this is integrated within the BTS approach, the model-based search only requires 1 feature extraction and 6 likelihood computations. We call this the model space-binary tree search approach (MS-BTS) which can be summarized as follows.
-
(1)
Train single-Gaussian HMM models for each warping factor in the search space. An example search space would be in the range of [0.49–0.65] with a step size of
 .
. -
(2)
For the estimation of the optimal warp, extract the features with self-normalization warp,
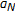 (this generally can be chosen as
(this generally can be chosen as 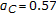 , which is the center of our search space) and then select the model (trained with
, which is the center of our search space) and then select the model (trained with 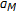 ) yielding the maximum likelihood given the warped features. The search is again performed with the BTS approach to quickly find the warped model giving the largest likelihood,
) yielding the maximum likelihood given the warped features. The search is again performed with the BTS approach to quickly find the warped model giving the largest likelihood, 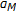 .
. -
(3)
The optimal self-normalization warp
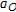 is the inverse of
is the inverse of 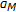 with respect to
with respect to 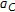 and can easily be calculated using
and can easily be calculated using  (15)
(15)
-
(4)
When the input features are extracted using the center of our search space (i.e.,
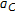 ), the above equation becomes
), the above equation becomes  (16)
(16)
After determining the self normalization warps by using the model space search approach summarized above, the rest of the normalization is similar to the offline VTLN. The canonical HMMs are trained from warped features which are extracted using appropriate self-normalization warps. During the test, same model-based approach is used to determine the self-normalization warp factors, and a two-pass recognition is performed.
Changing the search space from the feature to model space helps reducing the computational load further for estimating the optimal self-normalization warps. Now for the MS-BTS-based BISN, we need to extract the features only once and then perform 6 likelihood computations on the average to obtain the optimal self-normalization warp.
6. Experimental Framework
In order to test the effectiveness of the proposed BISN algorithm, recognition experiments were performed on two different databases that address different adverse conditions. We believe that it is important to test the speaker normalization algorithms for actual adverse environments, in order to determine if they have practical value. The databases used in the simulations are (a) CU-Move database-extended digits Portion [30], for real noisy in-car environments, (b) speech in noisy environments (SPINEs) [31], for simulated noisy military task conditions. These databases reflect good examples of environments where reliable and efficient speaker normalization is needed.
6.1. General System Description
For all experiments, we used SONIC [32, 33], the University of Colorado's HMM-based large vocabulary speech recognition system. We used a window length of 25 milliseconds and a skip rate of 10 milliseconds by Hamming windowing the frame data before further processing. The 39-dimensional feature set contains 12 statics, deltas and delta-deltas along with normalized-log energy, delta and delta-delta energy. Cepstral mean normalization (CMN) was utilized on the final feature vectors.
For both VTLN and BISN experiments, a single best warp is estimated for each speaker offline using all available data. We re-extracted PMVDR features using these best warps and retrained the HMM model set in order to obtain canonical models. During the test, a two-pass strategy was used. First, all utterances from a single speaker are recognized with noncanonical HMM set, and best warp factors are estimated using the result of this recognition. In the second step, the utterances for that speaker are extracted incorporating the best warps obtained in the first step, and a second recognition is performed with the canonical models to get the final hypothesis.
6.2. Experiments for CU-Move Extended Digits Task
For noisy speech experiments, we use the CU-Move extended digits corpus [30] which was collected in real car environments. The database and noise conditions are analyzed in [34, 35] in detail.
A total of 60 speakers balanced across gender and age (18–70 years old) were used in the training set. (Note that [34] summarizes recommended training development and test sets for the CU-Move corpus.) The test set contained another 50 speakers, again gender and age balanced. The HMMs were trained using SONIC's decision-tree HMM trainer [32, 33] resulting in a model set with approximately 10 K total Gaussians. The 40-word vocabulary is very convenient for telephone dialing applications since it contains many necessary words like "dash", "pound", "sign" in addition to numbers. We used the optimized settings ( and
and  ) for PMVDR on the CU-Move task [3].
) for PMVDR on the CU-Move task [3].
The recognition performance for different normalization approaches is given in Table 1. As we can see, the relative improvement of PMVDR integrated with BISN is close to 50% WER reduction with respect to the MFCC baseline.
Although there is no substantial improvement in the WER performance of the BISN-based techniques with respect to VTLN baseline, there is a computational gain and the convenience of performing the recognition within the acoustic front end merely changing an internal parameter. BISN-based normalization can be easily integrated into embedded systems, such as in-car speech-based navigation systems, without increasing the computational cost significantly.
6.3. Experiments for the SPINE Task
The SPINE task uses the ARCON communicability exercise (ACE) that was originally developed to test communication systems. The training data for the SPINE-2 task consists of 4 parts, (1) SPINE-1 training data (8.7 hours), (2) SPINE-1 evaluation data (7.3 hours), (3) SPINE-2 training data (3.4 hours), and (4) SPINE-2 development data (1.1 hours) totaling up to 20.5 hours of training data. The evaluation data consists of 64 talker-pair conversations which is 3.5 hours of total stereo data (2.8 hours of talk-time total). On the average, each of the 128 conversations contains 1.3 minutes of speech activity. For the SPINE-2 evaluation, a class N-gram language model is trained from the training data text. For further details about the task, we refer readers to [33]. The test data contains large segments of silence and a voice activity detector (VAD) is used to estimate speech segments. For the speaker normalization experiments, however, we preferred to use reference hand-cuts provided by NRL in order to objectively evaluate the performance of speaker normalization algorithms. We again trained gender-independent HMMs using the Sonic's decision-tree HMM trainer. The models had about 2500 clusters and around 50 K Gaussians. We used  (Mel scale at 16 kHz) and
(Mel scale at 16 kHz) and  as the settings for the PMVDR front end. The recognition performance for different speaker normalization approaches is given in Table 2. The relative improvement of PMVDR w/BISN is about 8.5% WER reduction with respect to the MFCC baseline. This moderate improvement can be attributed to the high WER of the task. Since the recognition results (hence the alignments) are not sufficiently accurate, this yields poor warp estimates. Again the WER performance is comparable with VTLN. We observe a better improvement for females versus males from the MFCC baseline.
as the settings for the PMVDR front end. The recognition performance for different speaker normalization approaches is given in Table 2. The relative improvement of PMVDR w/BISN is about 8.5% WER reduction with respect to the MFCC baseline. This moderate improvement can be attributed to the high WER of the task. Since the recognition results (hence the alignments) are not sufficiently accurate, this yields poor warp estimates. Again the WER performance is comparable with VTLN. We observe a better improvement for females versus males from the MFCC baseline.
7. Application of BISN in a Real-Time Scenario
We now would like to elaborate on the application of BISN w/MS-BTS within a real world scenario. In real time, we have all the training data in advance and can determine the self-normalization warps offline using all the available data from each speaker. However, during the test we do not have access to all speech from a specific speaker to determine the self-normalization warp for that speaker. Moreover, we do not have the information as to when speaker changes occur. So the algorithm should in fact be able to adapt the self-normalization warps to changing speakers. It should also be flexible (i.e., slowly changing) even for the same speaker to account for the slight variations in the vocal-tract characteristics. By making effective use of all the algorithms described so far, it is possible to establish a cooperation between the acoustic front end and the recognizer which will enable the front end to normalize itself automatically without the need to perform recognition twice. We give the block-diagram for the application of this self-normalization front end (BISN w/MS-BTS) in Figure 4.
Assume that we have the canonical models,  , trained on speaker-normalized training data and would like to perform online VTLN during the test. Also assume that recognition is performed for small sections of speech (i.e., utterances). We can summarize the operation of the self-normalizing front end as follows.
, trained on speaker-normalized training data and would like to perform online VTLN during the test. Also assume that recognition is performed for small sections of speech (i.e., utterances). We can summarize the operation of the self-normalizing front end as follows.
-
(i)
Parameterize first the
 th input utterance with the perceptual warp
th input utterance with the perceptual warp 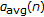 .
. -
(ii)
Recognize the utterance and pass the transcription (with alignment) information
 to the MS-BTS block.
to the MS-BTS block. -
(iii)
Determine the best self-normalization warp (i.e., the instantaneous warp
 for the current utterance
for the current utterance  ).
). -
(iv)
Pass
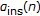 through a recursive averaging block with a forgetting factor(
through a recursive averaging block with a forgetting factor(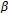 ) to obtain an averaged version (i.e.,
) to obtain an averaged version (i.e.,  ). Here, the forgetting factor
). Here, the forgetting factor 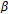 was set to 0.6, an optimization experiment is presented in this chapter later on.
was set to 0.6, an optimization experiment is presented in this chapter later on. -
(v)
Supply
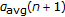 to the PMVDR front end, which is an estimate of the self-normalization warp for the
to the PMVDR front end, which is an estimate of the self-normalization warp for the  th incoming utterance.
th incoming utterance.
In summary, the front end estimates the self-normalization warp for the incoming utterance by using the self-normalization warp estimated from the earlier utterances via a recursive averaging with a forgetting factor. After performing recognition with the estimated self-normalization warp, the recognizer feeds back the alignment information so that the self-normalization warp for the next utterance can be estimated (and updated).
In this way, we never have to perform the recognition twice and sequentially we refine the warp estimate to accommodate the slight variations for the vocal-tract even for the same speaker. Moreover, the recursive averaging ensures quick adaptation of self-normalization warp to changing speakers over time. If we call the instantaneous warp estimated for the current utterance  , then the self-normalization warp estimate for the incoming utterance can be computed as follows:
, then the self-normalization warp estimate for the incoming utterance can be computed as follows:

where  is the averaged warp used in the parameterization of
is the averaged warp used in the parameterization of  th utterance,
th utterance,  is the instantaneous warp estimated for the
is the instantaneous warp estimated for the  th utterance given the features from the front end
th utterance given the features from the front end  and alignment from the recognizer
and alignment from the recognizer  , and
, and  is the estimated warp factor to be used in the parameterization of
is the estimated warp factor to be used in the parameterization of  th utterance. As an initial condition for the first utterance, we can choose to use the center warp of our search space (i.e.,
th utterance. As an initial condition for the first utterance, we can choose to use the center warp of our search space (i.e.,  ). Finally,
). Finally,  is the total number of utterances in the test set.
is the total number of utterances in the test set.  provides a means for smoothing the self-normalization warp estimate and helps accounting for the changes in vocal-tract characteristics. Since the instantaneous self-normalization warp
provides a means for smoothing the self-normalization warp estimate and helps accounting for the changes in vocal-tract characteristics. Since the instantaneous self-normalization warp  is estimated from a short segment of data (as short as one spoken digit), it fluctuates considerably. We give the variation of instantaneous self-normalization warp (
is estimated from a short segment of data (as short as one spoken digit), it fluctuates considerably. We give the variation of instantaneous self-normalization warp ( ) and recursively averaged self-normalization warp (
) and recursively averaged self-normalization warp ( ) for a comparison in Figure 5. The fixed self-normalization warps obtained from the offline BISN w/MS-BTS algorithm are also superimposed on the averaged self-normalization warp graph. The averaged self-normalization warp tracks the fixed self-normalization warp, permitting slow variations within the same speaker. Allowing some flexibility for the warp factor even within the same speaker compensates for variations which may stem from Lombard effect, stress, or a number of other physiological factors [36]. It is also shown that the averaged self-normalization warp successfully and quickly adapts to new speakers with no need to detect speaker turns.
) for a comparison in Figure 5. The fixed self-normalization warps obtained from the offline BISN w/MS-BTS algorithm are also superimposed on the averaged self-normalization warp graph. The averaged self-normalization warp tracks the fixed self-normalization warp, permitting slow variations within the same speaker. Allowing some flexibility for the warp factor even within the same speaker compensates for variations which may stem from Lombard effect, stress, or a number of other physiological factors [36]. It is also shown that the averaged self-normalization warp successfully and quickly adapts to new speakers with no need to detect speaker turns.
The variation of the instantaneous self-normalization warp ( ), averaged self-normalization warp (
), averaged self-normalization warp ( ), and fixed self-normalization warp (obtained from offline BISN w/MS-BTS), the speaker turns are also marked with a dashed line (the averaged self-normalization warp and fixed self-normalization warp are shifted upwards by
), and fixed self-normalization warp (obtained from offline BISN w/MS-BTS), the speaker turns are also marked with a dashed line (the averaged self-normalization warp and fixed self-normalization warp are shifted upwards by  for proper illustration).
for proper illustration).
As observed from Figure 5, the fluctuation in instantaneous self-normalization warp is mostly smoothed out by the recursive averaging. To determine a good value for the forgetting factor  , we conducted an experiment for a changing forgetting factor
, we conducted an experiment for a changing forgetting factor  versus WER, the results are presented in Figure 6. As observed, the particular value of
versus WER, the results are presented in Figure 6. As observed, the particular value of  is not that crucial as long as it is within the range of [0.4–0.8]. We infer that, for the CU-Move task, a good value of the forgetting factor (
is not that crucial as long as it is within the range of [0.4–0.8]. We infer that, for the CU-Move task, a good value of the forgetting factor ( ) is
) is  .
.
In Table 3, we summarize the recognition results for the CU-Move task in which each test speaker had an average of approximately 60 utterances. The results, which are slightly better than the offline experimentation, confirm the applicability of the proposed self-normalizing front end (BISN w/MS-BTS). This can be attributed to the more accurate alignments obtained during the on-the-fly normalization. In the offline case, all speech for a specific speaker is recognized first and then a warp factor is determined, since unwarped models and features are used in the first round of recognition, the recognition results (hence alignments) are moderately accurate. In the on-the-fly experimentation, however, the warp is adjusted as more and more data becomes available from the same speaker, and normalized models and features are used to update the self-normalization warp, hence the alignments supplied by the recognizer are more accurate, yielding better estimates for the self-normalization warp. We also note that for Table 3, it is not possible to directly compare BISN w/MS-BTS with VTLN, since VTLN can only be applied offline.
8. Computational Considerations
This final section aims to evaluate all algorithms in terms of their computational efficiency. We consider the number of warpings performed on the FFT spectrum (NW), the number of feature extractions (NFEs) required for the whole system (both for search and recognition), the number of likelihood computations (NLCs), and lastly the number of recognition passes (NRPs). Table 4 clearly illustrates the computational gain obtained by moving from classical VTLN to the on-the-fly version of BISN w/MS-BTS. Moving from classical VTLN to BISN eliminates the need to perform warping on the FFT spectrum twice. The perceptual and speaker normalization warps are integrated into a single speaker-dependent warp. Integration of the MS-BTS algorithm within the BISN framework for an on-the-fly application eliminates even the need to extract the features twice. Extracted features for recognition are also passed to the MS-BTS block for the self-normalization warp estimation for the incoming utterance. Since the estimation is sequential, the need to perform recognition twice is also eliminated. The self-normalization warp for the incoming utterance is recursively estimated from earlier utterances. The computational load is now reduced to realistic levels even for embedded systems. The only drawback is that we need to store all single-Gaussian models trained at each point of the search space (here we have 17 single-Gaussian models in the BISN case) in memory all the time. However, since these are only single-Gaussian models, they do not require a large amount of memory.
9. Conclusions
In this paper, we have proposed a new and efficient algorithm for performing online and efficient VTLN which can easily be implemented within the PMVDR front end. In VTLN, we need to perform warping on the spectrum twice, to accommodate perceptual considerations and to normalize for speaker differences. The proposed BISN algorithm, on the other hand, estimates a self-normalization warp for each speaker which performs both the perceptual warp and speaker normalization in a single warp. The use of a single warp to achieve both perceptual warp and VTLN warp unifies these two concepts. The model space-binary tree search (MS-BTS) algorithm was integrated to reduce the computational load in the search stage for the estimation of self-normalization warps. Moving the search base from the feature space to the model space [13] reduced the need to extract the features for each point in the search space, which in turn eliminated the need for high computational resources. A sequential on-the-fly implementation of the BISN w/MS-BTS algorithm also eliminated the need to perform multipass recognition which makes it possible to integrate this scheme with low-resource speech recognition systems.
We have shown that the BISN approach is effective for two different databases, the CU-Move in-vehicle dialog (extended digits portion) database and the SPINE military noisy speech database. The on-the-fly implementation of the BISN w/MS-BTS algorithm was also shown to be slightly more accurate than the offline version with a considerable savings in computational resources. Integrated with the BISN approach, the PMVDR front end can now be considered an intelligent front end which cooperates with the recognizer in order to automatically normalize itself with respect to the incoming speaker/speech. Since it can quickly adapt to the changing vocal-tract characteristics, it does not require any detection of speaker changes whatsoever. We believe that the PMVDR front end integrated with the strong BISN algorithm is an ideal front end for use in every system requiring noise robustness and a measurable level of speaker normalization (especially for embedded systems). It can perform acoustic feature extraction with moderate computational requirements and achieve self-normalization with respect to changing speakers very efficiently, yielding a sound acoustic front end that can be used in today's demanding speech recognition applications.
References
Hunt MJ: Spectral signal processing for ASR. Proceedings of the IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU '99), December 1999, Keystone, Colo, USA 1: 17-26.
Yapanel UH, Hansen JHL: A new perspective on feature extraction for robust in-vehicle speech recognition. Proceedings of the 8th European Conference on Speech Communication and Technology (EUROSPEECH '03), September 2003, Geneva, Switzerland 1281-1284.
Yapanel UH, Hansen JHL: A new perceptually motivated MVDR-based acoustic front-end (PMVDR) for robust automatic speech recognition. Speech Communication 2008,50(2):142-152. 10.1016/j.specom.2007.07.006
Hansen JHL: Analysis and compensation of speech under stress and noise for environmental robustness in speech recognition. Speech Communication 1996,20(1-2):151-173. 10.1016/S0167-6393(96)00050-7
Hansen JHL: Morphological constrained feature enhancement with adaptive cepstral compensation (MCE-ACC) for speech recognition in noise and Lombard effect. IEEE Transactions on Speech and Audio Processing 1994,2(4):598-614. 10.1109/89.326618
Lee L, Rose RC: Speaker normalization using efficient frequency warping procedures. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '96), May 1996, Atlanta, Ga, USA 1: 353-356.
Lee L, Rose RC: A frequency warping approach to speaker normalization. IEEE Transactions on Speech and Audio Processing 1998,6(1):49-60. 10.1109/89.650310
Andreou A, Kamm T, Cohen J: Experiments in vocal tract normalization. Proceedings of the CAIP Workshop: Frontiers in Speech Recognition II, July-August 1994, Piscataway, NJ, USA
Eide E, Gish H: A parametric approach to vocal tract length normalization. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '96), May 1996, Atlanta, Ga, USA 1: 346-348.
Acero A: Acoustical and environmental robustness in automatic speech recognition, Ph.D. thesis. Carnegie Mellon University, Pittsburgh, Pa, USA; 1990.
McDonough J: Speaker compensation with all-pass transforms, Ph.D. thesis. The John Hopkins University, Baltimore, Md, USA; 2000.
McDonough J, Byrne W, Luo X: Speaker adaptation with all-pass transforms. Proceedings of the 5th International Conference on Spoken Language Processing (ICSLP '98), November-December 1998, Sydney, Australia 6: 2307-2310.
Hain T, Woodland PC, Niesler TR, Whittaker EWD: The 1998 HTK system for transcription of conversational telephone speech. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '99), March 1999, Phoenix, Ariz, USA 57-60.
Sinha R, Umesh S: A method for compensation of Jacobian in speaker normalization. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '03), April 2003, Hong Kong 1: 560-563.
Haeb-Umbach R: Investigations on inter-speaker variability in the feature space. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '99), March 1999, Phoenix, Ariz, USA 1: 397-400.
Kim Y: Signal modeling for robust speech recognition with frequency warping and convex optimization, Ph.D. thesis. Department of Electrical Engineering, Stanford Univerity, Palo Alto, Calif, USA; 2000.
Murthi MN, Rao BD: All-pole modeling of speech based on the minimum variance distortionless response spectrum. IEEE Transactions on Speech and Audio Processing 2000,8(3):221-239. 10.1109/89.841206
Musicus BR: Fast MLM power spectrum estimation from uniformly spaced correlations. IEEE Transactions on Acoustics, Speech, and Signal Processing 1985,33(5):1333-1335. 10.1109/TASSP.1985.1164696
Smith JO III, Abel JS: Bark and ERB bilinear transforms. IEEE Transactions on Speech and Audio Processing 1999,7(6):697-708. 10.1109/89.799695
Tokuda K, Masuko T, Kobayashi T, Imai S: Mel-generalized cepstral analysis-a unified approach to speech spectral estimation. Proceedings of the International Conference on Spoken Language Processing (ICSLP '94), September 1994, Yokohama, Japan 1043-1046.
Haykin S: Adaptive Filter Theory. Prentice-Hall, Englewood Cliffs, NJ, USA; 1991.
Makhoul J: Linear prediction: a tutorial review. Proceedings of the IEEE 1975,63(4):561-580.
Oppenheim AV, Schafer RW: Discrete-Time Signal Processing. Prentice-Hall, Englewood Cliffs, NJ, USA; 1989.
Yapanel UH: Acoustic modeling and speaker normalization strategies with application to robust in-vehicle speech recognition and dialect classification, Ph.D. thesis. Center for Spoken Language Research, Department of Electrical and Computer Engineering, Univerity of Colorado at Boulder, Boulder, Colo, USA; 2005.
Yapanel UH, Dharanipragada S, Hansen JHL: Perceptual MVDR-based cepstral coefficients (PMCCs) for high accuracy speech recognition. Proceedings of the 8th European Conference on Speech Communication and Technology (EUROSPEECH '03), September 2003, Geneva, Switzerland 1829-1832.
Hansen JHL, Zhang X, Akbacak M, et al.: CU-MOVE: advanced in-vehicle speech systems for route navigation. In DSP for In-Vehicle and Mobile Systems. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2004:19-45.
Zhan P, Westphal M: Speaker normalization based on frequency warping. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '97), April 1997, Atlanta, Ga, USA 2: 1039-1042.
LDC, http://wave.ldc.upenn.edu/catalog/catalogentry.jsp?catalogid=ldc93s6a
Pitz M, Molau S, Schluter R, Ney H: Vocal tract normalization equals linear transformation in cepstral space. Proceedings of the 7th European Conference on Speech Communication and Technology (EUROSPEECH '01), September 2001, Aalborg, Denmark
Hansen JHL, Sarikaya R, Yapanel UH, Pellom B: Robust speech recognition in noise: an evaluation using the SPINE corpus. Proceedings of the 7th European Conference on Speech Communication and Technology (EUROSPEECH '01), September 2001, Aalborg, Denmark 2: 905-908.
Pellom B: SONIC: the university of colorado continuous speech recognizer. Center for Spoken Language Research, University of Colorado at Boulder, Boulder, Colo, USA; 2001.
Pellom B, Hacioglu K: Recent improvements in the CU Sonic ASR system for noisy speech: the SPINE task. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '03), April 2003, Hong Kong 1: 4-7.
Hansen JHL: Getting started with the cu-move database. The Center For Spoken Language Research, Boulder, Colo, USA; 2002.http://www.cumove.colorado.edu.com
Hansen JHL, Angkititrakul P, Plucienkowski J, et al.: CU-move: analysis & corpus development for interactive in-vehicle speech systems. Proceedings of the 7th European Conference on Speech Communication and Technology (EUROSPEECH '01), September 2001, Aalborg, Denmark 209-212.
Bou-Ghazale SE, Hansen JHL: A comparative study of traditional and newly proposed features for recognition of speech under stress. IEEE Transactions on Speech and Audio Processing 2000,8(4):429-442. 10.1109/89.848224
Acknowledgment
This work was supported by US Air Force Research Laboratory, Rome NY, under Contract no.FA8750-04-1-0058.
Author information
Authors and Affiliations
Corresponding author
Summary of Abbreviations and Acronyms
Summary of Abbreviations and Acronyms
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yapanel, U.H., Hansen, J.H. Towards an Intelligent Acoustic Front End for Automatic Speech Recognition: Built-in Speaker Normalization. J AUDIO SPEECH MUSIC PROC. 2008, 148967 (2008). https://doi.org/10.1155/2008/148967
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/148967
 to obtain the FFT power spectrum.
to obtain the FFT power spectrum. 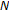 should be selected as the nearest possible power-of-2, thus providing
should be selected as the nearest possible power-of-2, thus providing 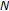 spectral points (i.e.,
spectral points (i.e., 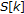 ,
,  ) in linear power spectrum space.
) in linear power spectrum space.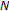 linearly spaced spectral points over the warped frequency space by dividing the entire
linearly spaced spectral points over the warped frequency space by dividing the entire 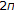 warped frequency range into
warped frequency range into  equispaced points:
equispaced points: 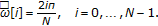

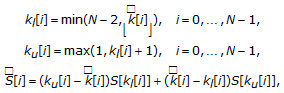
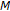 th-order LP analysis via Levinson-Durbin recursion using the perceptual autocorrelation lags [
th-order LP analysis via Levinson-Durbin recursion using the perceptual autocorrelation lags [ th-order MVDR spectrum using (2) from the LP coefficients [
th-order MVDR spectrum using (2) from the LP coefficients [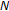 , generally 12 excluding the
, generally 12 excluding the  th-order cepstrum, cepstral coefficients as the output of the PMVDR front end. This is the cepstral truncation step.
th-order cepstrum, cepstral coefficients as the output of the PMVDR front end. This is the cepstral truncation step.


 , optimal warp for female speaker
, optimal warp for female speaker  and for male speaker
and for male speaker  is also marked.
is also marked.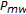 , for
, for  , where we refer to this warp as the middle warp since it is the center of our search space.
, where we refer to this warp as the middle warp since it is the center of our search space.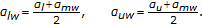
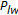 for
for 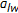 , if
, if 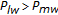 , then disregard the upper region, and consider the lower region as the new search space whose middle warp is
, then disregard the upper region, and consider the lower region as the new search space whose middle warp is 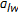 and return to Step (2). If
and return to Step (2). If 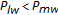 , then compute
, then compute  , for
, for 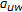 . If
. If 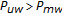 then disregard the lower region, and consider the upper region as the new search space whose middle warp is
then disregard the lower region, and consider the upper region as the new search space whose middle warp is  and return to Step (2). For the last case where
and return to Step (2). For the last case where 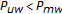 , take the new search space to be
, take the new search space to be 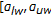 ], whose middle warp is
], whose middle warp is 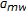 and return to Step (2). In all the cases, the search space is reduced by half.
and return to Step (2). In all the cases, the search space is reduced by half. .
.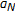 (this generally can be chosen as
(this generally can be chosen as 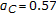 , which is the center of our search space) and then select the model (trained with
, which is the center of our search space) and then select the model (trained with 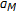 ) yielding the maximum likelihood given the warped features. The search is again performed with the BTS approach to quickly find the warped model giving the largest likelihood,
) yielding the maximum likelihood given the warped features. The search is again performed with the BTS approach to quickly find the warped model giving the largest likelihood, 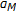 .
.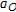 is the inverse of
is the inverse of 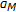 with respect to
with respect to 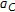 and can easily be calculated using
and can easily be calculated using 
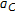 ), the above equation becomes
), the above equation becomes 

 th input utterance with the perceptual warp
th input utterance with the perceptual warp 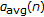 .
. to the MS-BTS block.
to the MS-BTS block. for the current utterance
for the current utterance  ).
).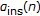 through a recursive averaging block with a forgetting factor(
through a recursive averaging block with a forgetting factor(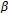 ) to obtain an averaged version (i.e.,
) to obtain an averaged version (i.e.,  ). Here, the forgetting factor
). Here, the forgetting factor 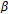 was set to 0.6, an optimization experiment is presented in this chapter later on.
was set to 0.6, an optimization experiment is presented in this chapter later on.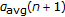 to the PMVDR front end, which is an estimate of the self-normalization warp for the
to the PMVDR front end, which is an estimate of the self-normalization warp for the  th incoming utterance.
th incoming utterance.

 ).
).