- Research Article
- Open access
- Published:
Multiple Source Localization Based on Acoustic Map De-Emphasis
EURASIP Journal on Audio, Speech, and Music Processing volume 2010, Article number: 147495 (2010)
Abstract
This paper describes a novel approach for localization of multiple sources overlapping in time. The proposed algorithm relies on acoustic maps computed in multi-microphone settings, which are descriptions of the distribution of the acoustic activity in a monitored area. Through a proper processing of the acoustic maps, the positions of two or more simultaneously active acoustic sources can be estimated in a robust way. Experimental results obtained on real data collected for this specific task show the capabilities of the given method both with distributed microphone networks and with compact arrays.
1. Introduction
During the last two decades, many efforts were devoted to investigate Speaker LOCalization (SLOC) technologies [1]. Beside early applications in audio-video conferencing, generally based on the use of small microphone arrays, more recently the interest of the scientific community on microphone networks for "ambient intelligence" has been constantly growing. In these scenarios, a microphone network consists of sets of microphones distributed in space and aimed at analyzing the acoustic scene from different perspectives; the term "multiple sources" may refer to a main source and to persons or other sources which in turn could be competitive users or interferers. In the past years, several projects addressed the SLOC task as, for instance, the CHIL EC project [2] whose main goal was to develop and integrate perceptual technologies as person tracking, event detection, distant-talking speech recognition, person identification, and so forth. Under CHIL, different person tracking systems were developed based on audio, on video, or on both modalities. In particular, it was shown that acoustic maps represent a very effective way to address the localization of one speaker given a microphone network.
One of the most critical issues under real-world conditions is the robustness of these techniques in multiple active source contexts. The automatic transcription of meetings represents a typical task where this situation occurs frequently. With this regard, multiple source localization was addressed in the past years under AMI and AMIDA EC projects for diarization tasks (http://www.amiproject.org/). Smart home is another application scenario where a multiple source context is very common. For instance, in a real domestic environment, a radio or a television may irradiate sound overlapping with a human trying to interact by voice with an automatic system. A similar application has been recently investigated in the EC funded DICIT project whose main goal was to realize a voice-enabled natural language interface able to control a TV and a Set-Top-Box at a distance of some meters from an array of microphones. Details about the project, together with public deliverables and video clips, are available at http://dicit.fbk.eu.
Typically, the solutions to both single and multiple source localization problems are based on estimations of the Time Difference Of Arrival (TDOA) at different microphone pairs, which are obtained by means of Generalized Cross-Correlation PHAse Transform (GCC-PHAT) [3], also known as Crosspower-Spectrum Phase (CSP) [4]. Solutions based on short-term spatio-temporal clustering [5, 6] and tracking algorithms as Particle Filtering (PF) [7–9] have been recently applied to the localization of multiple sources, relying on the assumption that measurements associated to all sources can be obtained with sufficient temporal density. Unfortunately, in a real environment GCC-PHAT seldom provides reliable information about all sources [10] since one of them tends to dominate over the others. If the dominant source maintains activity over a period of time, information about other sources may be lacking, making tracking difficult. An approach that partially tackles this problem is presented in [11] and relies on dispersed microphone arrays in order to get TDOA measurements related to two or more directional sources. However, as the authors state, this method does not work when a single compact array is used since there are not enough measurements associated to both sources. In a completely different perspective, as reprised in the following, a multisource algorithm for Direction Of Arrival (DOA) is presented in [12], where two maxima of a frequency-beamformer energy are obtained by putting a null in the DOA of the loudest source. Finally, other approaches have been investigated that make use of different observation measurements instead of GCC-PHAT: in [13], a likelihood function for the phase difference at two microphones for each frequency bin is implemented, in [14], mixtures of gaussians are used to model the steered beamformer output in the frequency domain and in [15] a method derived from Blind Source Separation (BSS) is presented.
In this paper we focus on two simultaneously active sources and present an approach that manipulates basic GCC-PHAT measurements in order to extrapolate and enforce the information associated to both sources. GCC-PHAT postprocessing is performed via acoustic map, which allows one to take into account implicitly some real constraints introduced by the geometry of the problem (e.g., microphone distribution in space, size of the room, etc.). As shown in the following a good choice of acoustic map is the Global Coherence Field (GCF). The approach can be extended in a straightforward manner to deal with more sources, although in many situations performance may drop as soon as the number of sources is larger than three. Typical scenarios that can benefit from the application of the proposed technique are those characterized by two or more individuals who are speaking together, with temporary overlap of their voices. Experiments on real data collected with different sensor configurations show the effectiveness of the method. In particular, the GCC-PHAT manipulation not only highlights the less dominant source but also allows one to pinpoint, and then process in the most appropriate way, potential "ghosts" which may be generated by constructive interferences in the acoustic map domain. These ghosts are often related to minor peaks in the GCC-PHAT functions, which are difficult to process in a coherent way across different microphone pairs, while they can be interpreted and compensated via acoustic maps.
A preliminary analysis on the basic idea of GCC-PHAT de-emphasis was outlined in [16], based on a limited amount of synthetic data referred to the use of a linear microphone array. The purpose of the current paper is to examine other formulations of the given technique and provide a comprehensive analysis of its effectiveness under more complex real scenarios.
Together with localization in space, in a real-world application a crucial aspect is the estimation of the number of sources that are active at each time instant. Although the purpose of this work is not to analyze in details and propose a solution for the latter estimation problem, in the remainder of this paper a statistical investigation on acoustic map maxima will be addressed, which shows the potential of these cues also when applied in deriving the number of simultaneously active sources.
The paper is organized as follows. After a description of acoustic maps for source localization in Section 2, Section 3 presents our approach to the multiple source localization problem. Experimental results are then reported in Section 4, while Section 5 investigates on automatic detection of the number of active sources. A discussion and an outlook on future development conclude the paper in Section 6.
2. Acoustic Map Analysis
As already mentioned, GCC-PHAT is still the building block of most localization algorithms presented in the literature [1] because it is capable of evaluating the coherence between two signals for each allowable time delay  . In ideal conditions GCC-PHAT presents a maximum sharp peak at a delay which is a robust estimate of the actual TDOA [4]. Among the countless localization approaches presented over the years, acoustic maps provide a very simple and effective tool to perform localization of acoustic sources when several microphone pairs are available. Let us assume that we sample the space of potential source positions and create a grid of points
. In ideal conditions GCC-PHAT presents a maximum sharp peak at a delay which is a robust estimate of the actual TDOA [4]. Among the countless localization approaches presented over the years, acoustic maps provide a very simple and effective tool to perform localization of acoustic sources when several microphone pairs are available. Let us assume that we sample the space of potential source positions and create a grid of points  . An acoustic map
. An acoustic map  is a function representing the plausibility that a source is active at a given point
is a function representing the plausibility that a source is active at a given point  and time
and time  . The dependency on time is neglected for the sake of simplicity hereafter. In ideal conditions, acoustic maps are characterized by a global maximum at the point corresponding to the actual source position. Hence the position of the source is estimated by picking the maximum peak of
. The dependency on time is neglected for the sake of simplicity hereafter. In ideal conditions, acoustic maps are characterized by a global maximum at the point corresponding to the actual source position. Hence the position of the source is estimated by picking the maximum peak of 

Since acoustic maps introduce a spatial discretization, beside the temporal sampling of signals, some artifacts or aliasing may be introduced if the density of  is not high enough. In this study, we set up the experimental framework to reduce the impact of this possible bias.
is not high enough. In this study, we set up the experimental framework to reduce the impact of this possible bias.
Given  microphone pairs and a GCC-PHAT function
microphone pairs and a GCC-PHAT function  for each pair
for each pair  ,
,  , there are several different ways to define an acoustic map. A common technique implements a Least-Squares (LS) approach by considering for each pair
, there are several different ways to define an acoustic map. A common technique implements a Least-Squares (LS) approach by considering for each pair  the time lag
the time lag  that maximizes
that maximizes 

The acoustic map based on the LS criterion is computed as follows [17]:

where  is the geometrically computed TDOA at microphone pair
is the geometrically computed TDOA at microphone pair  when the source is assumed to be in
when the source is assumed to be in  .
.
As mentioned before, one of the most effective acoustic maps is the so called Global Coherence Field that was introduced in [18]. For a given point  , the value of the map is computed according to
, the value of the map is computed according to

For a microphone pair  , a peak of the GCC-PHAT function
, a peak of the GCC-PHAT function  is projected onto the GCF map as a hyperbolic distribution of points characterized by a high magnitude, and with a dispersion that increases with the distance of the point from the two microphones. Summing the projections, computed over the entire set of microphone pairs, gives rise to GCF peaks resulting from constructive interference between the above mentioned hyperbolic distribution of points, as shown in Figure 1. Thanks to this mechanism of coherent recombination, the resulting GCF acoustic map can even reveal the possible relevance of low magnitude peaks of the GCC-PHAT functions, which may refer to early reflections.
is projected onto the GCF map as a hyperbolic distribution of points characterized by a high magnitude, and with a dispersion that increases with the distance of the point from the two microphones. Summing the projections, computed over the entire set of microphone pairs, gives rise to GCF peaks resulting from constructive interference between the above mentioned hyperbolic distribution of points, as shown in Figure 1. Thanks to this mechanism of coherent recombination, the resulting GCF acoustic map can even reveal the possible relevance of low magnitude peaks of the GCC-PHAT functions, which may refer to early reflections.
Examples of GCF functions when using different sensors of the setup depicted in Figure 7. The source is in central position and oriented downward (P4 in Figure 7). Figure (a) shows the GCC-PHAT functions computed at 4 microphone pairs (only a subset of delays is reported in the figure; the maximum possible delay would be 52 samples). Figure (b) shows the GCF map when Pair 1 and Pair 2 are used microphone positions are represented by white semicircles in the GCF maps. Figure (c) depicts the map based on Pair 5 and Pair 6: note how the hyperbolas would cross each other outside the room in the location of an image source. In figure (d), the map resulting from the combination of the 4 pairs is reported. Finally, Figure (e) shows the map obtained when using 7 microphone pairs.
GCF is also known as Steered Response Power PHAse Transform (SRP-PHAT) [1] and there are several implementations (e.g., [19, 20]) and variations (e.g., [21]) of this method. Among these variations, GCF was extended in [22] to the Oriented Global Coherence Field (OGCF) that deduces information about the orientation of a non-omnidirectional source. In particular, OGCF is useful when directive sources are dealt with and microphones are distributed in pairs surrounding the area of interest. If we consider a set of  potential angular orientations, OGCF is computed for each point
potential angular orientations, OGCF is computed for each point  and each orientation
and each orientation  as follows
as follows

where  is a weight meant to give more emphasis to those microphone pairs which are frontal to a source aiming at the given direction
is a weight meant to give more emphasis to those microphone pairs which are frontal to a source aiming at the given direction  (i.e., direct wavefronts impinge on them) [22, 23]. This weight is computed as:
(i.e., direct wavefronts impinge on them) [22, 23]. This weight is computed as:

where the parameter  must be selected taking into account the source directivity as well as the microphone spatial distribution.
must be selected taking into account the source directivity as well as the microphone spatial distribution.  is the angular distance between the orientation
is the angular distance between the orientation  and the line connecting the position
and the line connecting the position  and the microphone pair
and the microphone pair  . It can be easily shown that the Gaussian weighting function adopted in this work is a convenient choice for handling various cardioid-like emission patterns. Given the position of the source, which can be estimated through GCF maximization, OGCF provides a sort of radiation pattern of the source (Figure 2) from which the most likely orientation can be derived. A spatial map, named M-OGCF, can then be obtained from OGCF through local maximization over all orientations for each
. It can be easily shown that the Gaussian weighting function adopted in this work is a convenient choice for handling various cardioid-like emission patterns. Given the position of the source, which can be estimated through GCF maximization, OGCF provides a sort of radiation pattern of the source (Figure 2) from which the most likely orientation can be derived. A spatial map, named M-OGCF, can then be obtained from OGCF through local maximization over all orientations for each  :
:

Examples of OGCF(s, o) computed at the point that maximizes GCF with N p = 7 and N o = 128. The figure refers to a case where the source is in a central position of the room in Figure 7 and oriented approximately toward -π/2. The inner curves are obtained using only microphone pairs 1-2 and 5-6, respectively, (see Figure 1). The external curve corresponds to the use of 7 microphone pairs. Arrows indicate the directions corresponding to the maximum values of each OGCF function. The scale for OGCF values is logarithmic.
2.1. Acoustic Maps with Multiple Sources
As the literature shows, the given acoustic maps represent efficient tools to localize a single source, even in moderately reverberant environments. Although they were not conceived to process simultaneously active sources, in the latter situation they often exhibit several peaks that can be exploited to localize at least the main source. In practice, in most of these cases a source is predominant over the others which consequently manifest a lower coherence at most of the sensor pairs. This phenomenon is due to different dynamics and spectral contents as well as to different propagation patterns and is observed in the GCC-PHAT function too [10], that is, it is not due to the map computation. It must also be considered that the GCC-PHAT is a nonlinear operator and therefore the principle of superposition of effects does not strictly hold. As a consequence, even if the position of the dominant source can always be correctly determined, a simple search for the second maximum within the acoustic map hardly ever allows the localization of the secondary source position. In specific favorable conditions, the peaks alternate in time, and therefore a memory-based algorithm can keep track of the positions of two sources, for instance by means of short-term spatio-temporal clustering [6]. The examples of Figure 3 show the  -coordinate of the maximum peak of a GCF map along time when two sources are active. Notice in Figure 3(a) how the estimated coordinate keeps on jumping from one source to the other. Conversely, when one source is predominant in the long term, as shown in Figure 3(b), only few observations of the position of the weaker source are available. Very long observation intervals are then required to detect the second source, resulting in huge processing delays and latency in real-time tracking.
-coordinate of the maximum peak of a GCF map along time when two sources are active. Notice in Figure 3(a) how the estimated coordinate keeps on jumping from one source to the other. Conversely, when one source is predominant in the long term, as shown in Figure 3(b), only few observations of the position of the weaker source are available. Very long observation intervals are then required to detect the second source, resulting in huge processing delays and latency in real-time tracking.
Positions of the peak in a GCF map when two sources are active. The horizontal axis represents time while the vertical axis shows the x-coordinate related to the located sources. Actual source positions are indicated by continuous lines. In (a) the estimated coordinate, represented by dots, jumps from one source to the other, while in (b) one of the sources is almost always predominant.
Moreover, when operating with several distributed microphone pairs, the problem is further complicated by possible constructive interferences that generate ghost peaks in the map. Figure 4 shows an example of ghosts generated by GCC-PHAT peaks referred either to active sources or to early reflections. The position of Speaker 1 can be derived in a straightforward manner by maximizing the GCF acoustic map, or by taking into account the GCC-PHAT maxima referred to the first two microphone pairs. However, deriving the position of Speaker 2 becomes difficult due to misleading peaks both in the GCC-PHAT domain and in the GCF domain. It is worth noting that this example corresponds to a simplified representation of that analyzed in Figure 9 of the experimental section. It sketches a typical real-world situation, where normally GCC-PHAT functions are characterized by several minor peaks related either to active sound sources or to early reflections [24], while GCF acoustic maps provide a more effective representation to deduce source positions.
A synthetic example, derived from the case analyzed in Figure 9, which describes the contributions of GCC-PHAT functions to the GCF computation. For the sake of simplicity, hyperbolas have been replaced by lines. The dashed peak (in the GCC-PHAT) and line (in the map) correspond to the effect of a reflection on the wall. Figure (a) shows “simplified” GCC-PHAT functions consisting of few impulses. Figure (b) depicts the corresponding GCF map; lines correspond to peaks in the GCC-PHAT functions. Numbers close to intersections represent the amplitude of the map peaks resulting fromthe combination of GCC-PHAT peaks in Figure (a). Note that GCF has a maximum corresponding to Speaker 1 position, and that other peaks (ghosts), exceeding that in Speaker 2 position, are generated by constructive interference.
3. Proposed Approach
The previous section highlighted some problems that can be found, even in single speaker localization, when directly processing either GCC-PHAT functions or GCF acoustic maps. In order to extend acoustic map analysis to the multiple source case, we present a novel method that attempts to de-emphasize the dominant source, after it has been detected, in order to let the other sources stand out. For the sake of simplicity we consider only two sources overlapping in time. Our proposed method can be split into 4 steps.
-
(1)
Given an acoustic map
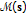 based on (3), (4) or (7), take the coordinates
based on (3), (4) or (7), take the coordinates  of the map maximum as estimate of the dominant source position (the position of the peak may be derived from the current observations only, or could result from a more articulated tracking algorithm),
of the map maximum as estimate of the dominant source position (the position of the peak may be derived from the current observations only, or could result from a more articulated tracking algorithm), -
(2)
For each microphone pair
 , derive a new GCC-PHAT function
, derive a new GCC-PHAT function 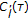 by reducing the magnitude of the original function
by reducing the magnitude of the original function  for
for  close to
close to  ,
, -
(3)
Compute a new map
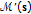 using the
using the 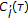 functions,
functions, -
(4)
Search for the maximum of
 and take its coordinates
and take its coordinates  as estimate of the lower-rank source position.
as estimate of the lower-rank source position.
The core of the method is the GCC-PHAT de-emphasis performed in Step (2) which will be described in Section 3.1.
One of the main advantages of this approach is that removing contributions associated to the dominant source at GCC-PHAT level enables also the removal of peaks in the GCF map that are associated to ghost sources. For instance, applying it to the example in Figure 4 all the given four ghosts would disappear and Speaker 2 could be localized. In practice, de-emphasizing GCC-PHAT for a given microphone pair at delays related to the primary peak corresponds to reduce GCF scores at the related hyperbolic distribution of points which includes the position of the located dominant source.
The algorithm can be extended to deal with more than two acoustic sources by iterating steps from (2) to (4). However, due to background noise and reverberation, the performance drops considerably when dealing with three or more sources. In the latter case, a smart combination of the proposed de-emphasis technique with memory-based tracking schemes allows localization of sources that alternate their acoustic activity in time.
It is worth noting that a similar mechanism was exploited in [12]. However, that algorithm was limited to a DOA estimation based on the maximum of GCC-PHAT function; hence, it did not address problems related to ghosts. The localization of multiple sources was achieved by applying a null to the beamformer output at the time delay associated to the loudest source. As a consequence, slight deviations in the estimation of the position of the source may result in putting the null at wrong time delays, vanishing the effect of the null itself. In other words, the method is robust in simple situations and with the use of a single array; however, it generally fails when distributed arrays are used, and when early reflections and head orientation issues are to be addressed.
3.1. GCC-PHAT De-Emphasis
Let us consider the microphone pair  and its corresponding function
and its corresponding function  . Given the time delay
. Given the time delay  associated to the dominant source, a modified version of GCC-PHAT
associated to the dominant source, a modified version of GCC-PHAT  is computed by applying a mask to
is computed by applying a mask to 

Among several possible alternatives, we adopt the following notch function  :
:

where parameters  and
and  determine the sharpness of the notch, while
determine the sharpness of the notch, while  is a normalization factor updated for each frame to guarantee that:
is a normalization factor updated for each frame to guarantee that:

where  is the maximum time delay determined by the inter-microphone distance. The goal of
is the maximum time delay determined by the inter-microphone distance. The goal of  is to redistribute over the time lags the coherence removed around
is to redistribute over the time lags the coherence removed around  .
.
As shown in Figure 5, in practice a sort of sharp notch-filter is applied in the lag domain to filter out GCC-PHAT at  . Small values of
. Small values of  generate very selective de-emphasis functions in the sense that the difference in attenuation between the null and the adjacent time delays is very high. Conversely, large values of
generate very selective de-emphasis functions in the sense that the difference in attenuation between the null and the adjacent time delays is very high. Conversely, large values of  yield a considerable attenuation also for time delays in the neighborhood of the targeted one. The parameter
yield a considerable attenuation also for time delays in the neighborhood of the targeted one. The parameter  determines the sharpness of the function by controlling the width of the notch. In this sense, we can distinguish between wide and sharp masks. When
determines the sharpness of the function by controlling the width of the notch. In this sense, we can distinguish between wide and sharp masks. When  ,
,  is flat and no de-emphasis is performed.
is flat and no de-emphasis is performed.
In Figure 6 one can appreciate the effects of de-emphasis on a GCC-PHAT function. Figure 6(a) shows the original function when two speakers are active and the corresponding TDOAs are −1.1 and 17.7 samples. Note that a peak is present at the time lag associated to each source, although the one at negative lag is considerably higher. Figure 6(b) depicts  when
when  and
and  : the main peak has been removed and the second one can be now identified. On the other hand, in Figures 6(c) and 6(d), where sharper and more selective
: the main peak has been removed and the second one can be now identified. On the other hand, in Figures 6(c) and 6(d), where sharper and more selective  are used, the removal of the main peak is less effective and it fails in the latter case. Choosing an appropriate de-emphasis function is, hence, fundamental in order to obtain satisfactory performance. From a general point of view, a wide and less selective de-emphasis is preferable because
are used, the removal of the main peak is less effective and it fails in the latter case. Choosing an appropriate de-emphasis function is, hence, fundamental in order to obtain satisfactory performance. From a general point of view, a wide and less selective de-emphasis is preferable because  comes from an inherently noisy estimation process. On the other hand, if the TDOAs of two sources are only few samples apart, a sharp function allows the removal of one source without affecting the second one. Therefore, a careful tradeoff must be found depending on the characteristics of the application and of the expected source positions (if a priori knowledge is available) and according to the sensor deployment and the environmental acoustics.
comes from an inherently noisy estimation process. On the other hand, if the TDOAs of two sources are only few samples apart, a sharp function allows the removal of one source without affecting the second one. Therefore, a careful tradeoff must be found depending on the characteristics of the application and of the expected source positions (if a priori knowledge is available) and according to the sensor deployment and the environmental acoustics.
Example of GCC-PHAT functions before and after de-emphasis. The true TDOAs are −1.1 and 17.7 samples. The vertical line represents the delay of the dominant source. Figure (a) shows the original function. Figure (b) refers to a wide de-emphasis (b = 4.5 and p = 1.5) while (c) shows how  changes when a selective notch is adopted (b = 2.5 and p = 0.5). Finally Figure (d) shows the result of applying a very selective function (b = 1.5 and p = 0.2).
changes when a selective notch is adopted (b = 2.5 and p = 0.5). Finally Figure (d) shows the result of applying a very selective function (b = 1.5 and p = 0.2).
4. Experimental Analysis
The proposed algorithm was evaluated on real data acquired with two different sensor settings: the first one implements a Distributed Microphone Network (DMN) that consists of a set of microphones distributed in space to observe an acoustic scene from different points, while the second one consists of a linear array. Data and references are available for download at the following link: http://shine.fbk.eu/people/brutti/database. Three acoustic map methods are taken into account in this analysis: LS, GCF and M-OGCF. The LS map is used in this study as reference for GCF and M-OGCF, due to its low computational requirements.
In order to simulate overlapping sources, a talker was recorded while uttering some sentences in different positions and orientations. Recorded signals from each single-source session were then summed up. The peak search was restricted to a 2-dimensional space and the resolution of the grid  was 2 cm. The sampling rate was 44.1 kHz in the DMN and 48 kHz in the linear array case. In both settings, the number of orientations
was 2 cm. The sampling rate was 44.1 kHz in the DMN and 48 kHz in the linear array case. In both settings, the number of orientations  for M-OGCF computation was 32 and
for M-OGCF computation was 32 and  in (5) was 2. The length of the signal chunks processed for FFT computation was set to 214 samples with 75% overlap between consecutive sequences of samples. The two position estimates were constrained to be at least 50 cm apart from each other.
in (5) was 2. The length of the signal chunks processed for FFT computation was set to 214 samples with 75% overlap between consecutive sequences of samples. The two position estimates were constrained to be at least 50 cm apart from each other.
In order to measure the improvement provided by the proposed approach, a baseline localization method was used for reference which simply derives the first and second highest peaks of the acoustic map. As upper bound we considered the performance when the sources are active in a nonsimultaneous way, and the localization algorithm is applied to each of the two given maps.
4.1. Metrics
The performance of the proposed localization algorithm were measured in terms of "double localization rate" ( ). Let us denote with
). Let us denote with  and
and  the estimated and the actual positions, respectively, for the
the estimated and the actual positions, respectively, for the  th source
th source  at time frame
at time frame  . The localization error is defined as the euclidean distance between the estimated and the actual positions
. The localization error is defined as the euclidean distance between the estimated and the actual positions

Considering only those frames when both sources are active (the signals were manually transcribed in order to establish speech activity intervals for each speaker) and denoting with  the number of localizations for which both
the number of localizations for which both  and
and  are lower than 20 cm, and with
are lower than 20 cm, and with  the total number of estimates,
the total number of estimates,  is defined as
is defined as

Since the given procedure does not aim at providing the identification of each source, estimates  are associated to sources based on a minimum distance criterion. The use of
are associated to sources based on a minimum distance criterion. The use of  , instead of a metric based on the euclidean distance, is necessary to reduce potential bias in the results due to inaccurate reference coordinates of human speakers.
, instead of a metric based on the euclidean distance, is necessary to reduce potential bias in the results due to inaccurate reference coordinates of human speakers.
4.2. Distributed Microphone Network
As a first study case we consider a DMN, as the one adopted in the CHIL project, which consists of 7 arrays, each one including 3 microphones placed along a horizontal line at 20-cm distance each other. The positions of the 7 arrays are shown in Figure 7 where they are labeled as T0-T6. Since we did not consider pairs consisting of microphones from different arrays, the resulting number of used pairs is  . The DMN is installed in a room whose dimensions are
. The DMN is installed in a room whose dimensions are  m. Its reverberation time RT60 is equal to
m. Its reverberation time RT60 is equal to  s. Based on measurements of Direct-to-Reverberation Ratios using different sources (e.g., a loudspeaker diffusing white gaussian noise and a real human speaker) located in different positions, a critical distance ranging between 2 meters (human speaker) and 3 meters (loudspeaker) was observed. Actually, the range is due to the fact that critical distance depends on the source directivity. With this regard, speaker orientation also represents an important issue in our experimental task. The given critical distance and RT60 estimates confirm that the experiments described in the following section are characterized by the presence of quite strong early reflections and reverberation tails in the signals acquired by most of the microphone pairs.
s. Based on measurements of Direct-to-Reverberation Ratios using different sources (e.g., a loudspeaker diffusing white gaussian noise and a real human speaker) located in different positions, a critical distance ranging between 2 meters (human speaker) and 3 meters (loudspeaker) was observed. Actually, the range is due to the fact that critical distance depends on the source directivity. With this regard, speaker orientation also represents an important issue in our experimental task. The given critical distance and RT60 estimates confirm that the experiments described in the following section are characterized by the presence of quite strong early reflections and reverberation tails in the signals acquired by most of the microphone pairs.
As discussed in Section 2, in a DMN scenario, the subset of microphone pairs that capture direct soundwaves emitted by a source is more useful for localization purposes. The microphones placed at the back of a directional source receive mainly reflections, and hence, do not provide a reliable contribution to deduce the location of sound emission. In the given DMN configuration, if two sources are frontal to separate subsets of microphone pairs, the weak source may result quite evident even without de-emphasis. However, ghost peaks can be generated as outlined in Section 2. These phenomena depend on the relative positions and orientations of the sources with respect to the sensors and a reliable model is hardly achievable due to its complexity and variability.
Five speaker positions were taken into account as shown Figure 7. Since human speakers are directional sources, the orientation is also shown by means of an arrow. A sentence of approximately 10 seconds was uttered at each position, which was at least 1.5 meters away from the closest microphone and at more than 3 meter distance from the frontal microphones.
Figure 8 shows examples of GCF maps when two sources are active in positions P1 and P5. Figure 8(a) reports the map before the de-emphasis process, while Figure 8(b) shows the resulting map after the dominant source has been removed ( ,
,  ). Finally, Figure 8(c) shows the GCF map when a more selective de-emphasis function is applied (
). Finally, Figure 8(c) shows the GCF map when a more selective de-emphasis function is applied ( and
and  ). Color and detailed figures depicting the same maps are available on-line at http://shine.fbk.eu/people/brutti/jaspmp/jaspmp.html.
). Color and detailed figures depicting the same maps are available on-line at http://shine.fbk.eu/people/brutti/jaspmp/jaspmp.html.
In the previous example, the two sources are quite evident even in the original map because different sensor pairs contribute to give rise to different peaks. Let us consider the maps in Figure 9 which refer to two sources in positions P2 and P4. Here the amplitude of the peak associated to the secondary source (i.e., P4) is lower than the amplitude of two ghost peaks which are located just on the left and on the right of P4 in the lower part of the map. As shown in Figure 9(b), de-emphasis allows a clear identification of the second source.
4.2.1. Results
First of all, performance in terms of  is analyzed over all the combinations of the five positions. Figure 10 shows the averaged
is analyzed over all the combinations of the five positions. Figure 10 shows the averaged  for different de-emphasis parameter settings and different acoustic map computation methods. Full square and circle represent the baseline and the upper bound, respectively. Table 1 reports on the best average performance delivered by each map method in contrast with the baseline and the upper bound. The table reports also the de-emphasis parameter sets that maximize
for different de-emphasis parameter settings and different acoustic map computation methods. Full square and circle represent the baseline and the upper bound, respectively. Table 1 reports on the best average performance delivered by each map method in contrast with the baseline and the upper bound. The table reports also the de-emphasis parameter sets that maximize  .
.
From the given results, it is clear that on average the proposed algorithm provides a gain with respect to an approach which does not implement de-emphasis. Notice that GCF and M-OGCF baselines are quite good thanks to the distributed nature of the sensor set up and to the full use of GCC-PHAT information, while the LS baseline is very poor because it uses only the time lags associated to GCC-PHAT maximum peaks.
GCF and M-OGCF seem to deliver very similar results, with the latter performing slightly better. Regarding GCF, the best performance is achieved using relatively small values of  (
( ) and values of
) and values of  ranging between 2 and 4. Notice how performance in Figure 10(a) degrades rapidly as soon as
ranging between 2 and 4. Notice how performance in Figure 10(a) degrades rapidly as soon as  increases and
increases and  is larger than 1. As far as M-OGCF is concerned, a similar trend is observed in Figure 10(b). Optimal values for
is larger than 1. As far as M-OGCF is concerned, a similar trend is observed in Figure 10(b). Optimal values for  are between 1.5, and 4 and
are between 1.5, and 4 and  should be chosen between 0.2 and 0.7. The fact that M-OGCF accentuates the contributions of frontal pairs, through a proper weighting, makes the system less sensitive to the choice of the de-emphasis parameters. For what concerns the LS map, although it performs worse than the other two approaches, the gain with respect to the baseline is considerable.
should be chosen between 0.2 and 0.7. The fact that M-OGCF accentuates the contributions of frontal pairs, through a proper weighting, makes the system less sensitive to the choice of the de-emphasis parameters. For what concerns the LS map, although it performs worse than the other two approaches, the gain with respect to the baseline is considerable.
Analysis of Single Cases
The previous discussion was based on average performance over all the combinations under investigation. Let us focus on single cases to analyze the convenience of the proposed approach from different perspectives. This convenience may vary considerably, depending both on the relative positions and on the distribution of the microphone pairs that are impinged by direct waves. In the following, we do not consider LS since it performs much worse than the other two maps. Let us denote as ( ,
,  ) the best local parameters, that is, those parameters maximizing locally the performance. Table 2 reports on the corresponding performance for each source combination. The final row of the table indicates the average performance when using the best parameter set for each source combination which clearly gives an improvement with respect to using the same parameters for all source positions (see results in Table 1).
) the best local parameters, that is, those parameters maximizing locally the performance. Table 2 reports on the corresponding performance for each source combination. The final row of the table indicates the average performance when using the best parameter set for each source combination which clearly gives an improvement with respect to using the same parameters for all source positions (see results in Table 1).
Although the average performance is reasonably good, processing some source combinations leads to some discrepancies in the results. As shown in Figure 10(d), the combination P1-P3 presents a particular behavior, which deserves a more detailed analysis. As evidenced by the GCF maps shown in Figure 11, in this case the T2 array is directly affected by both sources and hence the notch filter must be very selective in order to guarantee an effective estimation of the second source location. As a confirmation, Figure 10(d) shows that when  and
and  ,
,  decreases because the resulting
decreases because the resulting  is too wide. Figure 11(b) depicts the map after a very selective de-emphasis is applied: the dominant source (i.e., P3) is removed and the secondary peak (see the circle in the figure) still benefits from the T2 contribution. Conversely, Figure 11(c) shows the resulting map when a wider de-emphasis is performed: the contribution of T2 has been removed and the peak associated to P1 is no longer present.
is too wide. Figure 11(b) depicts the map after a very selective de-emphasis is applied: the dominant source (i.e., P3) is removed and the secondary peak (see the circle in the figure) still benefits from the T2 contribution. Conversely, Figure 11(c) shows the resulting map when a wider de-emphasis is performed: the contribution of T2 has been removed and the peak associated to P1 is no longer present.
GCF maps when sources are in P1 and P3. (a) shows the original map: the presence of the dominant source in P3 compresses the function dynamics at other points. (b) shows the map after a selective de-emphasis (b = 0.5 and p = 1.5) is performed: the secondary source in P1 is now evident (in the circle). Conversely, in (c) a wider  (b = 5.5 and p = 1.5) is applied which removes completely the contribution of T2 and hence eliminates also the peak associated to P1.
(b = 5.5 and p = 1.5) is applied which removes completely the contribution of T2 and hence eliminates also the peak associated to P1.
From this analysis, it is clear that average performance derives from a set of quite different experimental situations. For some of them, adapting the de-emphasis process to the mutual source positions and orientations could give a further improvement to performance.
4.3. Linear Array
In many application contexts, a DMN solution, with microphones all around the walls of a room, cannot be adopted and instead a compact array, typically a linear one, has to be employed. Although this sensor configuration offers a reduced spatial coverage and is not robust in estimating the distance from the array, the presence of more microphone pairs close to each other permits an effective multichannel processing that ensures a robust estimation of the direction of arrivals (i.e., the azimuthal angle). In general, localization algorithms with linear arrays are evaluated in terms of azimuth error. Here, we consider again the 2D localization error for an easier, although more challenging, comparison with results presented in Section 4.2.
As shown in Figure 12(b), in this work a harmonic array of 13 microphones was used. The array was specifically designed, under the DICIT project, to allow its subdivision in 4 linear subarrays with different inter-microphone distances. In the following experiments, we used a subset of 7 microphones spaced of 32 cm, which allowed us to derive acoustic maps from 6 microphone pairs. Similarly to the DMN case, 5 positions were taken into account as reported in Figure 12(a). However, the combination P3-P5 was excluded because it is not tractable in the current sensor setting with the method under analysis. By means of arrows, the figure shows also the orientation of the speakers, which are always facing the array. The room dimensions are  m and the reverberation time RT60 is about 0.15 s. In each position the source was more than 1.5 meters away from the center of the array.
m and the reverberation time RT60 is about 0.15 s. In each position the source was more than 1.5 meters away from the center of the array.
Scheme of the experimental settings in the linear array scenario. Figure (a) depicts the room map with the source positions under investigation. The bar on the right represents the linear array which was installed at a height of 1.5 meters. Note that a window is present on the wall at the bottom. Figure (b) shows the geometry of the harmonic array used in the data recordings. Circles identify the microphones that were used for source localization.
4.3.1. Results
Figure 13 reports the average performance over the different position combinations, and Table 3 summarizes the results comparing them with both the baseline and the upper bound.
First of all, notice that baseline results are much lower than in the DMN case because in this configuration different source orientations can not be processed in an effective way due to the limited spatial extent of the microphone array. As a result, in the baseline the source is often localized in the right direction (small azimuth error) but with a quite large distance error. Using the GCF map, the best performance is achieved with  and
and  which leads to
which leads to  . In contrast with what was observed in the DMN case, large values of
. In contrast with what was observed in the DMN case, large values of  offer the best performance. A wider de-emphasis mask is preferable in general if the source positions and the microphone deployment permit it. In the current setting, the maximum peak of the map is based on contributions provided by all the microphone pairs (the speakers are always facing the array); therefore removing the contribution of a pair, due to the de-emphasis process, is not so detrimental as in the DMN scenario. Similar results are obtained with M-OGCF, which however can not be fully exploited in this sensor configuration due to the nonsurrounding nature of the array, yielding slightly worse performance than GCF. Finally, also when the LS map is employed the proposed approach provides a considerable gain in performance over the related baseline, although the overall result is below those obtained with the other maps.
offer the best performance. A wider de-emphasis mask is preferable in general if the source positions and the microphone deployment permit it. In the current setting, the maximum peak of the map is based on contributions provided by all the microphone pairs (the speakers are always facing the array); therefore removing the contribution of a pair, due to the de-emphasis process, is not so detrimental as in the DMN scenario. Similar results are obtained with M-OGCF, which however can not be fully exploited in this sensor configuration due to the nonsurrounding nature of the array, yielding slightly worse performance than GCF. Finally, also when the LS map is employed the proposed approach provides a considerable gain in performance over the related baseline, although the overall result is below those obtained with the other maps.
As in the DMN case, GCF and M-OGCF results are reported for each source combination in Table 4. In general, the trend is very similar to the average case and it is clear that the proposed method always outperforms the baseline. As for P2-P5, even though the performance is still above the baseline, in this configuration the algorithm performs worse than the average. A more detailed analysis reveals that the algorithm fails to estimate the position of P2. In particular, the estimation of the DOA is accurate while most of the errors concentrate in estimating the distance from the microphones. It is likely that the given loss is related to some acoustic properties of the room (e.g., the window in Figure 12(b)).
5. Estimation of the Number of Active Sources
As mentioned in the introduction, in the given application context detecting the number of active speakers at each time instant represents another crucial task. Although the main focus of the paper is on localization, in this section we will briefly show how the acoustic map peaks can also be used as cues to estimate the number of active sources. In general, algorithms for speech activity detection are based on acoustic features (e.g., energy) and on their temporal correlation that generally provides more robustness rather than processing each frame independently [25, 26]. In our investigation, for the sake of simplicity and to emphasize better the properties of the given cues, the focus will be limited to an analysis based on a single frame or on two adjacent frames.
Let us denote with  the hypothesis that there are no active sources and with
the hypothesis that there are no active sources and with  the hypothesis that at least one source is active. We consider the statistical distributions of the map maximum peak under the two hypotheses, that is,
the hypothesis that at least one source is active. We consider the statistical distributions of the map maximum peak under the two hypotheses, that is,  and
and  , respectively. Figure 14(a) shows the two distributions obtained from the data set collected in the DMN case when using the GCF map. The two distributions are clearly distinct and the detection of the presence of an acoustic source can be achieved by using a simple thresholding.
, respectively. Figure 14(a) shows the two distributions obtained from the data set collected in the DMN case when using the GCF map. The two distributions are clearly distinct and the detection of the presence of an acoustic source can be achieved by using a simple thresholding.
(a) distribution of the acoustic map maximum peak with and without active sources. (b) distribution of the maximum the peak of the de-emphasized map when 1 and 2 sources are active: although the two distributions get closer, a distinction between one and two active speaker contexts is still feasible.
Once hypothesis  has been detected, we consider the peak of the de-emphasized map
has been detected, we consider the peak of the de-emphasized map  and define two new hypotheses:
and define two new hypotheses:  when a single source is active, and
when a single source is active, and  when two sources are simultaneously emitting sounds. Figure 14(b) shows the distribution of the peak of the de-emphasized map in the two cases. Here, the distributions overlap more than in Figure 14(a) but it is still possible to distinguish between
when two sources are simultaneously emitting sounds. Figure 14(b) shows the distribution of the peak of the de-emphasized map in the two cases. Here, the distributions overlap more than in Figure 14(a) but it is still possible to distinguish between  and
and  by thresholding the map peak. Moreover, the detection can be improved by jointly using the map peaks related to two adjacent frames. In this case, other related investigations showed that the separability between
by thresholding the map peak. Moreover, the detection can be improved by jointly using the map peaks related to two adjacent frames. In this case, other related investigations showed that the separability between  and
and  increased if compared to a single frame based processing.
increased if compared to a single frame based processing.
To show this experimental evidence, a simple detection scheme was defined, based on a frame-by-frame analysis with fixed thresholding. The resulting system was evaluated in terms of false alarm and miss detection rates. Figure 15(a) reports the ROC (Receiver Operating Characteristic) curves related to the automatic discrimination between  and
and  while Figure 15(b) refers to
while Figure 15(b) refers to  and
and  . The figures show the detection performance obtained using the GCF peak of a single frame (label "Single") or of two consecutive frames (label "Double"). Experiments show that a ROC substantially lower than 0.1 is obtained to detect if at least one source is active. One can then distinguish between one and two active sources with a ROC less than 0.2 when using two frames. This fact suggests that multiple speaker activity detection algorithms based on GCF peak analysis performed on intervals of duration larger than two frames may provide a better result. Taking into account also the spatial distribution of the peaks, one can expect to further improve this performance.
. The figures show the detection performance obtained using the GCF peak of a single frame (label "Single") or of two consecutive frames (label "Double"). Experiments show that a ROC substantially lower than 0.1 is obtained to detect if at least one source is active. One can then distinguish between one and two active sources with a ROC less than 0.2 when using two frames. This fact suggests that multiple speaker activity detection algorithms based on GCF peak analysis performed on intervals of duration larger than two frames may provide a better result. Taking into account also the spatial distribution of the peaks, one can expect to further improve this performance.
6. Discussion and Future Work
This paper presented an algorithm for localization of multiple simultaneous sources through acoustic map analysis. The proposed approach has been successfully tested on real data sets collected by two different microphone settings.
Experiments show that different sensor deployments call for different parameter settings and hence an accurate selection of the de-emphasis function is needed to ensure satisfactory results. Therefore, the adoption of an adaptive de-emphasis depending on the relative positions of sources and microphones would probably help and will be investigated in the future.
The proposed method is suitable to be applied in a multi-source tracking framework, based on either Particle Filtering [27] or Kalman Filtering, since it ensures observation availability for all sources. Moreover, if tracking is employed, the de-emphasis function can be tailored to the hypothesized source positions.
The presented algorithm is also being integrated in audio-video tracking of multiple targets relying on a Bayesian framework [28]. Moreover, it has been used in the real-time DICIT prototype to track the position of two simultaneously active speakers while two loudspeakers (located at known positions) are reproducing stereo TV output.
The experimental work also shows that the main peaks of acoustic maps can be exploited to determine the number of active sources. Further analysis on this issue requires the introduction of these cues in a speech activity detection component. To this regard, several approaches can be followed, as, for instance, Random Finite Sets (RFS) that attempt to model death and birth of sources [29]. Other solutions may rely on short-term spatio-temporal clustering [5], which identifies the number of sources by clustering the localization estimates. Both methodologies will be addressed in future studies.
Finally, a further improvement can be achieved by exploiting some knowledge of the acoustic properties of the environment, in particular, for what concerns reverberation [24]. In this way, the early reflections associated to the dominant source could be properly handled, reducing their detrimental effects on the localization of the second source.
References
Brandstein M, Ward D: Microphone Arrays. Springer, New York, NY, USA; 2001.
Waibel A, Stiefelhagen R (Eds): Computers in the human interaction loop In Human Computer Interaction. Springer, New York, NY, USA; 2009.
Knapp CH, Carter GC: The generalized correlation method for estimation of time delay. IEEE Transactions on Acoustics, Speech, and Signal Processing 1976, 24: 320-327. 10.1109/TASSP.1976.1162830
Omologo M, Svaizer P: Acoustic event localization using a crosspower-spectrum based technique. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '94), 1994, Adelaide, Australia 2: 273-276.
Di Claudio ED, Parisi R, Orlandi G: Multi-source localization in reverberant environments by root-music and clustering. Proceedings of the IEEE Interntional Conference on Acoustics, Speech, and Signal Processing, June 2000 921-924.
Lathoud G, Odobez JM: Short-term spatio-temporal clustering applied to multiple moving speakers. IEEE Transactions on Audio, Speech and Language Processing 2007, 15(5):1696-1710.
Vermaak J, Blake A: Nonlinear filtering for speaker tracking in noisy and reverberant environments. Proceedings of the IEEE Interntional Conference on Acoustics, Speech, and Signal Processing, 2001 3021-3024.
Fallon M, Godsill S: Multi target acoustic source tracking with an unknown and time varying number of targets. Proceedings of the Hands-Free Speech Communication and Microphone Arrays (HSCMA '08), 2008 77-80.
Lee Y, Wada TS, Juang B-H: Multiple acoustic source localization based on multiple hypotheses testing using particle approach. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '10), 2010, Dallas, Tex, USA 2722-2725.
Bechler D, Kroschel K: Considering the second peak in the gcc function for multi-source tdoa estimation with microphone array. Proceedings of the International Workshop on Acoustic Echo and Noise Control, 2003, Kyoto, Japan 315-318.
Potamitis I, Chen H, Tremoulis G: Tracking of multiple moving speakers with multiple microphone arrays. IEEE Transactions on Speech and Audio Processing 2004, 12(5):520-529. 10.1109/TSA.2004.833004
Valin J-M, Michaud F, Hadjou B, Rouat J: Localization of simultaneous moving sound sources for mobile robot using a frequency-domain steered beamformer approach. Proceedings of the IEEE International Conference on Robotics and Automation, 2004 2004(1):1033-1038.
Pertilä P, Hämäläinen MS: A Track before detect approach for sequential bayesian tracking of multiple speech sources. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '10), 2010, Dallas, Tex, USA 4974-4977.
Madhu N, Martin R: A scalable framework for multiple speaker localization and tracking. Proceedings of the International Workshop on Acoustic Echo and Noise Control, 2008, Seattle, Wash, USA
Teng P, Lombard A, Kellermann W: Disambiguation in multidimensional tracking of multiple acoustic sources using a gaussian likelihood criterion. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '10), 2010, Dallas, Tex, USA 145-148.
Brutti A, Omologo M, Svaizer P: Localization of multiple speakers based on a two step acoustic map analysis. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '08), 2008, Las Vegas, Nev, USA 4349-4352.
Rabinkin DV, Renomeron RJ, Dahl A, French JC, Flanagan JL: A DSP implementation of source location using microphone arrays. Proceedings of the 131st Meeting of the Acoustical Society of America, 1996, Indianapolis, Ind, USA 88-99.
DeMori R (Ed): Spoken Dialogue with Computers. Academic Press, London, UK; 1998.
Lathoud G, Magimai-Doss M: A sector-based, frequency-domain approach to detection and localization of multiple speakers. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '05), 2005, Philadelphia, Pa, USA 265-268.
Griebel SM: A microphone array system for speech source localization, denoising and dereverberation, Ph.D. thesis. Harvard University; 2002.
Pertilä P, Korhonen T, Visa A: Measurement combination for acoustic source localization in a room environment. EURASIP Journal on Audio, Speech, and Music Processing vol 2008, Article ID 278185 14 pages 2008:.
Brutti A, Omologo M, Svaizer P: Oriented global coherence field for the estimation of the head orientation in smart rooms equipped with distributed microphone arrays. Proceedings of the 9th European Conference on Speech Communication and Technology, 2005 2337-2340.
Brutti A: Distributed microphone networks for sound source localization in smart rooms, Ph.D. thesis. University of Trento; 2007.
Svaizer P, Brutti A, Omologo M: Analysis of reflected wavefronts by means of a line microphone array. Proceedings of the International Workshop on Acoustic Echo and Noise Control, 2010, Tel Aviv, Israel
Ramírez J, Segura JC, Benítez C, De la Torre Á, Rubio A: Efficient voice activity detection algorithms using long-term speech information. Speech Communication 2004, 42(3-4):271-287. 10.1016/j.specom.2003.10.002
Fukuda T, Ichikawa O, Nishimura M: Long-term spectro-temporal and static harmonic features for voice activity detection. IEEE Journal on Selected Topics in Signal Processing 2010, 4(5):834-844.
Brutti A, Omologo M, Svaizer P: A sequential Monte Carlo approach for tracking of overlapping acoustic sources. Proceedings of the European Signal Processing Conference (EUSIPCO '09), 2009, Glasgow, UK 2559-2563.
Lanz O: Approximate Bayesian multibody tracking. IEEE Transactions on Pattern Analysis and Machine Intelligence 2006, 28(9):1436-1449.
Goutsias J, Mahler R, Nguyen H: Random Sets Theory and Applications. Springer, New York, NY, USA; 1997.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Brutti, A., Omologo, M. & Svaizer, P. Multiple Source Localization Based on Acoustic Map De-Emphasis. J AUDIO SPEECH MUSIC PROC. 2010, 147495 (2010). https://doi.org/10.1155/2010/147495
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/147495




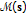 based on (3), (4) or (7), take the coordinates
based on (3), (4) or (7), take the coordinates  of the map maximum as estimate of the dominant source position (the position of the peak may be derived from the current observations only, or could result from a more articulated tracking algorithm),
of the map maximum as estimate of the dominant source position (the position of the peak may be derived from the current observations only, or could result from a more articulated tracking algorithm), , derive a new GCC-PHAT function
, derive a new GCC-PHAT function 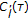 by reducing the magnitude of the original function
by reducing the magnitude of the original function  for
for  close to
close to  ,
,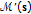 using the
using the 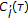 functions,
functions, and take its coordinates
and take its coordinates  as estimate of the lower-rank source position.
as estimate of the lower-rank source position.





 computed on average over all combinations in the DMN scenario. Three acoustic maps are reported: GCF, M-OGCF, and LS. (d) refers to the specific case P1-P3 and GCF map.
computed on average over all combinations in the DMN scenario. Three acoustic maps are reported: GCF, M-OGCF, and LS. (d) refers to the specific case P1-P3 and GCF map.


 computed over all combinations in the linear array configuration.
computed over all combinations in the linear array configuration.

