- Research Article
- Open access
- Published:
Measurement Combination for Acoustic Source Localization in a Room Environment
EURASIP Journal on Audio, Speech, and Music Processing volume 2008, Article number: 278185 (2008)
Abstract
The behavior of time delay estimation (TDE) is well understood and therefore attractive to apply in acoustic source localization (ASL). A time delay between microphones maps into a hyperbola. Furthermore, the likelihoods for different time delays are mapped into a set of weighted nonoverlapping hyperbolae in the spatial domain. Combining TDE functions from several microphone pairs results in a spatial likelihood function (SLF) which is a combination of sets of weighted hyperbolae. Traditionally, the maximum SLF point is considered as the source location but is corrupted by reverberation and noise. Particle filters utilize past source information to improve localization performance in such environments. However, uncertainty exists on how to combine the TDE functions. Results from simulated dialogues in various conditions favor TDE combination using intersection-based methods over union. The real-data dialogue results agree with the simulations, showing a 45% RMSE reduction when choosing the intersection over union of TDE functions.
1. Introduction
Passive acoustic source localization (ASL) methods are attractive for surveillance applications, which are a constant topic of interest. Another popular application is human interaction analysis in smart rooms with multimodal sensors. Automating the perception of human activities is a popular research topic also approached from the aspect of localization. Large databases of smart room recordings are available for system evaluations and development [1]. A typical ASL system consists of several spatially separated microphones. The ASL output is either source direction or location in two- or three-dimensional space, which is achieved by utilizing received signal phase information [2] and/or amplitude [3], and possibly sequential information through tracking [4].
Traditional localization methods maximize a spatial likelihood function (SLF) [5] to locate the source. Localization methods can be divided according to the way the spatial likelihood is formed at each time step. The steered beamforming approach sums delayed microphone signals and calculates the output power for a hypothetical location. It is therefore a direct localization method, since microphone signals are directly applied to build the SLF.
Time delay estimation (TDE) is widely studied and well understood and therefore attractive to apply in the source localization problem. The behavior of correlation-based TDE methods has been studied theoretically [6] also in reverberant enclosures [7, 8]. Other TDE approaches include determining adaptively the transfer function between microphone channels [9], or the impulse responses between the source and receivers [10]. For more discussion on TDE methods, see [11].
TDE-based localization methods first transform microphone pair signals into a time delay likelihood function. These pairwise likelihood functions are then combined to construct the spatial likelihood function. It is therefore a two-step localization approach in comparison to the direct approach. The TDE function provides a likelihood for any time delay value. For this purpose, the correlation-based TDE methods are directly applicable. A hypothetical source position maps into a time delay between a microphone pair. Since the TDE function assigns a likelihood for the time delay, the likelihood for the hypothetical source position is obtained. From a geometrical aspect, time delay is inverse-mapped as a hyperbola in 3D space. Therefore, the TDE function corresponds to a set of weighted nonoverlapping hyperbolae in the spatial domain. The source location can be solved by utilizing spatially separated microphone pairs, that is, combining pairwise TDE functions to construct a spatial likelihood function (SLF). The combination method varies. Summation is used in [12–14], multiplication is used in [15, 16], and the determinant, used originally to determine the time delay from multiple microphones in [17], can also be applied for TDE function combination in localization. The traditional localization methods consider the maximum point of the most recent SLF as the source location estimate. However, in a reverberant and noisy environment, the SLF can have peaks outside the source position. Even a moderate increase in the reverberation time may cause dominant noise peaks [7], leading to the failure of the traditional localization approach [15]. Recently, particle filtering (PF)-based sound source localization systems have been presented [13, 15, 16, 18]. This scheme uses information also from the past time frames to estimate the current source location. The key idea is that spatially inconsistent dominant noise peaks in the current SLF do not necessarily corrupt the location estimate. This scheme has been shown to extend the conditions in which an ASL system is usable in terms of signal to noise ratio (SNR) and reverberation time (T60) compared to the traditional approach [15].
As noted, several ways of combination TDE functions have been used in the past, and some uncertainty exists about a suitable method for building the SLF for sequential 3D source localization. To address this issue, this work introduces a generalized framework for combining TDE functions in TDE-based localization using particle filtering. Geometrically, the summation of TDE functions represents the union of pairwise spatial likelihoods, that is, union of the sets of weighted hyperbolae. Such SLF does have the maximum value at the correct location but also includes the unnecessary tails of the hyperbolae. Taking the intersection of the sets reduces the unnecessary tails of the hyperbolae, that is, acknowledges that the time delay is eventually related only to a single point in space and not to the entire set of points it gets mapped into (hyperbola). TDE combination schemes are compared using a simulated dialogue. The simulation reverberation time (T60) ranges from 0 to 0.9 second, and the SNR ranges from  to
to  dB. Also real-data from a dialogue session is examined in detail.
dB. Also real-data from a dialogue session is examined in detail.
The rest of this article is organized as follows: Section 2 discusses the signal model and TDE functions along with signal parameters that affect TDE. Section 3 proposes a general framework for combining the TDE functions to build the SLF. Section 4 categorizes localization methods based on the TDE combination operation they apply and discusses how the combination affects the SLF shape. Iterative localization methods are briefly discussed. Particle filtering theory is reviewed in Section 5 for sequential SLF estimation and localization. In Section 6, simulations and real-data measurements are described. Selected localization methods are compared in Section 7. Finally, Sections 8 and 9 conclude the discussion.
2. Signal Model and TDE Function
The sound signal emitted from a source is propagated into the receiving microphone. The received signal is a convolution of source signal and an impulse response. The impulse response encompasses the measurement equipment response, room geometry, materials as well as the propagation delay from a source  to a microphone
to a microphone  and reverberation effects. The
and reverberation effects. The  th microphone signal is a superposition of convoluted source signals [14, 15]:
th microphone signal is a superposition of convoluted source signals [14, 15]:

where  , and
, and  is the signal emitted by the
is the signal emitted by the  th source,
th source,  ,
,  is assumed here to be independent and identically distributed noise,
is assumed here to be independent and identically distributed noise,  represents discrete time index,
represents discrete time index,  is the impulse response, and
is the impulse response, and  denotes convolution. The propagation time from a source point
denotes convolution. The propagation time from a source point  to microphone
to microphone  is
is

where  is the speed of sound, and
is the speed of sound, and  is the Euclidean norm. Figure 1(a) illustrates propagation delay from source to microphones, using a 2D simplification.
is the Euclidean norm. Figure 1(a) illustrates propagation delay from source to microphones, using a 2D simplification.
Source localization geometry is presented. The sampling frequency is  , the speed of sound is
, the speed of sound is  , the source signal is colored noise, and SNR is
, the source signal is colored noise, and SNR is  . The sources are located at
. The sources are located at  and
and  or at TDOA values
or at TDOA values  and
and  . In panel (a), the propagation time from source at
. In panel (a), the propagation time from source at  is different for the two microphones (values given in samples). This difference is the TDOA value of the source. Panel (b) illustrates how different TDOA values are mapped into hyperbolae. In panel (c), the two peaks at locations
is different for the two microphones (values given in samples). This difference is the TDOA value of the source. Panel (b) illustrates how different TDOA values are mapped into hyperbolae. In panel (c), the two peaks at locations  and
and  in the TDE function correspond to the source locations
in the TDE function correspond to the source locations  and
and  , respectively. Panel (d) displays the TDE function values from panel (c) mapped into a microphone pairwise spatial likelihood function (SLF).Propagation delay from source 1TDOA values and corresponding hyperbolaeTDE function values,
, respectively. Panel (d) displays the TDE function values from panel (c) mapped into a microphone pairwise spatial likelihood function (SLF).Propagation delay from source 1TDOA values and corresponding hyperbolaeTDE function values,  Spatial likelihood function (SLF) for a microphone pair
Spatial likelihood function (SLF) for a microphone pair
A wavefront emitted from point  arrives at spatially separated microphones
arrives at spatially separated microphones  according to their corresponding distance from point
according to their corresponding distance from point  . This time difference of arrival (TDOA) value between the pair
. This time difference of arrival (TDOA) value between the pair  in samples is [14]
in samples is [14]

where  is the sampling frequency, and
is the sampling frequency, and  denotes rounding. Conversely, a delay between microphone pair
denotes rounding. Conversely, a delay between microphone pair  defines a set of 3D locations
defines a set of 3D locations  forming a hyperbolic surface that includes the unique location
forming a hyperbolic surface that includes the unique location  . The geometry is illustrated in Figure 1(b), where hyperbolae related to TDOA values
. The geometry is illustrated in Figure 1(b), where hyperbolae related to TDOA values  are illustrated.
are illustrated.
In this work, a TDE function between microphone pair  is defined
is defined  , where the delay can have values:
, where the delay can have values:


The unit of delay is one sample. TDE functions include the generalized cross correlation (GCC) [19] which is defined for a frame of microphone pair  data:
data:

where  is a complex conjugate transpose of the DFT of the
is a complex conjugate transpose of the DFT of the  th microphone signal,
th microphone signal,  is discrete frequency,
is discrete frequency,  denotes inverse DFT, and
denotes inverse DFT, and  is a weighting function, see [19]. Phase transform (PHAT) weighting
is a weighting function, see [19]. Phase transform (PHAT) weighting  causes sharper peaks in the TDE function compared to the nonweighted GCC and is used by several TDE-based localization methods, including the steered response power using phase transform (SRP-PHAT) [14]. An example of TDE function is displayed in Figure 1(c). Other weighting schemes include the Roth, Scot, Eckart, the Hannan-Thomson (maximum likelihood) [19], and the Hassab-Boucher methods [20].
causes sharper peaks in the TDE function compared to the nonweighted GCC and is used by several TDE-based localization methods, including the steered response power using phase transform (SRP-PHAT) [14]. An example of TDE function is displayed in Figure 1(c). Other weighting schemes include the Roth, Scot, Eckart, the Hannan-Thomson (maximum likelihood) [19], and the Hassab-Boucher methods [20].
Other applicable TDE functions include the modified average magnitude difference function (MAMDF) [21]. Recently, time frequency histograms have been proposed to increase TDE robustness against noise [22]. For a more detailed discussion on TDE refer to [11]. The evaluation of different TDE methods and GCC weighting methods is, however, outside the scope of this work. Hereafter, the PHAT-weighted GCC is utilized as the TDE weighting function since it is the optimal weighting function for a TDOA estimator in a reverberant environment [8].
The correlation-based TDOA is defined as the peak location of the GCC-based TDE function [19]. Three distinct SNR ranges (high, low, and the transition range in between) in TDOA estimation accuracy have been identified in a nonreverberant environment [6]. In the high SNR range, the TDOA variance attains the Cramer-Rao lower bound (CRLB) [6]. In the low SNR range, the TDE function is dominated by noise, and the peak location is noninformative. In the transition range, the TDE peak becomes ambiguous and is not necessary related to the correct TDOA value. TDOA estimators fail rapidly when the SNR drops into this transition SNR range [6]. According to the modified Ziv-Zakai lower bound, this behavior depends on time-bandwidth product, bandwidth to center frequency ratio, and SNR [6]. In addition, the CRLB depends on the center frequency.
In a reverberant environment the correlation-based TDOA performance is known to rapidly decay when the reverberation time (T60) increases [7]. The CRLB of the correlation-based TDOA estimator in the reverberant case is derived in [8] where PHAT weighting is shown to be optimal. In that model, the signal to noise and reverberation ratio (SNRR) and signal frequency band affect the achievable minimum variance. The SNRR is a function of the acoustic reflection coefficient, noise variance, microphone distance from the source, and the room surface area.
3. Framework for Building the Spatial Likelihood Function
Selecting a spatial coordinate  assigns a microphone pair
assigns a microphone pair  with a TDOA value
with a TDOA value  as defined in (3). The TDE function (6) indexed with this value, that is,
as defined in (3). The TDE function (6) indexed with this value, that is,  , represents the likelihood of the source existing at the locations that are specified by the TDOA value, that is, hyperboloid
, represents the likelihood of the source existing at the locations that are specified by the TDOA value, that is, hyperboloid  . The pairwise SLF can be written as
. The pairwise SLF can be written as

where  represents conditional likelihood, normalized between
represents conditional likelihood, normalized between  . Figure 1(d) displays the pairwise SLF of the TDE measurement displayed in Figure 1(c). Equation (7) can be interpreted as a likelihood of a source having location
. Figure 1(d) displays the pairwise SLF of the TDE measurement displayed in Figure 1(c). Equation (7) can be interpreted as a likelihood of a source having location  given the measurement
given the measurement  .
.
The pairwise SLF consists of weighted nonoverlapping hyperbolic objects and therefore has no unique maximum. A practical solution to reduce the ambiguity of the maximum point is to utilize several microphone pairs. The combination operator used to perform fusion between these pairwise SLFs influences the shape of the resulting SLF. Everything else except the source position of each of the hyperboloid's shape is nuisance.
A binary operator combining two likelihoods can be defined as

Among such operators, ones that are commutative, monotonic, associative, and bounded between  are of interest here. For likelihoods A, B, C, D, these rules are written as
are of interest here. For likelihoods A, B, C, D, these rules are written as



Such operations include  -norm and
-norm and  -norm.
-norm.  -norm operations between two sets represent the union of sets and have the property
-norm operations between two sets represent the union of sets and have the property  . The most common
. The most common  -norm operation is summation. Other well- known
-norm operation is summation. Other well- known  -norm operations include the Euclidean distance and maximum value.
-norm operations include the Euclidean distance and maximum value.
A  -norm operation represents the intersection of sets and satisfies the property
-norm operation represents the intersection of sets and satisfies the property  . Multiplication is the most common such operation. Other
. Multiplication is the most common such operation. Other  -norm operations include the minimum value and Hamacher
-norm operations include the minimum value and Hamacher  -norm [23] which is a parameterized norm and is written for two values A and B:
-norm [23] which is a parameterized norm and is written for two values A and B:

where  is a parameter. Note that the multiplication is a special case of (12) when
is a parameter. Note that the multiplication is a special case of (12) when  .
.
Figure 2 illustrates the combination of two likelihood values, A and B. The likelihood values are displayed on the axes. The leftmost image represents summation, the middle represents product and the rightmost is Hamacher  -norm (
-norm ( ). The contour lines represent the joint likelihood. The summation is the only
). The contour lines represent the joint likelihood. The summation is the only  -norm here. In general, the
-norm here. In general, the  -norm is large only if all likelihoods are large. Similarly, the
-norm is large only if all likelihoods are large. Similarly, the  -norm can be large even if some likelihood values are small.
-norm can be large even if some likelihood values are small.
The combination of pairwise SLFs can be written: (using  with prefix notation.)
with prefix notation.)

where each microphone pair  belongs to a microphone pair group
belongs to a microphone pair group  , and
, and  represents all the TDE functions of the group. There exists
represents all the TDE functions of the group. There exists  unique microphone pairs in the set of all pairs. Sometimes partitioning the set of microphones into groups or arrays before pairing is justified. The signal coherence between two microphones decreases as microphone distance increases [24] which favors partitioning the microphones into groups with low sensor distance. Also, the complexity of calculating all pairwise TDE function values is
unique microphone pairs in the set of all pairs. Sometimes partitioning the set of microphones into groups or arrays before pairing is justified. The signal coherence between two microphones decreases as microphone distance increases [24] which favors partitioning the microphones into groups with low sensor distance. Also, the complexity of calculating all pairwise TDE function values is  , which is lower for partitioned arrays. Selecting too small sensor separation may lead to over-quantization of the possible TDOA values where only a few delay values exist, see (5).
, which is lower for partitioned arrays. Selecting too small sensor separation may lead to over-quantization of the possible TDOA values where only a few delay values exist, see (5).
4. TDE-Based Localization Methods
Several TDE-based combination schemes exist in the ASL literature. The most common method is the summation. This section presents four distinct operations in the generalized framework.
4.1. Summation Operator in TDE-Based Localization
The method in [12] sums GCC values, which is equivalent to the steered beamformer. The method in [13] sums precedence-weighted GCC values (for direction estimation). SRP-PHAT method sums PHAT-weighted GCC values [14]. All these methods use the summation operation which fulfills the requirements (9)–(11). Using (13), the SRP-PHAT is written as

Every high value of the pairwise SLF is present in the resulting SLF since the sum represents a union of values. In a multiple source situation with more than two sensors, this approach generates high probability regions outside actual source positions, that is, ghosts. See Figure 3(a) for illustration, where ghosts appear, for example, at x, y coordinates  and
and  .
.
A two-source example scenario with three microphone pairs is illustrated. The source coordinates are  and
and  . Two combination operators sum and product are used to produce two separate spatial likelihood functions (SLFs). The SLF contours are presented in panels (d) and (h). Circle and square represent microphone and source locations, respectively. Panels (a) and (e) illustrate the resulting 2D SLF, produced with the sum and product operations, respectively. The marginal distributions of the SLFs are presented in panels (b) and (c) for the sum, and (f) and (g) for the product. The panel (a) distribution has ghosts which are the result of summed observations, see example ghost at
. Two combination operators sum and product are used to produce two separate spatial likelihood functions (SLFs). The SLF contours are presented in panels (d) and (h). Circle and square represent microphone and source locations, respectively. Panels (a) and (e) illustrate the resulting 2D SLF, produced with the sum and product operations, respectively. The marginal distributions of the SLFs are presented in panels (b) and (c) for the sum, and (f) and (g) for the product. The panel (a) distribution has ghosts which are the result of summed observations, see example ghost at  . Also, the marginal distributions are not informative. In the panel (e), SLF has sharp peaks which are in the presence of the actual sound sources. The marginal distributions carry source position information, though this is not guaranteed in general.
. Also, the marginal distributions are not informative. In the panel (e), SLF has sharp peaks which are in the presence of the actual sound sources. The marginal distributions carry source position information, though this is not guaranteed in general.
4.2. Multiplication Operator in TDE-Based Localization
In [15, 16], product was used as the likelihood combination operator which is a probabilistic approach. (In [15] negative GCC values are clipped and the resulting positive values are raised to power  ) If the likelihoods are independent, the intersection of sets equals their product. The method, termed here multi-PHAT, multiplies the pairwise PHAT-weighted GCC values together in contrast to summation. The multi-PHAT fulfills (9)–(11) and is written using (13)
) If the likelihoods are independent, the intersection of sets equals their product. The method, termed here multi-PHAT, multiplies the pairwise PHAT-weighted GCC values together in contrast to summation. The multi-PHAT fulfills (9)–(11) and is written using (13)

This approach outputs the common high likelihood areas of the measurements, and so the unnecessary peaks of the SLF are somewhat reduced. The ghosts experienced in the SRP-PHAT method are eliminated in theory by the intersection-based combination approach. This is illustrated in Figure 3(b). The SLF has two distinct peaks that correspond to the true source locations.
4.3. Hamacher -Norm in TDE-Based Localization
Several other methods that have the properties (9)–(11) can be used to combine likelihoods. These methods include parameterized  -norms and
-norms and  -norms [23]. Here, the Hamacher
-norms [23]. Here, the Hamacher  -norm (12) is chosen because it is relatively close to the product and represents the intersection of sets. The Hamacher
-norm (12) is chosen because it is relatively close to the product and represents the intersection of sets. The Hamacher  -norm is defined as a dual norm, since it operates on two inputs.
-norm is defined as a dual norm, since it operates on two inputs.
The parameter  in the Hamacher
in the Hamacher  -norm (12) defines how the norm behaves. For example,
-norm (12) defines how the norm behaves. For example,  whereas their product equals
whereas their product equals  , and
, and  . Figures 2(b) and 2(c) represent the multiplication and Hamacher
. Figures 2(b) and 2(c) represent the multiplication and Hamacher  -norm (
-norm ( ). The Hamacher
). The Hamacher  -norm-based TDE localization method is written using (13):
-norm-based TDE localization method is written using (13):

where  is abbreviated notation of
is abbreviated notation of  , that is, the PHAT-weighted GCC value from the
, that is, the PHAT-weighted GCC value from the  th microphone pair for location
th microphone pair for location  , where
, where  is the total number of pairs, and
is the total number of pairs, and  is the Hamacher
is the Hamacher  -norm (12). Since the norm is commutative, the TDE measurements can be combined in an arbitrary order. Any positive
-norm (12). Since the norm is commutative, the TDE measurements can be combined in an arbitrary order. Any positive  value can be chosen, but values
value can be chosen, but values  were empirically found to produce good results. Note that multi-PHAT is a special case of Hamacher-PHAT when
were empirically found to produce good results. Note that multi-PHAT is a special case of Hamacher-PHAT when  .
.
4.4. Other Combination Methods in TDE-Based Localization
Recently, a spatial correlation-based method for TDOA estimation has been proposed [17], termed the multichannel cross correlation coefficient (MCCC) method. It combines cross correlation values for TDOA estimation and is considered here for localization. The correlation matrix from a  microphone array is here written:
microphone array is here written:

where  equals
equals  . In [17], the matrix (17) is used for TDOA estimation, but here it is interpreted as a function of source position using (13)
. In [17], the matrix (17) is used for TDOA estimation, but here it is interpreted as a function of source position using (13)

The spatial likelihood of, for example, a three microphone array is

The MCCC method is argued to remove the effect of a channel that does not correlate with the other channels [17]. This method does not satisfy the monotonicity assumption (10). Also, the associativity (11) does not follow in arrays larger than three microphones.
4.5. Summary of the TDE Combination Methods
Four different TDE combination schemes were discussed, and existing localization methods were categorized accordingly. Figure 3 displays the difference between the intersection and the union of TDE function in localization. The SLF produced with the Hamacher  -norm differs slightly from the multiplication approach and is not illustrated. Also, the SLF produced with the MCCC is relatively close to the summation, as seen later in Figure 10. The intersection results in the source location information. The union contains the same information as the intersection but also other regions, such as the tails of the hyperbolae. This extra information does not help localization. In fact, likelihood mass outside true source position increases the estimator variance. However, this extra likelihood mass can be considered in other applications, for example, to determine the speaker's head orientation [25].
-norm differs slightly from the multiplication approach and is not illustrated. Also, the SLF produced with the MCCC is relatively close to the summation, as seen later in Figure 10. The intersection results in the source location information. The union contains the same information as the intersection but also other regions, such as the tails of the hyperbolae. This extra information does not help localization. In fact, likelihood mass outside true source position increases the estimator variance. However, this extra likelihood mass can be considered in other applications, for example, to determine the speaker's head orientation [25].
4.6. Iterative Methods for TDE-Based Source Location Estimation
A straightforward but computationally expensive approach for source localization is to exhaustively find the maximum value of the SLF. The SRP-PHAT is perhaps the most common way of building the SLF so a lot of algorithms, including the following ones, have been developed to reduce the computational burden. A stochastic [26] and a deterministic [27] ways of reducing the number of SLF evaluations have been presented. These methods iteratively reduce the search volume that contains the maximum point until the volume is small enough. In [28], the fact that a time delay is inverse-mapped into multiple spatial coordinates was utilized to reduce the number of SLF grid evaluations by considering only the neighborhood of the  highest TDE function values. In [29], the SLF is maximized initially at low frequencies that correspond to large spatial blocks. The maximum-valued SLF block is selected and further divided into smaller blocks by increasing the frequency range. The process is repeated until a desired accuracy is reached.
highest TDE function values. In [29], the SLF is maximized initially at low frequencies that correspond to large spatial blocks. The maximum-valued SLF block is selected and further divided into smaller blocks by increasing the frequency range. The process is repeated until a desired accuracy is reached.
5. Sequential Spatial Likelihood Estimation
In the Bayesian framework, the SLF represents the noisy measurement distribution  at time frame
at time frame  , where
, where  represents measurement and
represents measurement and  state. In the previous section, several means of building the measurement distribution were discussed. The next step is to estimate the source position using the posterior distribution
state. In the previous section, several means of building the measurement distribution were discussed. The next step is to estimate the source position using the posterior distribution  . The subindices emphasize that the distribution includes all the previous measurements and state information, unlike the iterative methods discussed above. The state
. The subindices emphasize that the distribution includes all the previous measurements and state information, unlike the iterative methods discussed above. The state  represents a priori information. The first measurement is available at time frame
represents a priori information. The first measurement is available at time frame  = 1.
= 1.
It is possible to estimate the posterior distribution in a recursive manner [4]. This can be done in two steps, termed prediction and update. The prediction of the state distribution is calculated by convolving the posterior distribution with a transition distribution  written as
written as

The new SLF, that is,  is used to correct the prediction distribution:
is used to correct the prediction distribution:

where the nominator is a normalizing constant. For each time frame  the two steps (20) and (21) are repeated.
the two steps (20) and (21) are repeated.
In this work, a particle filtering method is used to numerically estimate the integrals involved [4, 30]. For a tutorial on PF methods, refer to [30]. PF approximates the posterior density with a set of  weighted random samples
weighted random samples  for each frame
for each frame  . The approximate posterior density is written as
. The approximate posterior density is written as

where the scalar weights  sum to unity, and
sum to unity, and  is the Dirac's delta function.
is the Dirac's delta function.
In this work, the particles  are 3D points in space. The specific PF method used is the sampling importance resampling (SIR), described in Algorithm 1. The algorithm propagates the particles according to the motion model which is here selected as a dual-Gaussian distribution (Brownian motion). Both distributions are centered on the current estimate with standard deviations of
are 3D points in space. The specific PF method used is the sampling importance resampling (SIR), described in Algorithm 1. The algorithm propagates the particles according to the motion model which is here selected as a dual-Gaussian distribution (Brownian motion). Both distributions are centered on the current estimate with standard deviations of  and
and  , (see Algorithm 1 Line 3). The new weights are calculated from the SLF on Line 4.
, (see Algorithm 1 Line 3). The new weights are calculated from the SLF on Line 4.
Algorithm 1: SIR algorithm for particle filtering [30].
-
1
 = SIR
= SIR 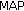 ;
; -
2
for
 to
to
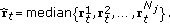 do
do
3  ;
;
4 Calculate  ;
;
-
5
end
-
6
Normalize weights,
 ;
; -
7
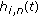 = RESAMPLE
= RESAMPLE  ;
;
The resampling is applied to avoid the degeneracy problem, where all but one particle have insignificant weight. In the resampling step, particles of low weight are replaced with particles of higher weight. In addition, a percentage of the particles are randomly distributed inside the room to notice events like the change of the active speaker. After estimating the posterior distribution, a point estimate is selected to represent the source position. Point estimation methods include the maximum a posteriori ( ), the conditional mean (
), the conditional mean ( ), and the median particle. If the SLF is multimodal,
), and the median particle. If the SLF is multimodal,  will be in the center of the mass and thus not necessarily near any source. In contrast,
will be in the center of the mass and thus not necessarily near any source. In contrast,  and median will be inside a mode. Due to the large number of particles, the median is less likely to oscillate between different modes than
and median will be inside a mode. Due to the large number of particles, the median is less likely to oscillate between different modes than  . In SIR, the
. In SIR, the  would be the maximum weighted particle from the SLF and thus prone to spurious peaks. Also, the
would be the maximum weighted particle from the SLF and thus prone to spurious peaks. Also, the  cannot be taken after the resampling step since the weights are effectively equal. Therefore, the median is selected as the source state estimate:
cannot be taken after the resampling step since the weights are effectively equal. Therefore, the median is selected as the source state estimate:

6. Simulation and Recording Setup
A dialogue situation between talkers is analyzed. The localization methods already discussed are compared using simulations and real-data measurements performed in a room environment. The simulation is used to analyze how the different TDE combination methods affect the estimation performance when noise and reverberation are added. The real-data measurements are used to verify the performance difference.
The meeting room dimensions are 4.53  3.96
3.96  2.59 m. The room layout and talker locations are illustrated in Figure 4. The room contains three identical microphone arrays. Each array consists of four microphones, and their coordinates are given in Table 1. The real room is additionally equipped with furniture and other small objects.
2.59 m. The room layout and talker locations are illustrated in Figure 4. The room contains three identical microphone arrays. Each array consists of four microphones, and their coordinates are given in Table 1. The real room is additionally equipped with furniture and other small objects.
6.1. Real-Data Measurements
The measured reverberation time T60 of the meeting room is 0.25 seconds, obtained with the maximum-length sequence (MLS) technique [31] using the array microphones and a loudspeaker. A sampling rate of 44.1 kHz is used, with 24 bits per sample, stored in linear PCM format. The array microphones are Sennheiser MKE 2-P-C electret condenser microphones with a 48 V phantom feed.
A 26 second dialogue between human talkers was recorded. The talkers uttered a predefined Finnish sentence and repeated the sentence in turns for six times. The SNR is estimated to be at least 16 dB in each microphone. The recording signal was manually annotated into three different classes "talker 1", "talker 2", and "silence". Figure 5 displays the signal and its annotation. The reference position is measured from the talker's lips and contains some errors due to unintentional movement of the talker and the practical nature of the measurement.
6.2. Simulations
The meeting room is simulated using the image method [32]. The method estimates the impulse response  between the source
between the source  and receiving microphone
and receiving microphone  . The resulting microphone signal is calculated using (1). The reverberation time (T60) of the room is varied by changing the reflection coefficient of the walls
. The resulting microphone signal is calculated using (1). The reverberation time (T60) of the room is varied by changing the reflection coefficient of the walls  , and the ceiling and floor
, and the ceiling and floor  which are related by
which are related by  . The coefficient determines the amount of sound energy reflected from a surface. Recordings with 10 different T60 values between 0 and 0.9 second are simulated with SNR ranging from
. The coefficient determines the amount of sound energy reflected from a surface. Recordings with 10 different T60 values between 0 and 0.9 second are simulated with SNR ranging from  dB to
dB to  dB in 0.8 dB steps for each T60 value. The simulation signals consisted of 4 seconds of recorded babble. The active talker switches from talker 1 to talker 2 at time 2.0 seconds. The total number of recordings is 510. The T60 values are [0, 0.094, 0.107, 0.203, 0.298, 0.410, 0.512, 0.623, 0.743, 0.880]. These are median values of channel T60 values calculated from the impulse response using Schroeder integration [33].
dB in 0.8 dB steps for each T60 value. The simulation signals consisted of 4 seconds of recorded babble. The active talker switches from talker 1 to talker 2 at time 2.0 seconds. The total number of recordings is 510. The T60 values are [0, 0.094, 0.107, 0.203, 0.298, 0.410, 0.512, 0.623, 0.743, 0.880]. These are median values of channel T60 values calculated from the impulse response using Schroeder integration [33].
7. Localization System Framework
The utilized localization system is based on the ASL framework discussed in this work. Microphone pairwise TDE functions are calculated inside each array with GCC-PHAT [19]. Pairwise GCC values are normalized between [0,1] by first subtracting the minimum value and dividing by the largest such GCC value of the array. A Hamming windowed frame of size 1024 samples is utilized (23.2 milliseconds) with no overlapping between sequential frames. The microphones are grouped into three arrays, and each array contains four microphones, see Table 1. Six unique pairs inside each array are utilized. Microphone pairs between the arrays are not included in order to lessen the computational complexity. The TDE function values are combined with the following schemes, which are considered for ASL:
(1)SRP-PHAT  PF: PHAT-weighted GCC values are summed to form the SLF (14), and SIR-PF algorithm is applied.
PF: PHAT-weighted GCC values are summed to form the SLF (14), and SIR-PF algorithm is applied.
(2)Multi-PHAT  PF: PHAT-weighted GCC values are multiplied together to form the SLF (15), and SIR-PF algorithm is applied.
PF: PHAT-weighted GCC values are multiplied together to form the SLF (15), and SIR-PF algorithm is applied.
-
(3)
Hamacher-PHAT
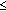 PF: PHAT-weighted GCC values are combined pairwise using the Hamacher
PF: PHAT-weighted GCC values are combined pairwise using the Hamacher 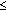 -norm (16), with parameter value
-norm (16), with parameter value  . The SIR-PF algorithm is then applied.
. The SIR-PF algorithm is then applied.
(4)MCCC  PF: PHAT-weighted GCC values are formed into a matrix (17), and the determinant operator is used to combine the pairwise array TDE functions (18). Multiplication is used to combine the resulting three array likelihoods together. In the simulation, multiplication produced better results than using the determinant operator for the array likelihoods. The SIR-PF algorithm is also applied.
PF: PHAT-weighted GCC values are formed into a matrix (17), and the determinant operator is used to combine the pairwise array TDE functions (18). Multiplication is used to combine the resulting three array likelihoods together. In the simulation, multiplication produced better results than using the determinant operator for the array likelihoods. The SIR-PF algorithm is also applied.
The particle filtering algorithm discussed in Section 5 (SIR-PF) is used with 5000 particles. The systematic resampling was applied due to its favorable resampling quality and low computational complexity [34]. The particles are confined to room dimensions and in the real-data analysis also between heights of 0.5–1.5 m to reduce the effects of ventilation noise. The 5000 particles have a Brownian motion model, with empirically chosen standard deviation  values 0.05 and 0.01 m for the simulations and real-data experiments, respectively. The Brownian motion model was selected since the talkers are somewhat stationary. Different dynamic models could be applied if the talkers move [35].The particles are uniformly distributed inside the room at the beginning of each run, that is, the a priori spatial likelihood function is uniform.
values 0.05 and 0.01 m for the simulations and real-data experiments, respectively. The Brownian motion model was selected since the talkers are somewhat stationary. Different dynamic models could be applied if the talkers move [35].The particles are uniformly distributed inside the room at the beginning of each run, that is, the a priori spatial likelihood function is uniform.
7.1. Estimator Performance
The errors are measured in terms of root mean square (RMS) values of the 3D distance between the point estimate  and reference position
and reference position  . The RMS error of an estimator is defined as
. The RMS error of an estimator is defined as

where  is the frame index, and
is the frame index, and  represents the number of frames.
represents the number of frames.
In the real-data analysis, the time frames annotated as "silence" are omitted. 0.3 second of data is omitted from the beginning of the simulation and after the speaker change to reduce the effects of particle filter convergence on the RMS error. Omitting of nonspeech frames could be performed automatically with a voice activity detector (VAD), see for example [36].
7.2. Results for Simulations
Results for the simulations using the four discussed ASL methods are given in Figures 6 and 7, for talker locations 1 and 2, respectively. The subfigures (a) to (d) represent the RMS error contours for each of the four methods. The x-axis displays the SNR of the recording, and y-axis displays the reverberation time (T60) value of the recording. A large RMS error value indicates that the method does not produce meaningful results.
The figure presents simulation results for talker location 1. The four ASL methods used are described in Section 7. The RMS error is defined in Section 7.1. The signals SNR values range from  to 30 dB, with reverberation time T60 between 0 and 0.9 second, see Section 6. The contour lines represent RMS error values at steps [0.2, 0.5] m.Method 1, SRP-PHAT
to 30 dB, with reverberation time T60 between 0 and 0.9 second, see Section 6. The contour lines represent RMS error values at steps [0.2, 0.5] m.Method 1, SRP-PHAT  PFMethod 2. Multi-PHAT
PFMethod 2. Multi-PHAT  PFMethod 3: Hamacher-PHAT
PFMethod 3: Hamacher-PHAT  PFMethod 4: MCCC-PHAT
PFMethod 4: MCCC-PHAT  PF
PF
The figure presents simulation results for talker location 2. The four ASL methods used are described in Section 7. The RMS error is defined in Section 7.1. The signals SNR values range from  to 30 dB, with reverberation time T60 between 0 and 0.9 second, see Section 6. The contour lines represent RMS error values at steps [0.2, 0.5] m.Method 1, SRP-PHAT
to 30 dB, with reverberation time T60 between 0 and 0.9 second, see Section 6. The contour lines represent RMS error values at steps [0.2, 0.5] m.Method 1, SRP-PHAT  PFMethod 2. Multi-PHAT
PFMethod 2. Multi-PHAT  PFMethod 3: Hamacher-PHAT
PFMethod 3: Hamacher-PHAT  PFMethod 4: MCCC-PHAT
PFMethod 4: MCCC-PHAT  PF
PF
For all methods, talker location 1 results in better ASL performance, than location 2. The results of location 1 are examined in detail.
The multi- and Hamacher-PHAT (intersection) methods clearly exhibit better performance. At  14 dB SNR, the intersection methods have RMSE
14 dB SNR, the intersection methods have RMSE  20 cm when reverberation time T60
20 cm when reverberation time T60  0.4 second. In contrast, the SRP- and MCCC-PHAT attain the same error with T60
0.4 second. In contrast, the SRP- and MCCC-PHAT attain the same error with T60  0.2 second.
0.2 second.
The results for talker location 2 are similar, except that there exists a systematic increase in RMS error. The decrease in performance is mainly caused by the slower convergence of the particle filter. At the start of the simulation, talker 1 becomes active and all of the particles are scattered randomly inside the room, according to the a priori distribution. When talker 2 becomes active and talker 1 silent, most of the particles are still at talker 1 location, and only a percent of the particles are scattered in the room. Therefore, the particle filter is more likely to converge faster to talker 1 than to talker 2, which is seen in the systematic increase of RMSE.
Evident in larger area of RMS error contour below 0.2 m multi- and Hamacher-PHAT increase the performance both in noisy and reverberant environments compared to SRP- and MCCC-PHAT.
7.3. Results for Real-Data Measurements
Since the location estimation process utilizes a stochastic method (PF), the calculations are repeated 500 times and then averaged. The averaged results are displayed for the four methods in Figure 8. The location estimates are plotted with a continuous line, and the active talker is marked with a dashed line. All methods converge to both speakers. The SRP-PHAT and MCCC-PHAT behave smoothly. The multi-PHAT and Hamacher-PHAT adapt to the switch of the active speaker more rapidly than other methods and also exhibit rapid movement of the estimator compared to the SRP- and MCCC-PHAT methods.
The RMS errors of the real-data segment are SRP-PHAT: 0.31 m, MCCC-PHAT: 0.29 m, Hamacher-PHAT: 0.14 m, and multi-PHAT: 0.14 m. The performance in the real-data scenario is further illustrated in Figure 9. The percentage of estimates outside a sphere centered at the ground truth location of both talkers is examined. The sphere radius is used as a threshold value to determine if an estimate is an outlier. The Hamacher-PHAT outperforms the others methods. SRP-PHAT has 80.6% of estimates inside the 25 cm error threshold, the MCCC-PHAT has 81.8%, the Hamacher-PHAT has 93.1%, and the multi-PHAT has 92.4%.
The marginal spatial likelihood functions from real-data recording are presented. The talker locations are marked with a square symbol (" "). The z-axis is the marginalized spatial likelihood over the whole conversation. In the RMSE sense (24), the likelihood mass is centered around the true position
"). The z-axis is the marginalized spatial likelihood over the whole conversation. In the RMSE sense (24), the likelihood mass is centered around the true position  in all cases.
in all cases.
The results agree with the simulations. The reason for the performance difference can be further examined by looking at the SLF shape. For this analysis, the SLFs are evaluated with a uniform grid of 5 cm density over the whole room area at three different elevations (0.95, 1.05, and 1.15 m). The marginal SLF is generated by integrating SLFs over the z-dimension and time. The normalized marginal spatial likelihood functions are displayed in Figure 10. In the RMSE sense (24), the likelihood mass is centered around the true position  in all cases. However, Hamacher- and multi-PHAT likelihood distributions have greater peakiness with more likelihood mass concentrated around the talker. The SRP-PHAT and MCCC-PHAT have a large evenly distributed likelihood mass, that is, large variance. Note that only a single talker was active at a time, and the marginal SLFs are multimodal due to integration over the whole recording time.
in all cases. However, Hamacher- and multi-PHAT likelihood distributions have greater peakiness with more likelihood mass concentrated around the talker. The SRP-PHAT and MCCC-PHAT have a large evenly distributed likelihood mass, that is, large variance. Note that only a single talker was active at a time, and the marginal SLFs are multimodal due to integration over the whole recording time.
8. Discussion
The simulations use the image method which simplifies the acoustic behavior of the room and source. The simulations neglect that the reflection coefficient is a function of the incident angle and frequency, and that the air itself absorbs sound [37]. The effect of the latter becomes more significant in large enclosures. The human talker is acoustically modeled as a point source. This simplification is valid for the simulations, since the data is generated using this assumption. In the real-data scenario, the sound does not originate from a single point in space, but rather from the whole mouth area of the speaker. Human speech is also directive, and the directivity increases at higher frequencies [37].
Due to the above facts, the simulation results presented here are not absolute performance values and can change when the system is applied in a real environment. However, the same exact simulation data was applied when comparing the methods. The results, therefore, give information about the relative performance of the methods under the simulation assumptions.
The methods were tested on a real recorded dialogue. All the methods were capable of determining the location of the sound source with varying accuracy. It is likely that the manual annotation and reference measurements contain some errors that affect the reported performance. The only difference between the methods was the way the spatial likelihood function was constructed from the pairwise microphone TDE functions. Since the intersection-based TDE combination methods have better variance, they offer more evidence for the sound source and therefore their convergence is also faster.
9. Conclusion
This article discusses a class of acoustic source localization (ASL) methods based on a two-step approach where first the measurement data is transformed using a time delay estimation (TDE) function and then combined to produce the spatial likelihood function (SLF). The SLF is used in a sequential Bayesian framework to obtain the source position estimate.
A general framework for combining the TDE functions to construct the SLF was presented. Combining the TDE functions using a union operation distributes more likelihood mass outside the source position compared to the intersection of TDE functions. The variance of the spatial likelihood distribution that is constructed with the intersection is thus lower. The particle filter converged faster with a low variance spatial likelihood function than a large variance likelihood function. This is evident in the simulation and real-data results.
Four different schemes to build the SLF from PHAT-weighted GCC values are implemented, specifically: multiplication, Hamacher  -norm (generalized multiplication), summation, and a determinant-based combination. The first two methods represent intersection, the summation represents union, and the determinant falls out of the presented TDE function categorization. In the experiments, the intersection methods gave the best results under different SNR and reverberation conditions using a particle filter. The location RMS error was reduced by 45% by preferring the intersection over the union when constructing the SLF.
-norm (generalized multiplication), summation, and a determinant-based combination. The first two methods represent intersection, the summation represents union, and the determinant falls out of the presented TDE function categorization. In the experiments, the intersection methods gave the best results under different SNR and reverberation conditions using a particle filter. The location RMS error was reduced by 45% by preferring the intersection over the union when constructing the SLF.
References
Stiefelhagen R, Garofolo J: Eval-ware: multimodal interaction. IEEE Signal Processing Magazine 2007,24(2):154-155.
Omologo M, Svaizer P: Use of the crosspower-spectrum phase in acoustic event location. IEEE Transactions on Speech and Audio Processing 1997,5(3):288-292. 10.1109/89.568735
Sheng X, Hu Y-H: Maximum likelihood multiple-source localization using acoustic energy measurements with wireless sensor networks. IEEE Transactions on Signal Processing 2005,53(1):44-53.
Doucet A, de Freitas N, Gordon N (Eds): Sequential Monte Carlo Methods in Practice, Statistics for Engineering and Information Science. Springer, New York, NY, USA; 2001.
Aarabi P: The fusion of distributed microphone arrays for sound localization. EURASIP Journal on Applied Signal Processing 2003,2003(4):338-347. 10.1155/S1110865703212014
Weiss A, Weinstein E: Fundamental limitations in passive time delay estimation—part 1: narrow-band systems. IEEE Transactions on Acoustics, Speech, and Signal Processing 1983,31(2):472-486. 10.1109/TASSP.1983.1164061
Champagne B, Bédard S, Stéphenne A: Performance of time-delay estimation in the presence of room reverberation. IEEE Transactions on Speech and Audio Processing 1996,4(2):148-152. 10.1109/89.486067
Gustafsson T, Rao BD, Trivedi M: Source localization in reverberant environments: modeling and statistical analysis. IEEE Transactions on Speech and Audio Processing 2003,11(6):791-803. 10.1109/TSA.2003.818027
Reed F, Feintuch P, Bershad N: Time delay estimation using the LMS adaptive filter—static behavior. IEEE Transactions on Acoustics, Speech, and Signal Processing 1981,29(3):561-571. 10.1109/TASSP.1981.1163614
Benesty J: Adaptive eigenvalue decomposition algorithm for passive acoustic source localization. Journal of the Acoustical Society of America 2000,107(1):384-391. 10.1121/1.428310
Chen J, Benesty J, Huang Y: Time delay estimation in room acoustic environments: an overview. EURASIP Journal on Applied Signal Processing 2006, 2006:-19.
Chen JC, Hudson RE, Yao K: A maximum-likelihood parametric approach to source localizations. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '01), May 2001, Salt Lake City, Utah, USA 5: 3013-3016.
Valin J-M, Michaud F, Rouat J: Robust localization and tracking of simultaneous moving sound sources using beamforming and particle filtering. Robotics and Autonomous Systems 2007,55(3):216-228. 10.1016/j.robot.2006.08.004
DiBiase J, Silverman HF, Brandstein M: Robust localization in reverberant rooms. In Microphone Arrays: Signal Processing Techniques and Applications. chapter 8, Springer, Berlin, Germany; 2001:157-180.
Lehmann EA: Particle filtering methods for acoustic source localisation and tracking,, Ph.D. dissertation. Australian National University, Canberra, Australia; 2004.
Korhonen T, Pertilä P: TUT acoustic source tracking system 2007. In Proceedings of the 2nd Annual International Evaluation Workshop on Classification of Events, Activities and Relationships (Clear '07), May 2007, Baltimore, Md, USA Edited by: Stiefelhagen R, Bowers R, Fiscus J.
Chen J, Benesty J, Huang Y: Time delay estimation using spatial correlation techniques. Proceedings of the 8th International Workshop Acoustic Echo and Noise Control (IWAENC '03), September 2003, Kyoto, Japan 207-210.
Ward DB, Lehmann EA, Williamson RC: Particle filtering algorithms for tracking an acoustic source in a reverberant environment. IEEE Transactions on Speech and Audio Processing 2003,11(6):826-836. 10.1109/TSA.2003.818112
Knapp C, Carter G: The generalized correlation method for estimation of time delay. IEEE Transactions on Acoustics, Speech, and Signal Processing 1976,24(4):320-327. 10.1109/TASSP.1976.1162830
Hassab J, Boucher R: Performance of the generalized cross correlator in the presence of a strong spectral peak in the signal. IEEE Transactions on Acoustics, Speech, and Signal Processing 1981,29(3):549-555. 10.1109/TASSP.1981.1163613
Chen J, Benesty J, Huang Y: Performance of GCC- and AMDF-based time-delay estimation in practical reverberant environments. EURASIP Journal on Applied Signal Processing 2005,2005(1):25-36. 10.1155/ASP.2005.25
Aarabi P, Mavandadi S: Robust sound localization using conditional time-frequency histograms. Information Fusion 2003,4(2):111-122. 10.1016/S1566-2535(03)00003-4
Jang J-S, Sun C-T, Mizutani E: Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence. chapter 2, Prentice-Hall, Upper Saddle River, NJ, USA; 1997.
Ash JN, Moses RL: Acoustic time delay estimation and sensor network self-localization: experimental results. Journal of the Acoustical Society of America 2005,118(2):841-850. 10.1121/1.1953307
Brutti A: Distributed microphone networks for sound source localization in smart rooms,, Ph.D. dissertation. DIT - University of Trento, Trento, Italy; 2007.
Do H, Silverman HF: A fast microphone array SRP-PHAT source location implementation using coarse-to-fine region contraction (CFRC). Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA '07), October 2007, New Paltz, NY, USA 295-298.
Do H, Silverman HF, Yu Y: A real-time SRP-PHAT source location implementation using stochastic region contraction(SRC) on a large-aperture microphone array. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 1: 121-124.
Dmochowski J, Benesty J, Affes S: A generalized steered response power method for computationally viable source localization. IEEE Transactions on Audio, Speech, and Language Processing 2007,15(8):2510-2526.
Zotkin DN, Duraiswami R: Accelerated speech source localization via a hierarchical search of steered response power. IEEE Transactions on Speech and Audio Processing 2004,12(5):499-508. 10.1109/TSA.2004.832990
Arulampalam S, Maskell S, Gordon N, Clapp T: A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Transactions on Signal Processing 2002,50(2):174-188. 10.1109/78.978374
Rife D, Vanderkooy J: Transfer-function measurement with maximum-length sequences. Journal of the Audio Engineering Society 1989,37(6):419-444.
Allen JB, Berkley DA: Image method for efficiently simulating small-room acoustics. Journal of the Acoustical Society of America 1979,65(4):943-950. 10.1121/1.382599
Schroeder MR: New method of measuring reverberation time. Journal of the Acoustical Society of America 1965,37(3):409-412. 10.1121/1.1909343
Hol J, Schön T, Gustafsson F: On resampling algorithms for particle filters. Proceedings of the Nonlinear Statistical Signal Processing Workshop, September 2006, Cambridge, UK 79-82.
Lehmann EA, Johansson AM, Nordholm S: Modeling of motion dynamics and its influence on the performance of a particle filter for acoustic speaker tracking. Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA '07), October 2007, New Paltz, NY, USA 98-101.
Lehmann EA, Johansson AM: Particle filter with integrated voice activity detection for acoustic source tracking. EURASIP Journal on Advances in Signal Processing 2007, 2007:-11.
Beranek L: Acoustics. American Institute of Physics, New York, NY, USA; 1986.
Acknowledgments
The authors wish to thank Dr. Eric Lehmann, for providing a simulation tool for the image method simulations, Sakari Tervo (M.S.) for assistance, Mikko Parviainen (M.S.), and the anonymous reviewers for their comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Pertilä, P., Korhonen, T. & Visa, A. Measurement Combination for Acoustic Source Localization in a Room Environment. J AUDIO SPEECH MUSIC PROC. 2008, 278185 (2008). https://doi.org/10.1155/2008/278185
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/278185


 -norm), product (
-norm), product ( -norm), and Hamacher
-norm), and Hamacher  -norm are illustrated along their resulting likelihoods. The contour lines represent constant values of output likelihood.Sum
-norm are illustrated along their resulting likelihoods. The contour lines represent constant values of output likelihood.Sum  Product
Product  Hamacher
Hamacher  -norm
-norm
 = SIR
= SIR  ;
; to
to
 do
do
 ;
;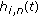 = RESAMPLE
= RESAMPLE  ;
;
 ], and they are identical in the simulations and in the real-data experiments.
], and they are identical in the simulations and in the real-data experiments.
 PF: PHAT-weighted GCC values are combined pairwise using the Hamacher
PF: PHAT-weighted GCC values are combined pairwise using the Hamacher 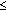 -norm (16), with parameter value
-norm (16), with parameter value  . The SIR-PF algorithm is then applied.
. The SIR-PF algorithm is then applied.



